Программный комплекс Locairheat [3] предназначен, в первую очередь, для проведения расчетов и подбора оборудования для обеспечения теплового режима помещений воздушно-отопительными агрегатами с учетом вязкости, турбулентности. Математическая модель, используемая в программе, включает в себя следующие уравнения: уравнение Навье-Стокса для несжимаемой жидкости в проекциях на оси x, y, z [5], уравнение неразрывности для несжимаемой жидкости [5], уравнение энергии для несжимаемой жидкости [7], уравнение Пуассона для давления, выведенное из уравнений движения и неразрывности [6].
Для учета турбулентности используется уравнение Рейнольдса [5; 7], которое внешне совпадает с уравнением Навье-Стокса [5], но записано для осредненных скоростей потока (![]() ), а также к кинематической вязкости добавляется турбулентная вязкость. В качестве модели турбулентности используется алгебраическая модель турбулентности Прандтля [7]
), а также к кинематической вязкости добавляется турбулентная вязкость. В качестве модели турбулентности используется алгебраическая модель турбулентности Прандтля [7]
![]() (1)
(1)
где ![]() – турбулентная вязкость;
– турбулентная вязкость; ![]() – эмпирический коэффициент, определяемый из эксперимента; b – ширина струи в рассматриваемом сечении;
– эмпирический коэффициент, определяемый из эксперимента; b – ширина струи в рассматриваемом сечении; ![]() – максимальная и минимальная осредненные скорости струи в рассматриваемом сечении.
– максимальная и минимальная осредненные скорости струи в рассматриваемом сечении.
Для использования названной алгебраической модели турбулентности необходимо определить эмпирический коэффициент ![]() . С данной целью был проведен лабораторный эксперимент по определению полей скоростей и температур местного воздушно-отопительного агрегата General мощностью 1,5 кВт. Расчетная сетка принята с шагами
. С данной целью был проведен лабораторный эксперимент по определению полей скоростей и температур местного воздушно-отопительного агрегата General мощностью 1,5 кВт. Расчетная сетка принята с шагами ![]() ,
, ![]() . Измеряемые параметры – скорость воздушного потока, м/с, температура воздушного потока, оС.
. Измеряемые параметры – скорость воздушного потока, м/с, температура воздушного потока, оС.
Измерительный прибор – термоанемометр Testo 425 (Германия). Диапазон измерений скорости 0…+20 м/с, температуры – -20…+70 оС. Данная модель измерительного прибора внесена в Государственный реестр средств измерений РФ.
На рис. 1 приведена схема установки для лабораторного эксперимента.
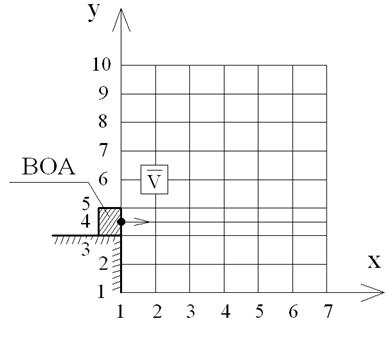
Рис. 1. Схема установки для лабораторного эксперимента
Измерялись параметры горизонтальной изотермической воздушной струи. На рис. 2 приведены результаты вычислительного эксперимента при различных значениях коэффициента ![]() , результаты лабораторного эксперимента (представлены значения скоростей изотермической воздушной струи в проекции на ось x при j=6).
, результаты лабораторного эксперимента (представлены значения скоростей изотермической воздушной струи в проекции на ось x при j=6).
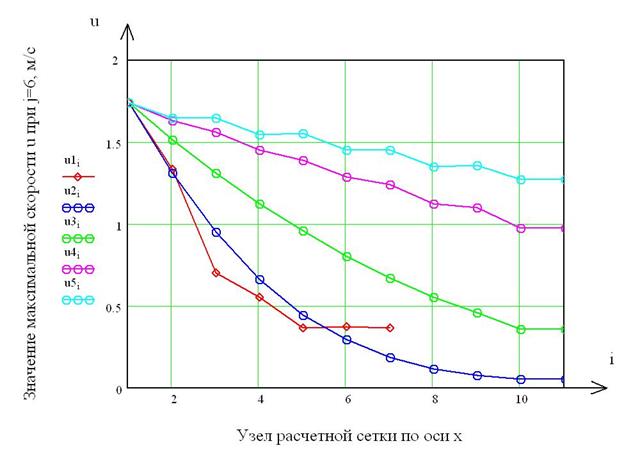
Рис. 2. u1 – данные, полученные при лабораторном исследовании;
u2 – расчет при ![]() ; u3 – расчет при
; u3 – расчет при ![]() ; u4 – расчет при
; u4 – расчет при ![]() ; u5 – расчет при
; u5 – расчет при ![]()
Для сравнения ниже приведены значения коэффициента ![]() в алгебраической модели турбулентности Прандтля для свободной турбулентной осесимметричной струи, принимаемые различными авторами:
в алгебраической модели турбулентности Прандтля для свободной турбулентной осесимметричной струи, принимаемые различными авторами:
– ![]() – Шубаэр, Чен [4];
– Шубаэр, Чен [4];
– ![]() – Шлихтинг [7];
– Шлихтинг [7];
– ![]() – Белов [1].
– Белов [1].
Сопоставление результатов вычислительных экспериментов и лабораторного эксперимента изменения скоростей изотермической воздушной струи в проекции на ось x при j=6 показало, что результаты вычислительного эксперимента в большей мере соответствуют результатам лабораторного эксперимента при значении эмпирического коэффициента ![]() .
.
Для проверки соответствия результатов вычислительных экспериментов, получаемых при применении разработанной расчетной программы Locairheat, реальным условиям применения воздушно-отопительных агрегатов был проведен натурный эксперимент. Эксперимент проводился на предприятии ОАО «Псковский хлебокомбинат». Исследовались параметры приточной нагретой воздушной струи от газового воздушно-отопительного агрегата марки Monzun фирмы Mandik с возможностью полной, частичной рециркуляции и прямотока.
Характеристики помещения и параметры приточной струи воздушно-отопительного агрегата (рис. 3):
1) размеры зоны помещения, обслуживаемой одним агрегатом, – 15x6x6 м (LxBxH);
2) ![]() – площадь воздухораспределительного устройства воздушно-отопительного агрегата;
– площадь воздухораспределительного устройства воздушно-отопительного агрегата;
3) ![]() – температура помещения;
– температура помещения;
4) ![]() – шаг по пространственной сетке;
– шаг по пространственной сетке;
5) ![]() – температура приточной струи;
– температура приточной струи;
6) ![]() – начальная скорость приточной струи;
– начальная скорость приточной струи;
7) потери тепла ![]() ;
;
8) способ подачи приточной струи – под углом 45о к горизонтальной оси агрегата.
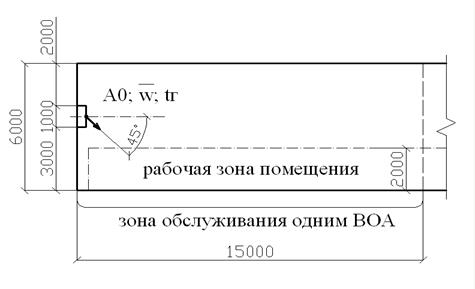
Рис. 3. Схема установки для натурного эксперимента
Скорости и температуры приточной струи измерялись термоанемометром Testo 425.
Результаты натурного и вычислительного экспериментов представлены на рис. 4.
Получены данные в натурном и вычислительном экспериментах по параметрам u (проекция вектора скорости на ось x) и T. Адекватность предложенной модели реальному процессу может быть подтверждена сопоставлением параметров процесса, полученных при вычислениях и в эксперименте. Проверка модели велась по значениям температур T.
Оценка адекватности предложенной теоретической модели экспериментальным данным выполнена с использованием F-критерия Фишера [2]. Для проверки адекватности сравниваются две дисперсии – общая дисперсия ![]() и остаточная дисперсия
и остаточная дисперсия ![]() (табл. 1):
(табл. 1):
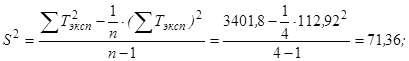 (2)
(2)
![]() (3)
(3)
Таблица 1
Вспомогательные данные для вычисления остаточной дисперсии
|
x |
Tэксп |
Tэксп2 |
Tрасч |
Tрасч2 |
Tэксп-Tрасч |
(Tэксп-Tрасч)2 |
|
1 |
40,04 |
1603,2 |
40,04 |
1603,2 |
0 |
0 |
|
2 |
28,13 |
791,3 |
28,29 |
800,3 |
-0,16 |
0,0256 |
|
3 |
24,11 |
581,3 |
24,88 |
619,0 |
-0,77 |
0,5929 |
|
4 |
20,64 |
426,0 |
23,14 |
535,5 |
-2,5 |
6,25 |
|
∑ |
112,92 |
3401,8 |
116,35 |
3558 |
-3,43 |
6,8685 |
а) 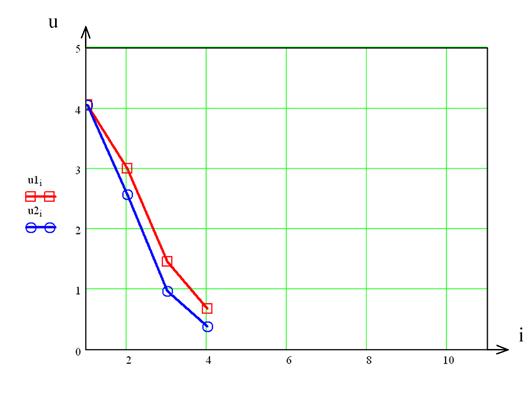
б) 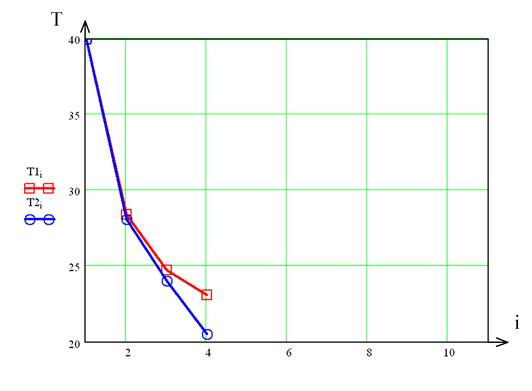
Рис. 4. Результаты натурного и вычислительного экспериментов изменения максимальной скорости, u, м/с, (а) и температуры, T, ºС, (б) на оси неизотермической воздушной струи:
u1, T1 – результаты натурного эксперимента; u2, T2 – результаты вычислительного эксперимента
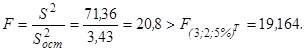 (4)
(4)
Для того чтобы численное решение адекватно описывало результаты экспериментов, необходимо, чтобы уравнения при 5%-ном уровне значимости описывали результаты опытов в 19,164 раза лучше среднего значения параметра (F(3; 2; 5 %)т = 19,164). Полученное фактическое значение (F = 20,8) превышает табличное значение, следовательно, численное решение статистически значимо описывает результаты экспериментов.
Выводы
1. Установлено, что результаты вычислительного эксперимента в большей мере соответствуют результатам лабораторного эксперимента при значении эмпирического коэффициента алгебраической модели турбулентности Прандтля ![]() .
.
2. Поскольку, согласно полученным результатам, численное решение статистически значимо описывает результаты экспериментов, разработанный программный комплекс Locairheat может применяться для выполнения вычислительных экспериментов, расчетов систем обеспечения температурного режима помещений воздушно-отопительными агрегатами.
Рецензенты:
Журавлев Ю.Н., д.т.н., профессор, Псковский государственный университет, г. Псков.
Плохов И.В., д.т.н., профессор, Псковский государственный университет, г. Псков.



