На крупных лесоперерабатывающих и целлюлозно-бумажных предприятиях для окорки древесины используется метод групповой окорки, осуществляемой в корообдирочных барабанах (КБ). КБ представляет собой полый вращающийся цилиндр, внутрь которого помещаются окариваемые лесоматериалы. На цилиндре секции крепятся бандажи, посредством которых они опираются на стальные опорные ролики с ребордами для восприятия осевых нагрузок. Корпуса подшипников роликов установлены на цельносварные рамы опорной станции, закрепленные на фундаменте. Работа КБ сопровождается значительными динамическими нагрузками и колебаниями, которые способствуют развитию деформаций и повреждений конструкции барабана, фундамента и снижению надежности, появлению осадок грунтовых оснований и нарушению работы КБ, а также в виде вибраций определенных частот оказывают неблагоприятное воздействие на людей. Поэтому для проектирования КБ необходимы данные о характеристиках динамических процессов, возникающих в конструкции барабана и фундаменте при окорке.
Целью настоящих исследований являлось определение амплитудно-частотных характеристик колебаний, возникающих в конструкции КБ и фундаменте при окорке лесоматериалов.
Для достижения поставленной цели решались следующие задачи.
- Разработка динамической модели системы КБ.
- Разработка математической модели колебаний системы КБ.
- Реализация математической модели в среде MathCad и выполнение имитационного моделирования процесса колебаний системы КБ для конкретного типоразмера барабана.
- Определение собственных частот колебаний фундамента КБ.
- Определение амплитудно-частотных характеристик колебаний системы «барабан-фундамент» на грунтовом основании.
- Обобщение модели для исследования КБ любого типоразмера.
При исследовании колебаний КБ фундамент и массив грунта под ним будем рассматривать как сложную систему, состоящую из нескольких упругих связанных между собой тел с распределенными параметрами. Известно, что модуль упругости бетона в сотни раз превышает модуль упругости грунта, поэтому фундамент можно считать абсолютно жестким, а сложную колебательную систему «барабан-фундамент» на грунтовом основании следует рассматривать как состоящую из нескольких упругих связанных между собой тел с распределенными параметрами. Для разработки динамической модели колебаний в фундаменте КБ примем модель грунтового основания Н.П. Павлюка – Э. Рауша с сосредоточенными параметрами [1; 2]. Фундамент по этой модели рассматривается как твердое тело, связанное с неподвижным основанием. Общий центр масс фундамента и КБ и центр тяжести подошвы фундамента лежат на одной вертикальной оси. Поэтому колебания фундамента можно разделить на ряд независимых колебаний: вертикальных, горизонтально–вращательных в двух взаимно перпендикулярных плоскостях и вращательных относительно вертикальной оси [1-3]. Силы, возбуждающие колебания фундаментов, действуют в вертикальном и горизонтально-поперечном направлениях. Поэтому рассмотрим колебания фундаментов также в этих направлениях. Пусть в некоторый момент времени фундамент из положения равновесия I переместится в положение II (рисунок 1).
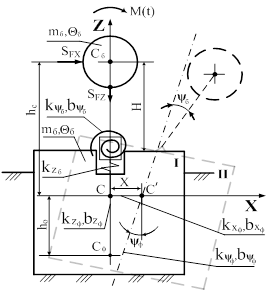
Рисунок 1 – Динамическая модель колебаний корообдирочного барабана на фундаменте
Движение фундамента определится значением трех независимых координат: проекциями Х и Y смещения центра масс фундамента и КБ на соответствующие координатные оси и углом поворота yф фундамента относительно оси, перпендикулярной плоскости колебаний. Движение барабана, кроме того, определяется углом поворота yб относительно фундамента.
Прикладывая к фундаменту и барабану силы и моменты сил, действующие на них в некоторый момент времени t, а также силы инерции и моменты сил инерции массы фундамента и барабана, проектируя их на оси X и Z и взяв сумму моментов всех сил относительно центра масс всей конструкции, а также сумму моментов всех сил, действующих на барабан относительно верхнего обреза фундамента, получим, согласно принципу Даламбера, систему дифференциальных уравнений:
; (1)
; (2)
; (3)
; (4)
, (5)
где 
,
- массы фундамента и барабана; 
,
- моменты инерции масс фундамента и барабана относительно центра масс системы; 
,
,
, 
,
,
- коэффициенты жесткости и неупругих сопротивлений грунта при вертикальных, горизонтальных и поворотных смещениях фундамента; kzб, 
,
,bzб - коэффициенты жесткости и неупругих сопротивлений опор барабана при вертикальных и горизонтально-вращательных смещениях барабана; 
- расстояние от центра масс установки до центра жесткости основания по вертикали; 
- расстояние от центра масс установки до центра масс барабана; 
- расстояние от верхнего обреза фундамента до центра масс барабана; 
- амплитуды i–х гармонических составляющих возмущающегося момента; 
, 
, 
- углы сдвига фаз гармонических составляющих сил и момента; 
, 
- спектральная плотность ударной нагрузки при отрыве бревен от стенки барабана и их ударе в вертикальном и горизонтальном направлении.
Уравнения (1, 2) независимы от уравнений (3-5), которые являются взаимосвязанными. Следовательно, вертикальные колебания можно рассматривать независимо от горизонтальных и вращательных колебаний.
Приравняв к нулю неупругие сопротивления и возмущающие силы в уравнениях (1-5), описывающие вертикальные и горизонтально-вращательные колебания фундамента КБ, из преобразованной таким образом системы уравнений определяются собственные частоты колебаний конструкции.
Реализация математической модели (1-5) была выполнена в среде MathCad. Как показали расчеты, собственные частоты колебаний системы для барабана марки КБ-425 с размерами фундамента аф=7,8 м, bф=25,7 и с учетом коэффициента с0=14 МН/м3 для естественных оснований фундаментов машин [3], соответствующих грунту в виде мелкозернистого водонасыщенного песка рыхлой и средней плотности, составили: вертикальных колебаний f1бф = 11,5 Гц и f2бф = 26,6Гц; горизонтально-вращательных f1гх = 9,2 Гц и f2гy = 10,3 Гц и f1гф = 48,1 Гц.
Низшие собственные частоты вертикальных и горизонтально–вращательных колебаний фундамента близки к собственным частотам крутильно–вращательных колебаний привода, субгармонике открытой зубчатой передачи и частоте вращения двигателя [4; 5]. При совпадении этих частот амплитуды колебаний на низших собственных частотах вертикальных и горизонтально–вращательных колебаний фундамента возрастут.
Исследования амплитудно-частотных характеристик системы выполнялись методом моделирования по следующей методике.
Решение уравнений (1, 2), описывающих вынужденные вертикальные колебания фундамента, ищем в виде:
; 
(6)
Решение уравнений (3-5), описывающих вынужденные горизонтально-вращательные колебания, ищем в виде:
; 
;
. (7)
Амплитуда горизонтально–вращательных колебаний фундамента КБ-425 на уровне корпусов подшипников опорных роликов складывается из горизонтальных и вращательных колебаний фундамента КБ на этом же уровне и выражается зависимостью
, (8)
где hп1, hп2 – расстояние от центра масс фундамента и барабана соответственно до корпусов подшипников опорных роликов.
Подставляя решения уравнений (6) в уравнения (1, 2), а решения уравнения (7) в уравнения (3-5), с учетом (8) получим после преобразований систему линейных алгебраических уравнений, описывающих вынужденные вертикальные и горизонтально-вращательные колебания системы «барабан–фундамент» на грунтовом основании. Система уравнений реализована в среде MathCad, а на рисунке 2 в формате MathCad показаны результаты расчетов амплитудно-частотных характеристик вертикальных и горизонтально–вращательных колебаний системы «барабан–фундамент» на грунтовом основании для барабана КБ-425.
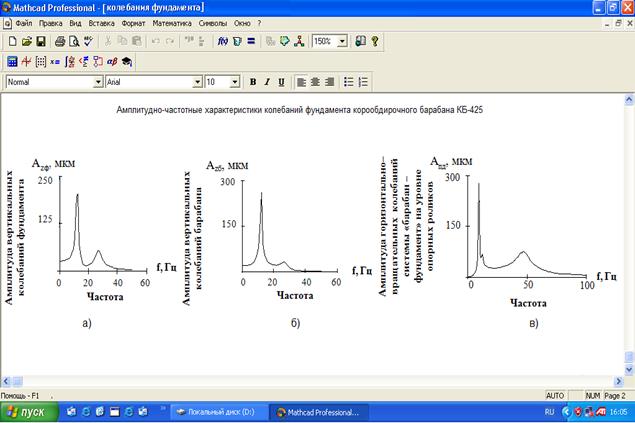
Рисунок 2 – Амплитудно-частотные характеристики колебаний системы «барабан–фундамент» на грунтовом основании в среде MathCad барабана КБ-425: а – вертикальные колебания фундамента; б – вертикальные колебания КБ;в – горизонтально–вращательные колебания КБ на уровне подшипниковых опор
Из рисунка 2 следует, что собственные частоты колебаний фундамента и частоты, на которых проявляются пики, совпадают. Это является одним из подтверждений адекватности принятой модели.
Корообдирочные барабаны серии КБ, выпускаемые ЗАО «Петрозаводскмаш», являются конструктивно подобными. Такими же конструктивно подобными предусмотрены для них и фундаменты. В различных по габаритам барабанах обрабатывается одинаковая по размерно-качественным характеристикам древесина, поэтому уравнения (1-5) применимы и ко всей группе барабанов. Зная исходные данные в уравнениях (1-5), можно определить динамические характеристики системы «барабан-фундамент» на грунтовом основании любых подобных КБ на фундаменте, что позволит использовать предложенные модели на стадии проектирования. Исходя из вышесказанного, можно обобщить модель, проверенную на адекватность на примере КБ-425, для всех типоразмеров барабанов конструктивного ряда.
Выводы
На основании проведенных исследований можно сделать следующие выводы.
- Разработанные динамическая (рисунок 1) и математическая (1-5) модели системы «барабан-фундамент» на грунтовом основании достаточно корректно и точно описывают колебания в элементах конструкции КБ и его фундамента. Реализация моделей в компьютерной программе MathCad позволяет использовать в практике проектирования барабанов и фундаментов для выполнения имитационного моделирования их колебаний.
- Определены собственные частоты колебаний конструкции КБ и фундамента.
- Получены амплитудно–частотные характеристики системы по всем обобщенным координатам.
- На примере исследования барабана КБ-425 показана достаточная адекватность модели, а также обобщены результаты исследования с возможностью использования для барабанов любого типоразмера.
Рецензенты:
Гороховский Александр Григорьевич, доктор технических наук, профессор, генеральный директор ОАО «Уральский научно-исследовательский институт переработки древесины», г. Екатеринбург.
Баженов Евгений Евгеньевич, доктор технических наук, профессор, директор института автомобильного транспорта и технологических систем ФГБОУ ВПО «УГЛТУ», г. Екатеринбург.