Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Для передачи и распределения электрической энергии на электрических станциях, подстанциях и промышленных предприятиях широко применяются различные шинопроводы со сплошными шинами прямоугольного сечения согласно рисунку.

При проектировании таких шинопроводов и подключенного к ним электрооборудования необходимо знать в установившемся режиме при синусоидальном токе такие параметры шин как сопротивление R0 (Ом/м) и внутреннюю индуктивность L0 (Гн/м), коэффициент теплообмена [Вт/(м2·°С)] с окружающей средой поверхности шин при их заданной температуре (°С) и известной температуре окружающей среды (°С), которые должны находиться с учетом магнитной проницаемости (Гн/м) и удельной проводимости γ (1/Ом·м) материала шины, частоты f (Гц) синусоидального тока и поверхностного эффекта в шине [3–5]. Поэтому разработка методики расчета параметров прямоугольных шин с учетом поверхностного эффекта представляется актуальной задачей. В данной статье предложена методика, полученная на основе уравнений электромагнитного поля, которые программируются в среде Mathcad [1] для автоматизированного инженерного расчета параметров прямоугольных шин.

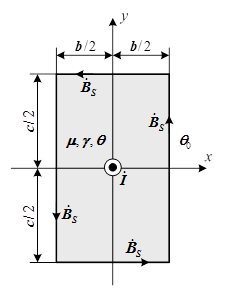
Рисунок. Прямоугольная шина с комплексом действующего значения тока , направленного «к нам» по оси z: – магнитная проницаемость и удельная проводимость материала шины; – температура шины и окружающей среды соответственно; – комплекс действующего значения индукции на поверхности шины; – размеры шины

Сопротивления и индуктивности шин при постоянном и синусоидальном токе с учетом частоты, удельной проводимости материала шин и поверхностного эффекта могут быть найдены при помощи программы компьютерного моделирования Elcut [2]. Однако отсутствие расчетных формул и необходимость моделирования для каждой конкретной шины затрудняют анализ большого числа вариантов и ограничивают применение программы Elcut при инженерных расчетах. Поэтому разработка методики расчета параметров прямоугольных шин на основе уравнений и законов электромагнитного поля актуальна и является предметом рассмотрения в настоящей работе.

Допущения

Для получения расчетных формул сделаем следующие допущения.

1. Рассчитываемый коэффициент теплообмена поверхности шины с окружающей средой определяется условиями теплоотвода благодаря естественной или вынужденной конвекции, а также теплоизлучению [5].

2. Вся толща шины характеризуется постоянными значениями магнитной проницаемости , температуры и удельной проводимости , причем [5]:

, (1)

где – удельная проводимость шин при температуре окружающей среды ;

– постоянный температурный коэффициент (1/°С).

3. Растекание тока вдоль шины (краевой эффект) учитывать не будем, считая при этом, что площадь поперечного сечения шины (м2) и её внешний периметр (м) постоянны.

4. Будем исходить из представления о двух одномерных электромагнитных волнах [3, 4], проникающих в шину перпендикулярно её поверхности вдоль осей x и y согласно рисунку.

5. Комплекс действующего значения индукции на поверхности шины постоянен и определяется по закону полного тока в комплексной форме [3, 4]:

. (2)

Методика расчета

Составляющие магнитной индукции переменного электромагнитного поля и плотность тока в шине () будем рассчитывать в функциях координат x и y согласно рисунку по следующим уравнениям в комплексной форме [3, 4]:

; (3)

; (4)

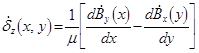, (5)

где – комплексы действующих значений проекций вектора магнитной индукции на оси x и y соответственно;

– комплекс действующего значения плотности тока в шине, совпадающий по направлению с осью z и направлен «к нам»;

– угловая частота тока и электромагнитного поля;

– мнимая единица.

С учетом граничного условия на поверхности шины, приведенного на рисунке, решением уравнений (3–5) будут следующие функции и константы электромагнитного поля:

; (6)

; (7)

; (8)

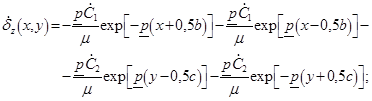(9)

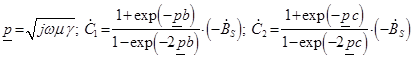, (10)

где – модуль действующего значения вектора магнитной индукции.

Сопротивление шины (Ом/м) найдем на основе закона Джоуля-Ленца в дифференциальной форме [3, 4] и плотности тока (9):

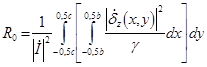, (11)

а внутреннюю индуктивность шины (Гн/м) определим, исходя из запасенной магнитной энергии [3, 4] и индукции (8):

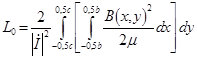. (12)

Для определения необходимого коэффициента теплообмена при заданных температурах шины и окружающей среды воспользуемся уравнением теплового баланса для шины [5]:

,

тогда

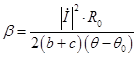. (13)

Результаты расчета

По запрограммированным в среде Mathcad [1] формулам (1–13) и по программе Elcut [2] были проведены расчеты параметров шин. В таблицах 1–5 приведены результаты этих расчетов при частотах f=50; 100; 200; 400 (Гц) и токе (кА) для медных, алюминиевых и железных шин [5, 6] при одинаковой площади поперечного сечения (мм2).

Таблица 1

Исходные параметры шин при (°С) и (Гн/м)

Таблица 2

Расчетные параметры медных шин

Таблица 3

Расчетные параметры алюминиевых шин

Заключение

1. Предложенная методика расчета позволяет определять такие параметры прямоугольных шин в установившемся режиме при синусоидальном токе как сопротивление, внутреннюю индуктивность и коэффициент теплообмена, которые рассчитываются с учетом поверхностного эффекта, частоты синусоидального тока, материала шин, их температуры и температуры окружающей среды.

2. Разработанная методика получена на основе уравнений электромагнитного поля, которые могут быть запрограммированы, например, в среде Mathcad для автоматизированного инженерного расчета параметров прямоугольных шин.

3. С увеличением частоты тока возрастают сопротивление и коэффициент теплообмена при уменьшении внутренней индуктивности шины. При увеличении удельной проводимости материала шины уменьшаются сопротивление и внутренняя индуктивность. С увеличением магнитной проницаемости возрастают: сопротивление, внутренняя индуктивность и коэффициент теплообмена. Для более плоских шин сопротивление, внутренняя индуктивность и коэффициент теплообмена меньше, чем для шин с квадратным сечением.

Таблица 4

Расчетные параметры железных шин при =10

4. Достоверность методики подтверждается удовлетворительным совпадением результатов расчета сопротивления и индуктивности с результатами, полученными при помощи программы компьютерного моделирования Elcut.

Таблица 5

Расчетные параметры железных шин при =100

Работа выполнена в рамках государственного задания «Наука» 7.2826.2011 «Разработка и создание гибридной модели энергоблоков электростанций».

Рецензенты:

Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО НИ ТПУ, Национальный исследовательский Томский политехнический университет, г.Томск.

Канев Ф.Ю., д.ф.-м.н., ведущий научный сотрудник института оптики атмосферы им. В. Е. Зуева СО РАН, г. Томск.