Информационно-аналитические системы (ИАС) предназначены для решения задач принятия решений при управлении на основе данных, получаемых в процессе производственной, образовательной или коммерческой деятельности. Комплекс ИАС предприятия или организации может затрагивать всю управленческую вертикаль: корпоративную отчетность, финансово-экономическое и стратегическое планирование. При этом ИАС являются надстройкой над уже функционирующими информационными приложениями и не требуют их замены [2]. В ИАС аккумулируются данные по различным видам деятельности, включая состояния производственной или финансовой деятельности. Как правило, ИАС подразделений предполагают более углубленную детализацию и сложную аналитическую обработку данных.
В процессе проектирования любая ИАС может рассматриваться как четверка ![]() , где
, где ![]() – множество объектов,
– множество объектов, ![]() – множество свойств (атрибутов),
– множество свойств (атрибутов), ![]() – множество всех возможных значений свойств, а
– множество всех возможных значений свойств, а ![]() – информационная функция [5]. При этом разработка модельного представления проблемно-ориентированной ИАС может выполняться как с использованием исчисления предикатов, так и тензорного исчисления [1, 4].
– информационная функция [5]. При этом разработка модельного представления проблемно-ориентированной ИАС может выполняться как с использованием исчисления предикатов, так и тензорного исчисления [1, 4].
Тензорное исчисление эффективно в различных областях деятельности: гидромеханика, электротехника, системы массового обслуживания и телекоммуникационные системы. Поскольку большинство тензоров описываются с помощью многомерных массивов [1], такое же представление имеют таблицы баз и хранилищ данных, было решено использовать аппарат тензорной алгебры для формализованного описания многомерного пространства данных ИАС. Существует ряд предпосылок для применения тензорного исчисления при формализованном описании моделей данных:
- классы реальных объектов предметной области ИАС представляются в виде отдельных сущностей (таблиц);
- формализованное описание объектов осуществляется с учетом заданной системы измерений предметной области (координат).
- преобразование объекта при переходе из одной системы координат в другую выполняется с учетом выполнения требований аксиом Армстронга.
- наличие в модельном представлении данных инвариантов – параметров, значения которых не меняются при переходе из одной системы координат в другую.
Одной из основных частей ИАС является средства хранения данных, состоящие из транзакционных баз данных (БД) и хранилищ данных (ХД). Предположим, что модель фрагмента БД приведена на рисунке 1. В соответствии с этой моделью сущность «Запись» отражает значения показателей деятельности аспирантов за определенный период времени.
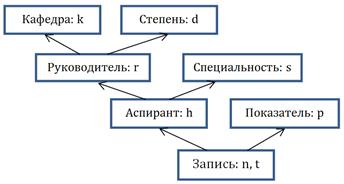
Рисунок 1. Модель данных «Снежинка»
На основе тензорной методологии, развитой в работах Г. Крона, любую структуру многомерного пространства данных или базис пространства можно задать в виде индексного объекта второй валентности [3]. Базис пространства модели данных «Снежинка», представленной на рисунке 1, можно задать в виде квадратной матрицы, описывающей индексный объект со скользящими индексами ![]() , на верхнем (системном) уровне модельного представления:
, на верхнем (системном) уровне модельного представления:

Индексный объект ![]() представляет собой выбранный базис предметного пространства данных «Снежинка» с размерностью равной семи, определяемой количеством измерений. Для детального описания всех объектов рассматриваемого многомерного предметного пространства (сущностей) вводим набор фиксированных индексов:
представляет собой выбранный базис предметного пространства данных «Снежинка» с размерностью равной семи, определяемой количеством измерений. Для детального описания всех объектов рассматриваемого многомерного предметного пространства (сущностей) вводим набор фиксированных индексов: ![]() . В этом случае любой объект модели можно представить в многомерном пространстве в виде индексного объекта первой валентности, содержащего набор фиксированных индексов и один скользящий индекс. Наличие первичного ключа задается единицей со знаком «+», наличие внешнего ключа – единицей со знаком «-». Например, класс «Аспирант» модели данных можно представить как индексный объект:
. В этом случае любой объект модели можно представить в многомерном пространстве в виде индексного объекта первой валентности, содержащего набор фиксированных индексов и один скользящий индекс. Наличие первичного ключа задается единицей со знаком «+», наличие внешнего ключа – единицей со знаком «-». Например, класс «Аспирант» модели данных можно представить как индексный объект:
![]() . (1)
. (1)
Поскольку в выражении (1) скользящие индексы ![]() имеют нулевое значение, то возможно использование сокращенной записи индексного объекта
имеют нулевое значение, то возможно использование сокращенной записи индексного объекта ![]() . В этой записи нижний фиксированный индекс соответствует первичному ключу, верхние фиксированные индексы соответствуют внешним ключам.
. В этой записи нижний фиксированный индекс соответствует первичному ключу, верхние фиксированные индексы соответствуют внешним ключам.
С использованием рассмотренных представлений индексных объектов может быть решена задача преобразования базисов пространств. Зададим базис многомерного пространства, определяемого моделью данных «Звезда», приведенной на рисунке 2.
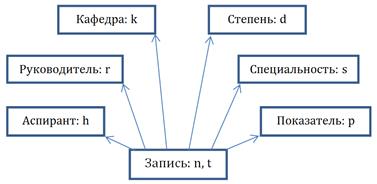
Рисунок 2 – Модель данных «Звезда»
В соответствии с рисунком 2 базис многомерного пространства имеет вид:

Для заданных базисов ![]() ,
, ![]() многомерных пространств можно задать преобразования следующего вида:
многомерных пространств можно задать преобразования следующего вида:
![]() или
или ![]() ,
,
где ![]() – тензор преобразования базы пространства данных «Снежинка» в базу пространства «Звезда» с валентность равной двум.
– тензор преобразования базы пространства данных «Снежинка» в базу пространства «Звезда» с валентность равной двум.
Применение индексных объектов позволяет производить анализ структур данных. Для этого необходимо определить инварианты в пространствах данных:
- объем данных для описания одного и того же набора измерений в различных предметных пространствах фиксировано;
- объем данных, хранимых в таблицах мер различных предметных пространств, без учета структуры функциональных зависимостей неизменно.
Определение инвариантов позволяет осуществлять расчет объема хранимой информации при любой структуре и выполнять преобразование одной структуры данных в другую без потери данных. Расчет объема хранимой информации производится в два этапа.
На первом этапе выполняется анализ структуры модели данных, содержащей сущности без указания внешних зависимостей (рисунок 3).

Рисунок 3. Модель данных ![]() без внешних связей
без внешних связей
В модели на рисунке 3 использованы следующие обозначения: ![]() – количество записей в сущностях,
– количество записей в сущностях, ![]() – размерность экземпляра сущности в атрибутах. В соответствии с базисом пространства, в котором представлена модель
– размерность экземпляра сущности в атрибутах. В соответствии с базисом пространства, в котором представлена модель ![]() , расчет хранимой информации с учетом количества записей и размерности экземпляра сущности может быть выполнен с использованием выражения:
, расчет хранимой информации с учетом количества записей и размерности экземпляра сущности может быть выполнен с использованием выражения:
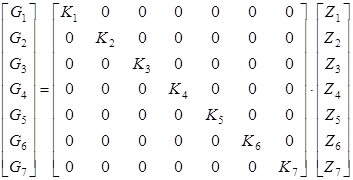 .
.
При этом, объем хранимой информации, измеряемый в атрибутах, будет рассчитываться по формуле:
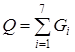 . (2)
. (2)
На втором этапе осуществляется анализа структуры данных при выявленных функциональных зависимостях ![]()
![]() ,
, ![]()
![]()
![]()
![]() и ограничении уровня иерархии измерений, равном 2. В этом случае модель структуры данных имеет вид, приведенный на рисунке 4.
и ограничении уровня иерархии измерений, равном 2. В этом случае модель структуры данных имеет вид, приведенный на рисунке 4.
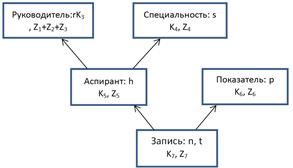
Рисунок 4. Модель с ограничением уровня иерархии измерений
Как видно из рисунка, базис пространства был преобразован. В модели, убрав один уровень иерархии, а функциональные зависимости, заданные в модели данных «Снежинка» (рисунок 1), сохранены. В этом случае базис пространства имеет вид:
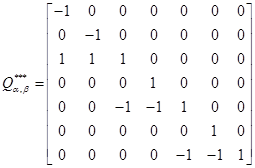
На втором этапе также определяется объем данных, необходимый для представления внешних ключей. Предположим, что для рассматриваемой модели объемы данных для представления внешних ключей имеют следующие значения:
![]()
![]()
![]()
![]()
![]()
Таким образом, объем хранимой информации в каждой сущности модели с учетом внешних связей можно рассчитать по следующей формуле:
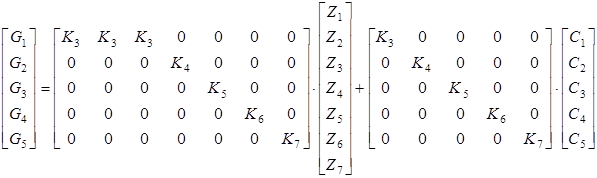
Объем данных, хранимых во всей БД, рассчитывается по формуле (2).
Рассмотрим пример расчета объема данных при следующих начальных данных:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Объем хранимых данных при структуре, представленной на рисунке 4, равен:
![]() ,
,
а при структуре со всеми уровнями иерархии измерений (рисунок 1):
![]() .
.
Следовательно, если убрать один уровень иерархии измерений в структуре данных, то объем хранимых данных увеличится на 21 %. Такие вычисления целесообразно производить при выборе оптимальной структуры хранилища или базы данных, подборе технологической платформы реализации выбранной структуры, поскольку некоторые аналитические платформы (например, Deductor Studio компании BaseGroup Labs) поддерживают только два уровня иерархии.
Таким образом, введение понятия базиса многомерного пространства данных, задание базисов пространства и классов объектов в виде индексных объектов, определение инвариантов реляционных моделей данных существенно расширяют применение тензорной методологии при проектировании баз и хранилищ данных ИАС. Дальнейшее развитие тензорной методологии применительно к информационным системам связано с решением задачи анализа процессов сбора, предварительной обработки, оперативного и интеллектуального анализа данных в ИАС.
Рецензенты:
Зинкин С. А. д.т.н., профессор, профессор кафедры «Вычислительная техника» Пензенского государственного университета, г. Пенза.
Макарычев П. П. д.т.н., профессор, зав. кафедрой «Математическое обеспечение и применение ЭВМ» Пензенского государственного университета, г. Пенза.



