Введение
В настоящее время во всем мире активно используется метод лечебной физкультуры, основанный на выполнении дозированных движений, осуществляемых с помощью механотерапевтических аппаратов, облегчающих движения или, наоборот, требующих дополнительных усилий для их выполнения. Этот метод называется «Механотерапия», и он предназначается для избирательного воздействия на определённые функции двигательной системы человека [2; 8].
Зачастую травма и вынужденная обездвиженность приводят к частичной атрофии мышц и связочного аппарата. Сращение кости, позволяющее приступить к полноценным нагрузкам, происходит от одного до шести месяцев в зависимости от тяжести и локализации травмы, а полноценное восстановление связочно-мышечного аппарата происходит гораздо позже, чем сращение костей или поврежденных связок. Если опорно-двигательный аппарат не подвергается каким-либо нагрузкам, то процессы разрушения начинают преобладать над процессами восстановления, что и происходит одномоментно после травмы [3].
Поэтому реабилитация после травмы даже при идеальном первичном лечении необходима для максимального ускорения восстановления.
Важно понимать, что реабилитация конечностей или суставов решает две основные проблемы: восстановление полного объема движений в суставе и наращивание мышечной силы и массы; восстановление правильного стереотипа движений [5].
Одним из главных направлений в реабилитации является разработка суставов. Существует большое количество различных тренажеров, методик и реабилитационных систем, которые позволяют заниматься реабилитацией конечностей, при этом управление аппаратами для разработки суставов максимально упрощено и не требует специальных знаний [6; 7]. В настоящее время наибольшее распространение получили двухзвенные системы с одним активным шарниром. Такие устройства имеют ограниченные функциональные возможности, с целью их расширения появились трехзвенные конструкции аппаратов с несколькими активными шарнирами. Трехзвенная система может иметь пассивный коленный шарнир, а голеностопный шарнир перемещаться поступательно.
В большинстве случаев тренажеры представляют собой системы для пассивной реабилитации, которые лишь сгибают и разгибают сустав в пределах заданного угла. При этом недостаточное внимание уделяется разработке и исследованию аппаратов, воздействующих на нужные группы мышц в определенные фазы движения сустава, тем самым навязывается правильный стереотип ходьбы и тренируются мышцы, необходимые для правильной походки. В данной статье рассматривается исследование заданного движения трехзвенного механизма с активными тазобедренным, коленным и голеностопным суставами, работа которого осуществляется в сопряжении с основными принципами движения нижней конечности человека. Применение таких активных элементов существенно повышает эффективность реабилитационных мероприятий.
Целью данного исследования является изучение закономерностей управляемого движения трехзвенного механизма с тремя активными шарнирами. Для достижения поставленной цели необходимо разработать математическую модель движения трехзвенника, получить результаты исследования матмодели, провести сравнительный анализ с экспериментальными данными.
Описание трехзвенного механизма
В работе рассматривается трехзвенный механизм, звенья 1-3 которого соединены между собой приводами вращательного движения 4-6. Положение звеньев определяется углами ![]() ,
, ![]() ,
, ![]() . Со стороны корпуса на звено 1 действует момент
. Со стороны корпуса на звено 1 действует момент ![]() , со стороны звена 1 на звено 2 действует момент
, со стороны звена 1 на звено 2 действует момент ![]() , со стороны звена 2 на звено 1 действует момент
, со стороны звена 2 на звено 1 действует момент![]() , со стороны звена 2 на звено 3 действует момент
, со стороны звена 2 на звено 3 действует момент![]() , и со стороны звена 3, в свою очередь, на звено 2 действует момент
, и со стороны звена 3, в свою очередь, на звено 2 действует момент ![]() . Кроме того, на звенья механизма действуют силы веса, которые в общем случае направлены под некоторым углом α к выбранной системе координат, что отражает возможность устройства проводить реабилитационные мероприятия в различных плоскостях, например в горизонтальной и вертикальной.
. Кроме того, на звенья механизма действуют силы веса, которые в общем случае направлены под некоторым углом α к выбранной системе координат, что отражает возможность устройства проводить реабилитационные мероприятия в различных плоскостях, например в горизонтальной и вертикальной.
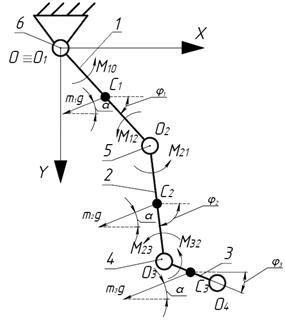
Рис. 1. Расчетная схема трехзвенного механизма
Рассмотрим движение трехзвенника, при котором ось привода 6 остается неизменной. Пусть в начальном положении звенья 1, 2 и 3 находятся под углами ![]() ,
, ![]() и
и ![]() . Звено 1 совершает вращательное движение под действием системы моментов, и его положение в любой момент времени определяется углом
. Звено 1 совершает вращательное движение под действием системы моментов, и его положение в любой момент времени определяется углом ![]() , при этом на протяжении движения звена 1 звено 2 совершает плоско-параллельное движение, вращательная составляющая которого задается углом
, при этом на протяжении движения звена 1 звено 2 совершает плоско-параллельное движение, вращательная составляющая которого задается углом ![]() , звено 3 движется так же плоско-параллельно, и его вращение задается углом
, звено 3 движется так же плоско-параллельно, и его вращение задается углом ![]() .
.
Математическое моделирование движения трехзвенного механизма
При разработке математической модели использовались следующие допущения: все звенья механизма являются абсолютно твердыми, недеформируемыми телами, которые моделируются стержнями с равномерно распределенной массой, центры масс ![]() ,
, ![]() ,
, ![]() совпадают с геометрическими центрами звеньев 1-3.
совпадают с геометрическими центрами звеньев 1-3.
Рассмотрим многозвенник ![]() ,
, ![]() ,
, ![]() ,
, ![]() , лежащий на координатной плоскости OXY (рис. 1). Он состоит из трех звеньев с центрами масс в точках
, лежащий на координатной плоскости OXY (рис. 1). Он состоит из трех звеньев с центрами масс в точках ![]() ,
, ![]() ,
, ![]() . Рассматривается плоское движение системы. На звенья системы наложены стационарные голономные связи, поэтому число степеней свободы совпадает с числом обобщенных координат.
. Рассматривается плоское движение системы. На звенья системы наложены стационарные голономные связи, поэтому число степеней свободы совпадает с числом обобщенных координат.
В качестве обобщенных координат будем рассматривать углы поворота ![]() ,
, ![]() ,
, ![]() каждого из звеньев относительно их центров масс. Получаем следующий вектор обобщенных координат:
каждого из звеньев относительно их центров масс. Получаем следующий вектор обобщенных координат:
![]()
Геометрические связи, наложенные на механическую систему, представим в виде:
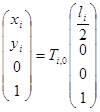 ; (1)
; (1)
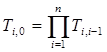 ; (2)
; (2)
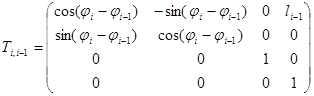 ; (3)
; (3)
i - номер звена;![]() - абсолютный угол наклона i-го звена к оси
- абсолютный угол наклона i-го звена к оси ![]() ;
; ![]() ,
, ![]() ; - координаты центров масс i-го звена в абсолютной системе координат
; - координаты центров масс i-го звена в абсолютной системе координат ![]() .
.
Для звена ![]() :
: ![]() ,
,![]() . Векторы скоростей центров масс
. Векторы скоростей центров масс ![]() ,
, ![]() ,
, ![]() звеньев имеют следующий вид:
звеньев имеют следующий вид:
![]() , где (4)
, где (4)
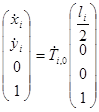 , где (5)
, где (5)
Для получения дифференциальных уравнений движения данной системы воспользуемся уравнениями Лагранжа 2-го рода в форме:
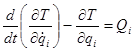 , где (6)
, где (6)
Т – кинетическая энергия всей системы;
![]() , где (7)
, где (7)
n - число звеньев.
Так как все звенья рассматриваемой системы совершают плоское движение, кинетическая энергия каждого звена будет складываться из кинетической энергии вращательного и поступательного движения:
![]()
![]() ; (8)
; (8)
![]() - угловая скорость i-го звена системы.
- угловая скорость i-го звена системы.
Модуль векторов скоростей:
![]() (9)
(9)
Центральные моменты инерции звеньев будем вычислять по формуле:
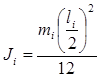 ; (10)
; (10)
![]() - масса i-го звена системы.
- масса i-го звена системы.
Для определения обобщенных сил ![]() воспользуемся принципом возможных перемещений. Сообщим системе виртуальное перемещение
воспользуемся принципом возможных перемещений. Сообщим системе виртуальное перемещение ![]() и найдем на нем работу всех сил и моментов, приложенных к системе на каждом этапе движения трехзвенника.
и найдем на нем работу всех сил и моментов, приложенных к системе на каждом этапе движения трехзвенника.
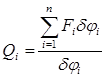 (11)
(11)
Подставляя (7), (10) в (5), с учетом (8), (9) после соответствующих преобразований получим систему дифференциальных уравнений, описывающих движение рассматриваемого механизма:
 (12)
(12)
Результаты математического моделирования
Будем решать задачу определения закономерностей движения (зависимости изменения углов звеньев, угловых скоростей, ускорений точек ![]() от времени) трехзвенника с тремя активными шарнирами
от времени) трехзвенника с тремя активными шарнирами ![]() ,
, ![]() ,
, ![]() для заданных управляющих воздействий
для заданных управляющих воздействий ![]() .
.
Экспериментально были определены зависимости управляющих моментов от времени (рис. 2).
а)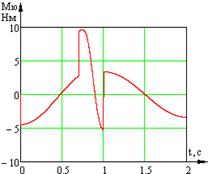 б)
б)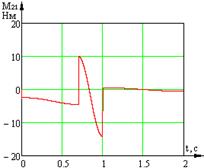 в)
в)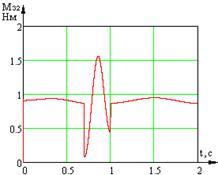
Рис. 2. Временные характеристики изменения моментов звеньев системы:
а) временная характеристика изменения момента ![]() звена 1; б) временная характеристика изменения момента
звена 1; б) временная характеристика изменения момента ![]() звена 2; в) временная характеристика изменения момента
звена 2; в) временная характеристика изменения момента ![]() звена 3
звена 3
Получим диаграммы изменения углов, угловых скоростей, ускорений звеньев трехзвенника.
а)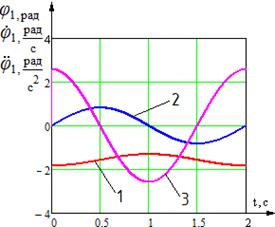 б)
б)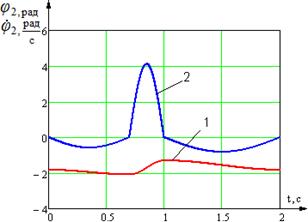
в)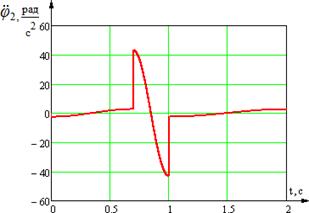 г)
г)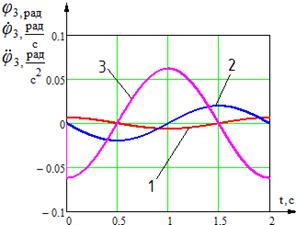
Рис. 3. Временные диаграммы изменения углов, угловых скоростей и угловых ускорений звеньев механизма: 1 - угол поворота звена; 2 - угловая скорость звена; 3 - угловое ускорение звена; а) временные диаграммы изменения угла, угловой скорости и углового ускорения звена 1; б) временные диаграммы изменения угла и угловой скорости звена 2; в) временная диаграмма изменения углового ускорения ![]() звена 2; г) временные диаграммы изменения угла, угловой скорости и углового ускорения звена 3
звена 2; г) временные диаграммы изменения угла, угловой скорости и углового ускорения звена 3
Исследуем другой режим работы трехзвенного механизма, при котором шарнир ![]() движется поступательно. Законы изменения управляющих моментов, полученных также экспериментально можно проследить на следующих диаграммах.
движется поступательно. Законы изменения управляющих моментов, полученных также экспериментально можно проследить на следующих диаграммах.
а)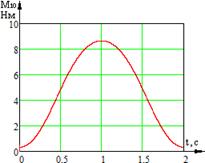 б)
б)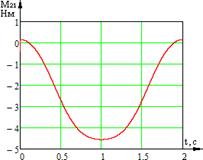 в)
в)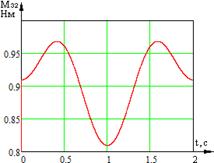
Рис. 4. Временные характеристики изменения моментов звеньев системы:
а) временная характеристика изменения момента ![]() звена 1; б) временная характеристика изменения момента
звена 1; б) временная характеристика изменения момента ![]() звена 2; в) временная характеристика изменения момента
звена 2; в) временная характеристика изменения момента ![]() звена 3
звена 3
Получим диаграммы изменения углов, угловых скоростей, ускорений звеньев трехзвенника для данного режима работы.
а)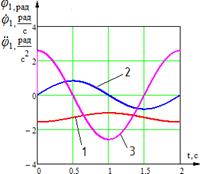 б)
б)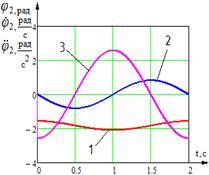 в)
в)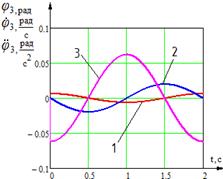
Рис. 5. Временные диаграммы изменения углов, угловых скоростей и угловых ускорений звеньев механизма: 1 - угол поворота звена; 2 - угловая скорость звена; 3 - угловое ускорение звена; а) временные диаграммы изменения угла, угловой скорости и углового ускорения звена 1; б) временные диаграммы изменения угла, угловой скорости и углового ускорения звена 2; в) временные диаграммы изменения угла, угловой скорости и углового ускорения звена 3
Результаты
Разработанная математическая модель аппарата для реабилитации нижних конечностей человека после травм, включающая в себя описание системы управления и конструкции устройства, позволяет выявить закономерности движения трехзвенного механизма и исследовать его динамические свойства. Эта модель может служить основой для создания методов проектирования и выработки оптимального алгоритма управления реабилитационными устройствами.
Работа выполнена при финансовой поддержке РФФИ (грант ФЦП тема 1.196.12П).
Рецензенты:
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ЮЗГУ, г.Курск.
Игнатенко Н.М., д.т.н., профессор, заведующий кафедрой общей и прикладной физики, ЮЗГУ, г.Курск.



