Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Денисова М.Ю. 1

---

1 Казанский федеральный университет

Вырождающиеся эллиптические уравнения представляют собой один из важных разделов современной теории дифференциальных уравнений с частными производными. В статье в n-мерном евклидовом пространстве строятся фундаментальные решения дифференциального уравнения 2m-го порядка с сингулярным оператором Бесселя, действующим по последней переменной. Такое уравнение называем В-полигармоническим уравнением. Для получения фундаментального решения данного уравнения с особенностью в произвольной точке применяется оператор обобщенного сдвига. Такие фундаментальные решения применяются к исследованию краевых задач с условиями типа четности на характеристической части границы. Выводятся первая и вторая формулы Грина. Далее находится интегральное представление найденного решения уравнения, для сведения краевой задачи к системе интегральных уравнений.

Статья в формате PDF

165 KB

полигармоническое уравнение.

дифференциальное уравнение

интегральное представление

1. Денисова М.Ю. Исследование основных краевых задач для некоторых В-полигармонических уравнений методом потенциалов : дис. … канд. физ.-мат. наук. – Казань, 2002. – 99 с.

2. Киприянов И.А., Кононенко В.И. Фундаментальные решения В-эллиптических уравнений // Дифференц. уравнения. – 1967. – Т. 3. – № 1. – С. 114-129.

3. Панич О.И. О потенциалах для полигармонического уравнения четвертого порядка // Матем. сб. – 1960. – Т. 50. – № 3. – С. 335–368.

4. Раджабов Н. Интегральные представления и граничные задачи для некоторых дифференциальных уравнений с сингулярной линией или сингулярными поверхностями. – Душанбе. – 1982. – Ч. 3. – 171 с.

5. Weinstein A. Discontinuous integrals and generalired potential theory // Trans. Am. Math. Soc. – 1948. – № 63. – P. 342-354.

Постановка задачи

Пусть – полупространство  евклидова пространства  точек . Пусть  конечная область в , симметричная относительно плоскости  и ограниченная поверхностью . Обозначим через  часть , расположенную в . Граница области  разбивается  и , расположенными соответственно на плоскости  и в полупространстве . Поверхность  является поверхностью класса , когда [3].

Рассмотрим краевую задачу: найти четное по  решение уравнения

                                                                                                                                                                     (1)

в области ,  раз непрерывно дифференцируемое в  и удовлетворяющее граничным условиям

,

где, если  и , если ,  – внешняя нормаль к границе  в точке , ,  – оператор Бесселя,  – любое положительное число, . Уравнение вида (1) назовем В-полигармоническим уравнением [1].

Фундаментальное решение

Известно [2], что фундаментальные решения уравнения (1) с особенностью в начале координат имеют вид

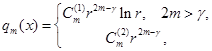
где , .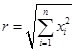

Значения  и  выберем таким образом, чтобы

                                                                              (2)

и

                                                        (3)

для любой четной по  бесконечно дифференцируемой и финитной в  функции .

Можно проверить,  удовлетворяет условиям (2) и (3) при следующих значениях  и :

.

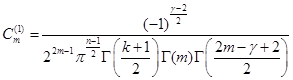
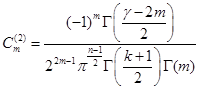С помощью непосредственного подсчета получаем, что

.

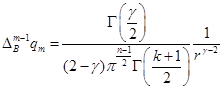Для получения фундаментального решения с особенностью в произвольной точке  применим к функции  оператор обобщенного сдвига [4]:

,

где .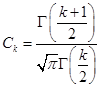

Так как операторы  и  коммутируют, то в силу формальной самосопряженности оператора  из формулы (3) следует, что

.                                                                      

Формулы Грина для функций класса

Пусть  и  четные по  функции класса .

Тогда имеют место тождества

(4)

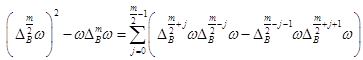 (5)

при четном , и

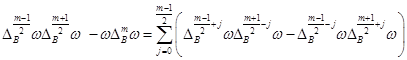(6)

когда  – нечетное число.

Нам понадобятся, для четных по  функций , первая формула Грина

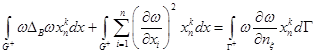
и вторая формула Грина

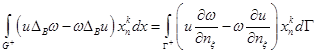.                                   (7)

Интегрируя обе части тождеств (4)–(6) по области  и пользуясь формулой (7), получим обобщенные формулы Грина

,

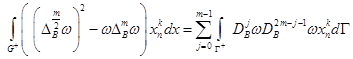для всех четных  и

,                

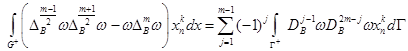когда  – нечетное число, а также имеет место формула

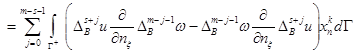
   ,                                                               (8)

где, если  и , если ,  – внешняя нормаль к границе  в точке .

Интегральное представление

Пусть  – внутренняя точка области . Вырежем эту точку шаром  с центром в точке  и радиуса , такого что  (если , то точку  вырежем полушаром ). Поверхность шара обозначим (). Пусть  – решение уравнение (1) в области .

Применяя формулу (8) к функциям  и  в области , с учетом равенства (2), получим

.

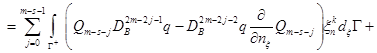
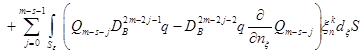Меняя переменную суммирования, и заметив, что  и  в , последнюю формулу можем записать в следующем виде

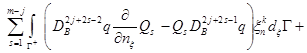
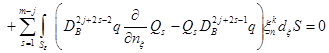.                            (9)

Используя схему, предложенную в работе [5], докажем, что для  и  , имеет такую же особенность в точке , что и фундаментальное решение оператора. Вводя обозначение , получим

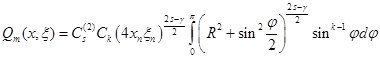.              (10)

Разность между интегралом (10) и интегралом

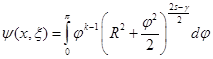
является регулярной функцией в точке , то есть для . В последнем интеграле сделаем замену переменной по формуле . В результате будем иметь

.

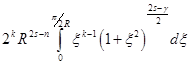Непосредственно вычисляется, что

.

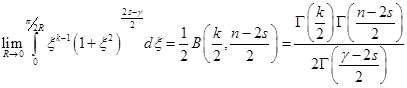Откуда

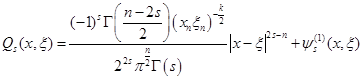.                            (11)

Используя приближенную формулу (11) получаем, что

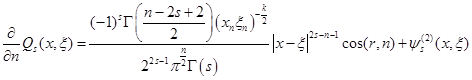(12)

где , и

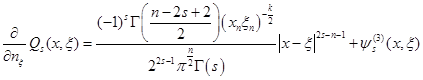(13)

Из приближенных формул (11)–(13) следует, что в формуле (9) первая сумма левой части не зависит от , во второй сумме все слагаемые, кроме слагаемого при  и , сходятся к нулю. Вычислим предел слагаемого при . Его обозначим через . В силу теоремы о среднем значении интеграла, приближенных формул (11)–(13) и с учетом того, что  при , получаем

,

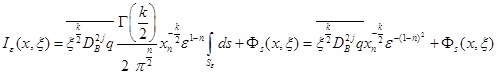то есть .

Таким образом, имеют место следующие интегральные представления для решения уравнения (1):

(14)

Отсюда при  имеем, что

.

Заключение

В работе получено интегральное представление (14) найденного решения уравнения (1), необходимое для сведения краевой задачи к системе интегральных уравнений.

Рецензенты:

Игнатьев Ю.Г., доктор физико-математических наук, профессор, зав. кафедрой высшей математики и математического моделирования, Казанский (Приволжский) федеральный университет, г. Казань.

Сушков С.В., доктор физико-математических наук, профессор, зав. кафедрой теории относительности и гравитации, Казанский (Приволжский) федеральный университет, г. Казань.

Криштоп Виктор Владимирович, доктор физико-математических наук, профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Kwangwoon University, Korea.

Библиографическая ссылка