Наряду с классическим представлением управляемых систем массового обслуживания [3,4], модели СМО могут быть описаны в терминах точечных процессов [2], при которых поведение СМО описывается некоторым случайным процессом, а наличие управляемых воздействий приводит к изменению его траекторий.
В настоящей
работе рассматривается оптимальное управление интенсивностью входящего
пуассоновского потока заявок многоканальной СМО с роутером при эпизодически
наблюдаемой длине очереди на приборах. Рассматриваются две модели СМО: в первой
эпизодический процесс длины очереди строится по наблюдениям в моменты остановки
![]() ; вторая модель строится аналогично
первой, но с введенным процессом телеграфного типа.
; вторая модель строится аналогично
первой, но с введенным процессом телеграфного типа.
Задача нахождения оптимального управления интенсивностью входящего потока двух моделей СМО решается путем нахождения экстремума функционала, зависящего от средней длины очереди на приборах, цены наблюдения и времени моделирования. Решение задачи оптимального управления представлено методами имитационного стохастического моделирования, включающими формальное представление модели, её алгоритмизация, численное нахождение экстремума функционалов, сравнение результатов.
Математическая модель
Рассмотрим
систему массового обслуживания с двумя обслуживающими устройствами с входящим
пуассоновским потоком и моделью роутера (4.2) (детальное описание см. [1]). Введем
процессы ![]() ,
,![]() .
Значения данных процессов соответствуют значениям
.
Значения данных процессов соответствуют значениям ![]() соответственно,
в моменты остановок
соответственно,
в моменты остановок ![]() ,
, ![]() , где
, где ![]() . Обозначим
. Обозначим ![]() как
неубывающее непрерывное справа семейство
как
неубывающее непрерывное справа семейство ![]() -
алгебр
-
алгебр ![]() . Тогда процесс
. Тогда процесс ![]() для
первого обслуживающего устройства принимает вид:
для
первого обслуживающего устройства принимает вид:
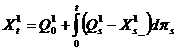 (1)
(1)
Соответственно, для второго обслуживающего устройства процесс записывается как
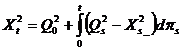 (2)
(2)
Где
![]() .
.
Процессы
![]() ,
,![]() характеризуют
значения очереди в моменты остановок, т.е. фактическое значение длины очереди
на приборе определяется лишь после того, как заявка была распределена в
соответствующую очередь в момент времени
характеризуют
значения очереди в моменты остановок, т.е. фактическое значение длины очереди
на приборе определяется лишь после того, как заявка была распределена в
соответствующую очередь в момент времени ![]() .
Задача заключается в нахождении оптимальной интенсивности наблюдений
.
Задача заключается в нахождении оптимальной интенсивности наблюдений![]() в модели с двумя обслуживающими
устройствами и роутером.
в модели с двумя обслуживающими
устройствами и роутером.
Запишем функционал системы:
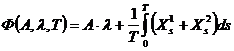 (3)
(3)
Умножив правую часть на
![]() , получим функцию
, получим функцию ![]()
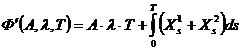 (3’)
(3’)
Где ![]() заданная константа – цена наблюдения,
заданная константа – цена наблюдения, ![]() - время моделирования.
- время моделирования.
Модель (1), (2) с функционалами (3), (3’) можно интерпретировать следующим образом.
Предположим,
что на ![]() -ом обслуживающем устройстве определение
длины очереди происходит только при отправке роутером на соответствующий
-ом обслуживающем устройстве определение
длины очереди происходит только при отправке роутером на соответствующий ![]() прибор. Тогда при
прибор. Тогда при ![]() достигается наилучшая аппроксимация
достигается наилучшая аппроксимация ![]() по наблюдениям
по наблюдениям ![]() ,
,![]() .[7] Однако, при
.[7] Однако, при ![]() второе
слагаемое уравнения (3)
второе
слагаемое уравнения (3) 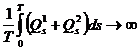 . В то же время, при
. В то же время, при
![]() ,
, 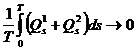 .
.
Таким
образом, оптимизационная задача заключается в нахождении такого параметра ![]() системы, при котором значение
функционала (3) было бы наименьшим.
системы, при котором значение
функционала (3) было бы наименьшим.
![]() (4)
(4)
Рассмотрим
аналогичную модель СМО за исключением того, что в момент остановки (т.е.
прихода заявки на распределительное устройство) у нас есть возможность
определить значение очереди только на одном обслуживающем устройстве. Введем
процесс телеграфного типа ![]() , тогда значение
процессов
, тогда значение
процессов ![]() ,
,![]() будет определено следующим образом:
будет определено следующим образом:
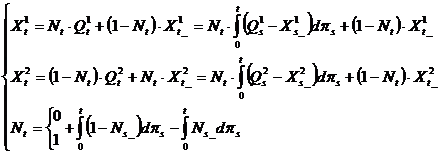 (5)
(5)
Эксперимент, результаты моделирования
Построим
для моделей (2-3), (5) при фиксированном значении ![]() график
функционала (3) в зависимости от
график
функционала (3) в зависимости от ![]() с шагом
с шагом ![]() . Для каждой точки
. Для каждой точки ![]() , где
, где ![]() рассчитаем
значение функционала
рассчитаем
значение функционала ![]() .
.
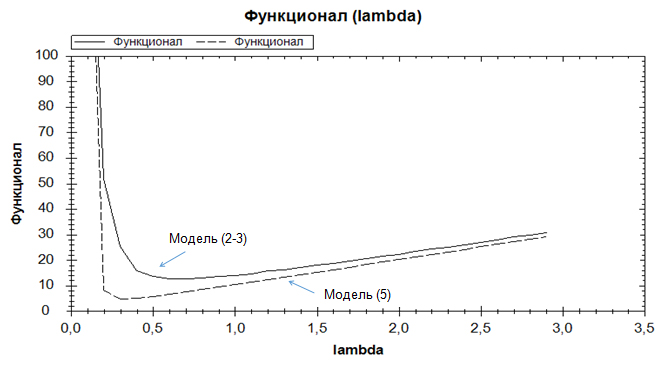
График ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Заключение
Целью настоящей работы являлось
построение задачи и нахождение оптимального управления интенсивностью ![]() входящего потока многоканальной СМО с
роутером при эпизодически наблюдаемой длине очереди на приборах и сравнение
экстремумов двух моделей (2-3) и (5). Численное решение функционала (3) для
моделей (2-3), (5) продемонстрировано на рисунке. Согласно графику, при
заданных параметрах
входящего потока многоканальной СМО с
роутером при эпизодически наблюдаемой длине очереди на приборах и сравнение
экстремумов двух моделей (2-3) и (5). Численное решение функционала (3) для
моделей (2-3), (5) продемонстрировано на рисунке. Согласно графику, при
заданных параметрах ![]() ,
, ![]() для
модели (5)
для
модели (5)![]() , для модели (2-3)
, для модели (2-3) ![]() , при которых значение
, при которых значение ![]() ,
,![]() соответственно.
Модель (5) эффективнее модели (2-3), т.е. при
соответственно.
Модель (5) эффективнее модели (2-3), т.е. при ![]() выполнено
выполнено
![]() . Таким образом, представленная
имитационная модель позволяет находить оптимальную интенсивность наблюдений
. Таким образом, представленная
имитационная модель позволяет находить оптимальную интенсивность наблюдений ![]() в задаче распределения заявок роутером в
системе из двух обслуживающих подсистем.
в задаче распределения заявок роутером в
системе из двух обслуживающих подсистем.
Рецензенты:
Мищенко С.П., д.ф.-м.н., профессор ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск;
Андреев А.С., д.ф.-м.н., профессор ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.
Библиографическая ссылка
Бутов А.А., Галимов Л.А. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ИНТЕНСИВНОСТЬЮ ВХОДЯЩЕГО ПОТОКА МНОГОКАНАЛЬНОЙ СМО С РОУТЕРОМ ПРИ ЭПИЗОДИЧЕСКИ НАБЛЮДАЕМОЙ ДЛИНЕ ОЧЕРЕДИ НА ПРИБОРАХ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=20360 (дата обращения: 21.01.2026).



