В последнее десятилетие огромный интерес теоретических исследований в области гравитации был связан с ролью конформных симметрий, которые возникают на многообразиях, являющихся асимптотически многообразиями с геометрией анти-де Ситтера [1–3]. Классические конформные симметрии фонового многообразия фактически определяют тип дуальной квантовой теории поля, возникающей на границе пространства. Роль конформных симметрий также оказывается важна для подсчета состояний некоторого типа 3-мерных черных дыр [4, 5], и, возможно, имеет ключевое значение для объяснения энтропии физических черных дыр [6].
Цель настоящей работы – обратить внимание на роль конформной симметрии при подсчете энтропии квантового перепутывания квантовых возбуждений на горизонте черной дыры. Для простоты мы рассмотрим случай сферически-симметричных статических черных дыр (решения Шварцшильда или Рейснера-Нордстрема). За счет сферической симметрии любую полевую теорию на данных многообразиях можно редуцировать (в духе Калузы-Кляйна) к "башне" двумерных теорий поля. Поля в каждой такой двумерной теории распространяются только в радиальном направлении. Вблизи горизонта поля являются эффективно безмассовыми, и поэтому обладают двумерной конформной инвариантностью. Отметим, что на значение конформных симметрий при подсчете энтропии перепутывания впервые было обращено внимание в работе [8].
Для того, чтобы продемонстрировать безмассовый характер полевых возбуждений вблизи горизонта, рассмотрим двумерную часть статической метрики
![]() , (1)
, (1)
где координаты ![]() и
и ![]() соответствуют положениям горизонта и границы пространства. На горизонте
соответствуют положениям горизонта и границы пространства. На горизонте ![]() . Для неэкстремальной черной дыры производная
. Для неэкстремальной черной дыры производная ![]() не обращается в ноль, и можно определить константу поверхностной гравитации
не обращается в ноль, и можно определить константу поверхностной гравитации ![]() . Рассмотрим далее в качестве примера скалярное поле
. Рассмотрим далее в качестве примера скалярное поле ![]() на пространстве-времени с метрикой (1). Уравнение для поля имеет следующий вид:
на пространстве-времени с метрикой (1). Уравнение для поля имеет следующий вид:
![]() . (2)
. (2)
Это уравнение сводится к релятивистскому аналогу уравнения Шрёдингера для волновых функций одночастичных полевых возбуждений ![]() с частотой
с частотой ![]() . Производя в уравнении (2) подстановку
. Производя в уравнении (2) подстановку ![]() , приходим к следующей задаче:
, приходим к следующей задаче:
![]() , (3)
, (3)
![]() , (4)
, (4)
где координаты ![]() и
и ![]() связаны соотношением
связаны соотношением ![]() . Как следует из (4), всеми массовыми слагаемыми можно пренебречь из-за наличия множителя
. Как следует из (4), всеми массовыми слагаемыми можно пренебречь из-за наличия множителя ![]() . Поэтому одно-частичный оператор энергии
. Поэтому одно-частичный оператор энергии ![]() есть просто
есть просто ![]() . Аналогичное свойство справедливо для других полей (электромагнитного поля и поля Дирака), см. [9]. Фактически
. Аналогичное свойство справедливо для других полей (электромагнитного поля и поля Дирака), см. [9]. Фактически ![]() вблизи горизонта оказывается гамильтонианом одночастичных возбуждений на ультрастатическом пространстве с метрикой
вблизи горизонта оказывается гамильтонианом одночастичных возбуждений на ультрастатическом пространстве с метрикой
![]() , (5)
, (5)
которая связана с исходной метрикой (1) конформным преобразованием. В (5) положение горизонта отображается на бесконечность, поэтому мы имеем дело с полями, распространяющимися на неограниченном пространстве. Тепловая энтропия таких полей имеет инфракрасную расходимость. Делая размер системы конечным и равным ![]() , можно легко найти свободную энергию
, можно легко найти свободную энергию ![]() , энергию
, энергию ![]() и энтропию
и энтропию ![]() квантов при некоторой температуре
квантов при некоторой температуре ![]()
![]() . (6)
. (6)
Конечный размер ![]() эквивалентен введению обрезания вблизи горизонта на некотором собственном расстоянии
эквивалентен введению обрезания вблизи горизонта на некотором собственном расстоянии ![]() . Причина, по которой от обсуждения энтропии перепутывания мы перешли к обсуждению тепловой энтропии, проста. Энтропия перепутывания связана с потерей информации о квантах, распространяющихся внутри горизонта. Важно, что редуцированная матрица плотности, возникающая при интегрировании по состояниям внутри черной дыры имеет тепловой характер с температурой Хокинга. Поэтому расчет энтропии перепутывания совпадает с вычислением соответствующей тепловой энтропии. Для того, чтобы найти соотношение между параметрами
. Причина, по которой от обсуждения энтропии перепутывания мы перешли к обсуждению тепловой энтропии, проста. Энтропия перепутывания связана с потерей информации о квантах, распространяющихся внутри горизонта. Важно, что редуцированная матрица плотности, возникающая при интегрировании по состояниям внутри черной дыры имеет тепловой характер с температурой Хокинга. Поэтому расчет энтропии перепутывания совпадает с вычислением соответствующей тепловой энтропии. Для того, чтобы найти соотношение между параметрами ![]() и
и ![]() , метрику (1) нужно представить в другой форме:
, метрику (1) нужно представить в другой форме:
![]() . (7)
. (7)
При малых ![]()
![]() , (8)
, (8)
где ![]() – значение конформного фактора на горизонте, а
– значение конформного фактора на горизонте, а ![]() граничное значение
граничное значение ![]() . Энтропия перепутывания, отвечающая вакуумному состоянию Хартла-Хокинга вычисляется при температуре Хокинга
. Энтропия перепутывания, отвечающая вакуумному состоянию Хартла-Хокинга вычисляется при температуре Хокинга ![]() . Для безмассовых полей величина
. Для безмассовых полей величина ![]() в (6) дает точный (в лидирующем приближении) результат для энтропии.
в (6) дает точный (в лидирующем приближении) результат для энтропии.
Покажем теперь, как получить тот же результат используя конформную симметрию. Будем считать, что имеется ![]() безмассовых скалярных полей, тогда в лидирующем приближении
безмассовых скалярных полей, тогда в лидирующем приближении
![]() . (9)
. (9)
Соответствующая конформная теория поля вблизи горизонта характеризуется центральным зарядом ![]() , см. [7]. Центральный заряд определяет коммутационные соотношения алгебры Вирасоро конформной группы. Связь между гамильтонианом системы и генераторами алгебры Вирасоро можно установить, представляя метрику (5) в следующем виде:
, см. [7]. Центральный заряд определяет коммутационные соотношения алгебры Вирасоро конформной группы. Связь между гамильтонианом системы и генераторами алгебры Вирасоро можно установить, представляя метрику (5) в следующем виде:
![]() , (10)
, (10)
![]() . (11)
. (11)
Следовательно,
![]() . (12)
. (12)
Отметим, что в (10) координата ![]() пробегает значения от 0 до
пробегает значения от 0 до ![]() . Этот отвечает теории на интервале, где точки
. Этот отвечает теории на интервале, где точки ![]() и
и ![]() являются независимыми. Для того, чтобы провести вычисления, удобно перейти к теории, где
являются независимыми. Для того, чтобы провести вычисления, удобно перейти к теории, где ![]() является периодической координатой. Это можно сделать, рассматривая две идентичные независимые конформные теории на интервале длиной
является периодической координатой. Это можно сделать, рассматривая две идентичные независимые конформные теории на интервале длиной ![]() , "склеивая" концы интервалов и образуя окружность, так что из двух теорий возникает одна (с областью изменения координаты
, "склеивая" концы интервалов и образуя окружность, так что из двух теорий возникает одна (с областью изменения координаты ![]() от 0 до
от 0 до ![]() ).
).
Теперь имеется две копии алгебры Вирасоро со стандартно определенными элементами ![]() и
и ![]() в качестве генераторов координатных преобразований,
в качестве генераторов координатных преобразований, ![]() и
и ![]() , соответственно. Согласно соотношению (12) гамильтониан системы
, соответственно. Согласно соотношению (12) гамильтониан системы ![]() , который является генератором сдвигов по времени
, который является генератором сдвигов по времени ![]() , представляется в виде:
, представляется в виде:
![]() . (13)
. (13)
Схожим образом, сдвиги системы вдоль координаты ![]() генерируются оператором импульса
генерируются оператором импульса
![]() . (14)
. (14)
Поскольку система находится в покое, среднее значение импульса равно нулю. С другой стороны, среднее значение ![]() совпадает с энергией
совпадает с энергией ![]() , см. (9). Эти условия фиксируют средние значения
, см. (9). Эти условия фиксируют средние значения ![]() и
и ![]() операторов
операторов ![]() и
и ![]() , соответственно. В данном квантовом состоянии
, соответственно. В данном квантовом состоянии
![]() . (15)
. (15)
В пределе, когда ![]() велико (
велико (![]() мало), получаем, что
мало), получаем, что ![]() . В этом случае можно использовать так называемую формулу Карди, чтобы вычислить вырождение
. В этом случае можно использовать так называемую формулу Карди, чтобы вычислить вырождение ![]() и
и ![]() . В рассматриваемом приближении полное вырождение
. В рассматриваемом приближении полное вырождение ![]() есть
есть
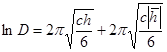 (16)
(16)
и, учитывая, что в нашем случае ![]() , находим
, находим
![]() . (17)
. (17)
Теперь необходимо учесть, что ![]() является числом состояний системы с удвоенным гильбертовым пространством, которое получилось в результате периодизации координаты z. Подлинное число степеней свободы, которое нас интересует равно
является числом состояний системы с удвоенным гильбертовым пространством, которое получилось в результате периодизации координаты z. Подлинное число степеней свободы, которое нас интересует равно ![]() . Для энтропии это дает величину
. Для энтропии это дает величину
![]() , (18)
, (18)
которая в точности совпадает с требуемым значением (9). Чтобы получить энтропию перепутывания в состоянии Хартла-Хокинга, в (18) необходимо положить![]() .
.
Таким образом, на примере упрощенной модели мы показали, что конформная симметрия вблизи горизонта играет важную роль в подсчете степеней свободы черной дыры (если микроскопическое происхождение энтропии Бекенштейна-Хокинга действительно связано с потерей информации внутри горизонта). Дальнейшее исследование проблемы энтропии черной дыры на основе данной симметрии требует отождествления самих степеней свободы и более точного описания их свойств.
Рецензенты:
Исаев А.П., д.ф.-м.н., профессор, заместитель директора Лаборатории теоретической физики им. Н.Н. Боголюбова Объединенного института ядерных исследований, г.Дубна.
Казаков Д.И., д.ф.-м.н, главный научный сотрудник Лаборатории теоретической физики им. Н.Н. Боголюбова Объединенного института ядерных исследований, г. Дубна.
Библиографическая ссылка
Фурсаев Д.В. ОБ ЭНТРОПИИ КВАНТОВОГО ПЕРЕПУТЫВАНИЯ У ГОРИЗОНТА ЧЕРНОЙ ДЫРЫ И КОНФОРМНОЙ СИММЕТРИИ // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12356 (дата обращения: 05.07.2025).



