Краевые задачи для дифференциальных уравнений дробного порядка возникают при описании физических процессов стохастического переноса. Для описания движения примеси в потоке однородной жидкости используется также уравнение дробного порядка [2]. Численным методам решения уравнений с дробными производными посвящена, например, работа [3].
В одномерном случае задачи, когда на границе области помещена
сосредоточенная теплоемкость некоторой величины, рассмотрены в [4]. В работе [10]
построена локально-одномерная схема для многомерного уравнения теплопроводности
с сосредоточенной теплоёмкостью. Здесь рассматривается случай многомерной
задачи для уравнения диффузии дробного порядка, когда на границах области по
каждому направлению ![]() помещена
сосредоточенная теплоёмкость величины
помещена
сосредоточенная теплоёмкость величины ![]() .
Локально-одномерные схемы для решения многомерных задач математической физики
впервые введены в рассмотрение Самарским А.А. [7].
.
Локально-одномерные схемы для решения многомерных задач математической физики
впервые введены в рассмотрение Самарским А.А. [7].
1. ПОСТАНОВКА ЗАДАЧИ
В цилиндре![]() ,
основанием которого является
,
основанием которого является ![]() –мерныйпрямоугольный
параллелепипед
–мерныйпрямоугольный
параллелепипед ![]() с
границей Г, рассматривается задача:
с
границей Г, рассматривается задача:
![]() (1)
(1)
![]() ,
,
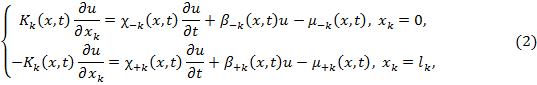
![]()
Коэффициенты
удовлетворяют условиям:![]() ;
;![]() ,
, ![]()
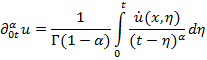
естьрегуляризованная
дробная производная Римана-Лиувилля порядка ![]() ,
,
![]() .
.
2. ЛОКАЛЬНО-ОДНОМЕРНАЯ СХЕМА
В замкнутой
области ![]() строится
сетка
строится
сетка ![]() ,
,
![]() –пространственная
сетка, равномерная по каждому направлению
–пространственная
сетка, равномерная по каждому направлению ![]() ,
,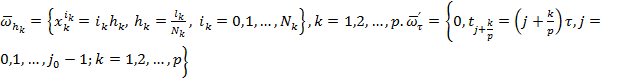 – равномерная сетка, содержащая вместе
с узлами
– равномерная сетка, содержащая вместе
с узлами ![]() так
называемые "фиктивные" узлы
так
называемые "фиктивные" узлы![]() –
множество узлов сетки
–
множество узлов сетки ![]() ,
для которых
,
для которых ![]() .Следуя
[8], многомерному уравнению (1) поставим в соответствие цепочку
"одномерных" уравнений. Для этого уравнение (1) перепишем в виде:
.Следуя
[8], многомерному уравнению (1) поставим в соответствие цепочку
"одномерных" уравнений. Для этого уравнение (1) перепишем в виде:
![]()
или
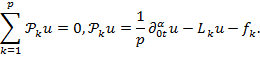
Здесь![]() –
произвольные функции, обладающие той же гладкостью, что и
–
произвольные функции, обладающие той же гладкостью, что и ![]() и
удовлетворяющие условию
и
удовлетворяющие условию![]() На
каждом полуинтервале
На
каждом полуинтервале![]() будем
последовательно решать задачи:
будем
последовательно решать задачи:
![]() (4)
(4)
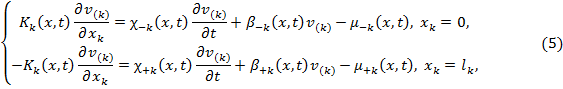
![]()
полагая при этом
![]() (7)
(7)
![]()
Каждое уравнение (4) номера ![]() будем
аппроксимировать на полуинтервале
будем
аппроксимировать на полуинтервале ![]() двухслойным
разностным уравнением. В результате получим цепочку
двухслойным
разностным уравнением. В результате получим цепочку ![]() одномерных
разностных уравнений, которую вместе с граничными и начальными условиями
назовем, следуя [8], локально-одномерной схемой.Итак, цепочка
одномерных
разностных уравнений, которую вместе с граничными и начальными условиями
назовем, следуя [8], локально-одномерной схемой.Итак, цепочка ![]() одномерных
разностных уравнений, соответствующих (4), имеет вид:
одномерных
разностных уравнений, соответствующих (4), имеет вид:
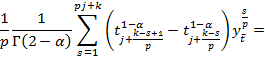
![]() (8)
(8)
где ![]() –
произвольный параметр,
–
произвольный параметр, ![]() –
разностный оператор, соответствующий
–
разностный оператор, соответствующий ![]() ,
,
![]() –
дискретный аналог дробной производной
–
дискретный аналог дробной производной ![]() порядка точности
порядка точности ![]() [4],
[4],
![]()
Будем
рассматривать случай чисто неявной схемы ![]() Задачу
(4)-(6) заменим локально-одномерной разностной схемой:
Задачу
(4)-(6) заменим локально-одномерной разностной схемой:
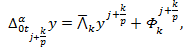 (9)
(9)
![]() (10)
(10)
где
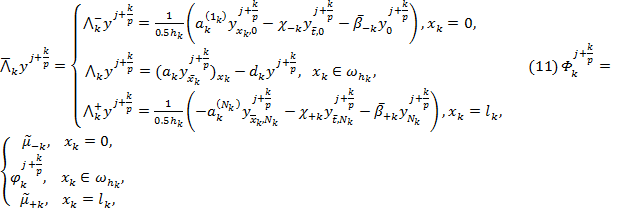 (12)
(12)
![]()
![]()
![]() .
.
3. ПОГРЕШНОСТЬ ЛОКАЛЬНО-ОДНОМЕРНОЙ СХЕМЫ
Сделаем
обозначение ![]() .
Подставляя
.
Подставляя ![]() в (9)-(12) получим задачу для погрешности
в (9)-(12) получим задачу для погрешности ![]() .
Для разностного уравнения получим
.
Для разностного уравнения получим
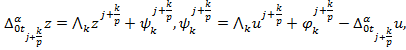 (13)
(13)
где
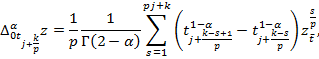
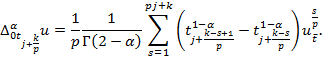
Введем
обозначение ![]() и, замечая, что
и, замечая, что ![]() если
выполнено условие
если
выполнено условие ![]() представим
представим
![]() в
виде суммы
в
виде суммы ![]() где
где
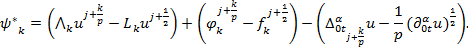
Ясно, что ![]()
Граничное
условие (11) при ![]() перепишем
так
перепишем
так
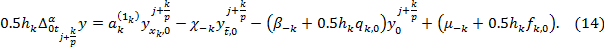
В
(14) подставим ![]() и будем иметь:
и будем иметь:
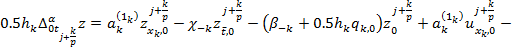
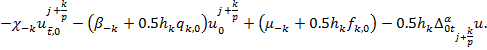
Здесь
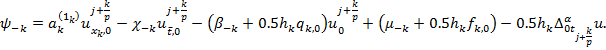
К правой части последнего добавим и отнимем
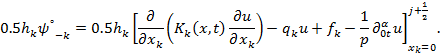
Тогда будем иметь:
![]()
![]()
где
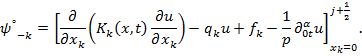
Аналогично
запишется и для граничного условия при ![]() .
Таким образом, имеем
.
Таким образом, имеем
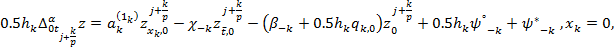
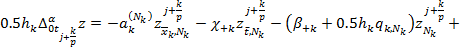
![]()
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() Таким
образом, локально-одномерная схема (9)-(12) обладает суммарной аппроксимацией
Таким
образом, локально-одномерная схема (9)-(12) обладает суммарной аппроксимацией ![]()
4. УСТОЙЧИВОСТЬ ЛОКАЛЬНО-ОДНОМЕРНОЙ СХЕМЫ
Исследование устойчивости локально-одномерной схемы (9)-(10) будем проводить с помощью принципа максимума. Для этого разностное уравнение и граничное условия приведем к каноническому виду [6]:
![]()
где ![]() ,
,![]() узлы
сетки,
узлы
сетки, ![]() –
окрестность узла
–
окрестность узла ![]() ,
не содержащая самого узла
,
не содержащая самого узла ![]() .
Коэффициенты
.
Коэффициенты ![]() и
и
![]() должны
удовлетворять условиям
должны
удовлетворять условиям
![]()
Обозначим
через ![]() узел
узел![]() -мерной
сетки
-мерной
сетки ![]() ,
где
,
где ![]() ,
,
![]() ;
через
;
через ![]() –
границу сетки
–
границу сетки ![]() ,
состоящую из узлов
,
состоящую из узлов ![]() при
при
![]() и
узлов
и
узлов ![]() при
при
![]() и
и
![]() для
всех значений
для
всех значений ![]() и
и ![]() .
.
Распишем уравнение (9)
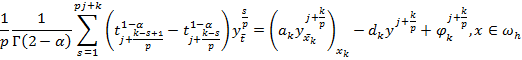
в индексной форме и приведем к каноническому виду (15). Имеем:
![]()
![]()
![]()
![]() .
(17)
.
(17)
Здесь заметим, что
![]()
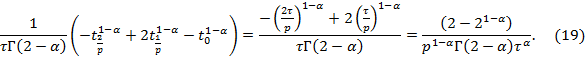
С учетом (18), (19) перепишем уравнение (17):
![]()
![]()
![]()
![]()
где ![]()
Приведем
теперь граничные условия (11) для ![]() и
и![]() к
каноническому виду. Для
к
каноническому виду. Для ![]() с
учетом(18), (19) имеем:
с
учетом(18), (19) имеем:
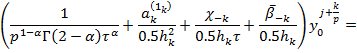
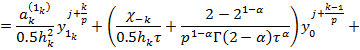
![]()
![]()
где ![]()
Аналогично
для краевого условия при ![]() с
учетом (18), (19) имеем:
с
учетом (18), (19) имеем:
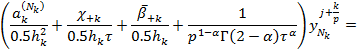
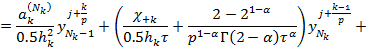
![]()
![]()
где
![]()
Из (20)-(22) находим:
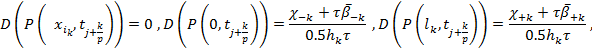
где ![]()
Представим
теперь решение задачи (9)-(12) в виде суммы ![]() ,где
,где
![]() –
решение задачи при
–
решение задачи при ![]() ,
,
![]() ;
;
![]() –
решение задачи при
–
решение задачи при ![]() (
(![]() ).Оценки
для решения
).Оценки
для решения ![]() и
и
![]() будем
получать с помощью принципа максимума для сеточного уравнения каноническоговида
(15) при выполнении на коэффициенты условий (16).Итак, имеем задачи для
будем
получать с помощью принципа максимума для сеточного уравнения каноническоговида
(15) при выполнении на коэффициенты условий (16).Итак, имеем задачи для![]() и
и
![]() соответственно:
соответственно:
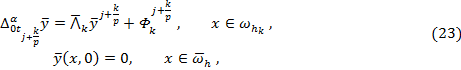
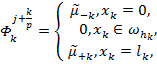 (24)
(24)
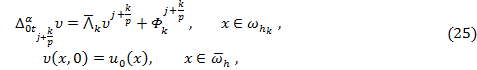
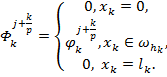 (26)
(26)
где операторы ![]() и
и ![]() имеют вид (11). Уравнение в (23) в канонической форме запишем:
имеют вид (11). Уравнение в (23) в канонической форме запишем:
![]()
![]()
![]()
![]()
Далее
воспользуемся леммой из [4], согласно которой при![]() имеет
место неравенство
имеет
место неравенство
![]() ,
, ![]() . (28)
. (28)
С учетом (28)
выражения в круглых скобках положительны.Имеем, что для коэффициентов ![]() ,
,
![]() и
и
![]() в
уравнении (27) выполнены условия (16) и
в
уравнении (27) выполнены условия (16) и ![]() .
На основании теоремы 3 ([6], с.344) для
.
На основании теоремы 3 ([6], с.344) для ![]() получаем
оценку:
получаем
оценку:
![]()
Для
оценки![]() перепишем
уравнение в (25) в виде:
перепишем
уравнение в (25) в виде:
![]()
![]()
где
![]()
![]() .
.
Проверим выполнение условий теоремы 4 ([6], с.347):
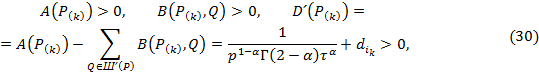
![]() ,
,
![]() .Условия (30) выполняются для всех
.Условия (30) выполняются для всех ![]() ,
,
![]() ,
,
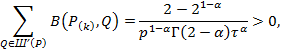
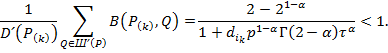
Здесь ![]() –
множество узлов
–
множество узлов ![]() ,
,
![]() –
множество узлов
–
множество узлов ![]() .
.
Итак,
на основании теоремы 4 (см. [6], с.347) для функции ![]() после
суммирования по
после
суммирования по ![]() ,
а затем по
,
а затем по ![]() имеем
оценку:
имеем
оценку:
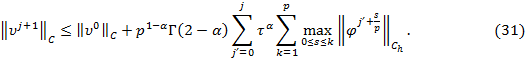
Собирая оценки (29) и (31), получаем окончательную оценку:
![]()
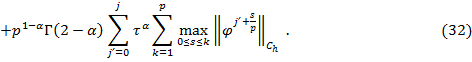
Из априорной оценки (32) следует устойчивость локально-одномерной схемы (9)-(12) по входным данным задачи.
5. РАВНОМЕРНАЯ СХОДИМОСТЬ ЛОКАЛЬНО-ОДНОМЕРНОЙ СХЕМЫ
Чтобы
использовать свойство![]() представим,
по аналогии с [8], решение задачи для погрешности (13) в виде суммы
представим,
по аналогии с [8], решение задачи для погрешности (13) в виде суммы![]() .В
этой сумме функция
.В
этой сумме функция ![]() определяется
условиями:
определяется
условиями:
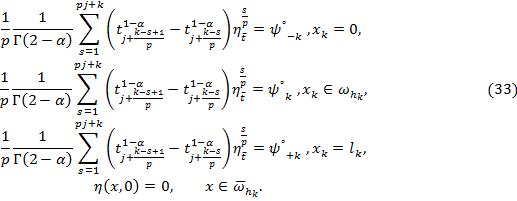
Функция ![]() определяется
условиями:
определяется
условиями:
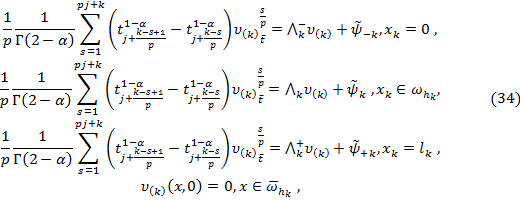
где ![]() ,
,
![]() ,
,![]()
На кубической
сетке ![]() при
условиях
при
условиях ![]() ,
,
![]() справедливо:
справедливо:
![]() ,
, ![]() ,
,![]()
![]() ,
,
где ![]() –
известные постоянные. Если существуют непрерывные в замкнутой области
–
известные постоянные. Если существуют непрерывные в замкнутой области ![]() производные
производные![]() ,
то
,
то ![]() .Для оценки решения задачи (34)
воспользуемся оценкой (32):
.Для оценки решения задачи (34)
воспользуемся оценкой (32):
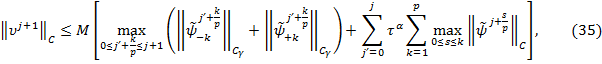
где ![]() независящая
от
независящая
от ![]() и
и
![]() .Из
оценки (35) находим, что
.Из
оценки (35) находим, что
![]()
откуда получаем
![]()
Таким образом, справедлива следующая
Теорема.Пусть задача (1)-(3)
имеет единственное и непрерывное в![]() решение и существуют
непрерывные в
решение и существуют
непрерывные в ![]() производные
производные
![]()
![]() ,
,![]() ,
,
тогда решение разностной схемы (9)-(12) равномерно сходится
к решению дифференциальной задачи (1)-(3) со скоростью ![]() ,
, ![]() .
.
Шхануков-Лафишев М. Х., д.ф.-м.н., профессор,ФГБУН Институт информатики и проблем регионального управления Кабардино-Балкарского научного центра РАН, г. Нальчик;
Ашабоков Б.А.,д.ф.-м.н., профессорВысокогорного Геофизического Института, г. Нальчик.



