Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Глебов А.Л. 1 Миндеева А.А. 1 Петросян В.С. 1 Геворгян А.М. 1

---

1 Национальный исследовательский университет «МИЭТ»

В статье описывается логическое моделирование цифровых КМОП схем при помощи диаграмм троичных решений. Производится оценка затрачиваемой схемой мощности как пример использования такого моделирования. Как вводная информация объясняется сутью представления Булевых функций в виде диаграмм двоичных решений (BDD). Для описания неполно определенных Булевых функций вида f: Tn->T, T={0,U,1} представляются диаграммы троичных решений (TDD) и вводится понятие последовательно-паралельных диаграмм троичных решений (SP-TDD). На основе представления КПОМ схемы в виде SP-BDD описывается алгоритм построения SP-TDD модели цифровых КМОП схем. Логическое моделирование цифровых схем с использованием TDD дает возможность оптимизации цифровой схемы и оценки параметров цифровой схемы с учетом третьего, неопределенного состояния вентилей. В работе производится логическое моделирование цифровой схемы и оценка потребляемой схемой мощности. В случае TDD представления оценка потребляемой мощности имеет интервальное значение, так как в модели существуют узлы с неопределенным значением и, следовательно, с неопределенным переключением. В последующем эти интервальные значения можно уточнить путем наложения дополнительной информации.

Статья в формате PDF

132 KB

оценка потребляемой мощности

диаграммы троичных решений

SP-TDD

диаграммы двоичных решений

моделирование цифровых схем

логическое моделирование

1. Глебов А. Л., Гурарий М. М., Жаров М. М. и др. Актуальные проблемы моделирования в системах автоматизации схемотехнического проектирования. М.: Наука, 2003. 436 с.

2. Bryant R. E. Graph-based algorithms for Boolean function manipulation // IEEE Trans. on Computers, v.C-35, 1986, pp.677-691.

3. Glebov A. L., Blaauw D., Jones L. G. Transistor reordering for low power CMOS gates using SP-BDD representation // Int. Symp. on Low Power Design, Dana Point CA, 1995, pp.161-166.

4. Glebov A. L., Gavrilov S. V., Blaauw D. et. al. Library-Less Synthesis for Static CMOS Circuits // ICCAD-97, pp.461-467.

5. Jennings G. Symbolic Incompletely Specified Functions for Correct Evaluation in the Presence of Indeterminate Input Values // Proc. of 28th Annual Hawaii Int. Conf. on System Sciences, 1995, pp.23-31.

6. Kleene S. C. Introduction to Methamatematics / Amsterdam: North-Holland Publishing Co., 1952. 576 p.

7. Meinel C., Theobald T. Algorithms and Data Structures in VLSI Design. Berlin: Springer-Verlag, 1998. 123 p.

8. Popel D. V. Visualization and Manipulation of Incomplete and Uncertain Dependencies by Decision Diagrams // Journal of Universal Computer Science, v.11, pp.1849-1862.

Введение

Хорошо известно, что BDD (диаграммы двоичных решений) являются удобным и эффективным представлением Булевых функций f: Bn->B, B={0,1} [2],[7]. Это представление позволяет конструировать и программно реализовывать различные алгоритмы для работы с системами Булевых функций. В частности, это алгоритмы логического синтеза, верификации и генерации тестов для цифровых схем. Сюда же можно отнести и алгоритм логического моделирования.

Известна также SP-BDD (последовательно-параллельная диаграмма двоичных решений), которая представляет собой BDD специального вида и является адекватной моделью цифровых КМОП схем [1],[3]. SP-BDD содержит в себе полную информацию не только о Булевой функции, вычисляемой КМОП вентилем, но также и о его детальной электрической схеме на транзисторном уровне. Кроме логического моделирования, SP-BDD может быть использована для оперативной и достаточно точной оценки задержек и потребляемой мощности цифровых КМОП схем, а также для их ресинтеза (структурной оптимизации) [4] и во многих других приложениях. На практике часто приходится иметь дело с неполно определенными Булевыми функциями вида f: Tn->T, T={0,U,1}. Дополнительное состояние U может интерпретироваться различными способами. Чаще всего оно интерпретируется в рамках Клиниевой сильной трехзначной логики (Kleenean strong ternary logic) [6], в которой U – это состояние «не определено» (undefined = don't care). Т. е. это в действительности либо 0, либо 1, но мы не знаем что именно (или нам не нужно это знать). Значение U может принимать как каждый из аргументов, так и сама неполно определенная Булева функция. Далее для таких функций будем для краткости использовать термин «Клиниева функция».

По аналогии с BDD, удобным представлением для Клиниевой функции является TDD (диаграмма троичных решений) [5],[8]. В TDD каждая нетерминальная вершина имеет трех потомков, кроме того имеются три терминальные вершины, соответствующие значениям функции 0,U,1. По умолчанию, под TDD обычно понимают ROTDD, т. е. минимизированную упорядоченную TDD. По аналогии с BDD, для заданной Клиниевой функции TDD строится в три этапа:

• выбирается порядок аргументов;
• в соответствии с таблицей истинности функции строится троичное дерево;
• производится редукция (минимизация) троичного дерева, т. е. удаляются вершины, у которых все три потомка совпадают, и удаляются изоморфные подграфы.

Таким образом построенная TDD является каноническим (единственным) представлением Клиниевой функции (для заданного порядка аргументов). Для TDD разработан ряд алгоритмов и пакетов программ, аналогичных таким для BDD. Наиболее очевидным применением TDD является логическое моделирование соответствующих цифровых схем.

Построенная вышеуказанным способом TDD называется полной TDD. Если мы удалим из нее все U-ветви (и все, что определяется только ими), мы получим так называемую сокращенную (abbreviated) TDD [5], [8]. Сокращенная TDD также является каноническим представлением Клиниевой функции. По сокращенной TDD может быть однозначно восстановлена полная TDD. Однако сокращенная TDD занимает значительно меньше места в компьютерной памяти. Поэтому во многих алгоритмах выгоднее использовать сокращенную TDD, а полную TDD восстанавливать только тогда, когда это необходимо (например, при логическом моделировании). Пример полной и сокращенной TDD для функции f(a,b,c)=ab+c показан на рис. 1. (Следует отметить, что для некоторых функций U-терминал может сохраняться в сокращенной TDD.)

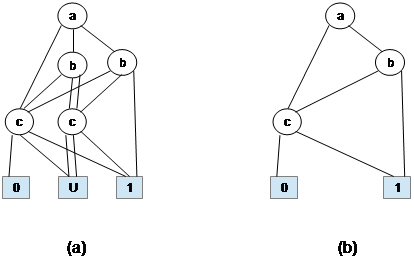
Рис. 1. Полная (a) и сокращенная (b) TDD для функции f(a,b,c)=ab+c

В общем случае ветви TDD, идущие вниз от нетерминальной вершины, должны быть помечены значками ”0”,”U”,”1”, указывающими, какому значению переменной в данной вершине соответствует данная ветвь. В TDD на рис.1(a) подразумевается, что ветви, идущие от каждой вершины, помечены по умолчанию слева направо соответственно символами ”0”,”U”,”1” (на рис. 1(b) — символами ”0”,”1”). Однако такая умолчательная разметка удобна далеко не всегда.

В настоящей работе, по аналогии с SP-BDD, вводится понятие SP-TDD (последовательно-параллельная диаграмма троичных решений). SP-TDD является адекватной моделью цифровых КМОП схем, рассматриваемых в рамках Клиниевой логики (т. е. с возможностью неопределенных значений логических сигналов). Предложен метод логического моделирования цифровых схем, основанный на использовании TDD и позволяющий вычислять интервальную оценку потребляемой мощности. Приведены результаты численных экспериментов, полученные с помощью экспериментальной программы логического моделирования с неопределенностью и показывающие эффективность предлагаемых методов.

SP-TDD модель цифровых КМОП схем

Приведем сначала определение SP-BDD через рекурсивную процедуру ее построения [1] (рис. 2).

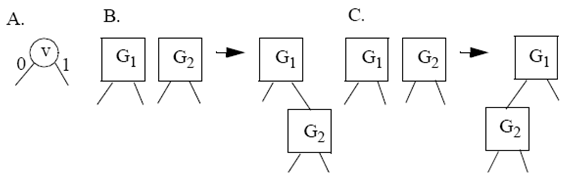
Рис. 2. Рекурсивное построение SP-BDD: A. SP-BDD для одного ключа

B. Формирование SP-BDD для последовательного соединения двух ПП-цепей

C. Формирование SP-BDD для параллельного соединения двух ПП-цепей

По аналогии с вышеприведенным определением, дадим рекурсивное определение SP-TDD как модели Клиниевой функции, задаваемой последовательно-параллельной цепью (ПП-цепью) из ключей (с возможностью третьего, неопределенного состояния как каждого ключа, так и всей цепи). Данное определение показано на рис. 3.

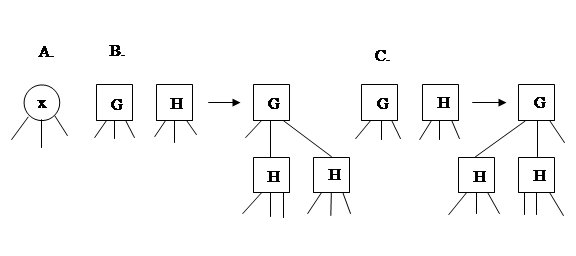
Рис. 3. Рекурсивное построение SP-TDD: A. SP-TDD для одного ключа

B. Формирование SP-TDD для последовательного соединения двух ПП-цепей

C. Формирование SP-TDD для параллельного соединения двух ПП-цепей

При графическом изображении SP-TDD (рис. 3), помимо вышеупомянутой умолчательной разметки ветвей, используется следующее соглашение (естественное для SP-TDD).

Если для некоторой ветви явно не показан потомок, то им является: 0-терминал для ветви идущей вниз-влево; U-терминал для ветви идущей строго вниз; 1-терминал для вершины идущей вниз-вправо.

Отметим два важных факта. Во-первых, как и в случае SP-BDD, SP-TDD может быть построена не только через построение троичного дерева (см. выше), но также и через последовательность присоединений параллельно и последовательно соединенных фрагментов.

Во вторых, из сравнения рис. 2, 3 видно, что сокращенная SP-TDD, полученная из полной удалением U-ветвей, есть не что иное, как соответствующая SP-BDD.

Логическое моделирование на основе TDD и оценка мощности

При логическом моделировании цифровой схемы с использованием BDD мы, разумеется, можем попутно получать оценки различных величин: например, потребляемой мощности. Аналогично, при моделировании на основе TDD (т. е. с возможностью третьего, неопределенного значения сигнала) мы также можем оценивать потребляемую мощность. Однако в этом случае мы получаем интервальную оценку мощности; границами интервала являются минимальное и максимальное из возможных значений мощности.

Рассмотрим возможные переключения логического вентиля G при переходе схемы от некоторого входного вектора к следующему. Пусть энергия, потребляемая вентилем при переключении, равна EG. Возможны три варианта для потребляемой энергии E при следующих переключениях выхода вентиля:

E принадлежит [0,0] при 0->0, 1->1

E принадлежит [EG,EG] при 0->1, 1->0

E принадлежит [0,EG] при 0->U, U->0, 1->U, U->1, U->U

В соответствии с данным подходом, оценка мощности, основанная на логическом моделировании на основе TDD, состоит из следующих шагов:

a) Для моделируемой схемы, заменить каждый вентиль его TDD-представлением;

b) Инициализировать состояние схемы в соответствии с нулевым входным вектором;

c) Инициализировать полную энергию интервалом [0,0], максимальную энергию – нулем;

d) Для каждого последующего входного вектора повторить пп. e-k;

e) Инициализировать тактовую энергию интервалом [0,0];

f) Для каждого вентиля, в топологическом порядке (от входов к выходам), повторить пп. g-i;

g) Определить новое состояние выхода вентиля, найдя в его TDD путь для нового состояния его входов;

h) Определить интервальную оценку энергии, потребленной вентилем на данном такте;

i) Добавить интервальную оценку энергии, потребленной вентилем, к тактовой энергии;

j) Добавить тактовую энергию к полной энергии;

k) Обновить максимальную энергию в соответствии с тактовой энергией;

l) По полной энергии и времени моделирования вычислить интервальную оценку мощности.

Результаты эксперимента

В результате логического моделирования цифровой КМОП схемы с использованием TDD и последующем анализе потребляемой схемой мощности были получены интервальные значения мощностей при переключениях для разнообразных схем. Для каждой схемы были проведены два эксперимента с разным количеством неопределенных входов во входном векторе.

В Таблице 1 приведены результаты эксперимента для 6-и схем. Для каждой схемы выбраны два входных вектора по количеству неопределенных входов (UND в таблице). Название схем и количество транзисторов в схеме указаны в колонках 1 и 2. В колонках 2, 3, 4 указаны, соответственно, количество входов, количество выходов схем и количество неопределенных входов. В колонке 6 указана процентная доля транзисторов в неопределенном состоянии от их общего числа. В колонках 7,8,9, соответственно, минимальная мощность, максимальная мощность и пиковая мощность. Количество циклов – 2000 на все схемы.

Таблица 1

Заключение

Логическое моделирование цифровых схем с использованием TDD дает возможность оптимизации цифровой схемы и оценки параметров цифровой схемы с учетом третьего, неопределенного состояния вентилей. В данном случае была рассмотрена потребляемая схемой мощность при переключениях и были получены интервальные значения потребляемой мощности. В последующем эти значения можно уточнить путем наложения импликаций.

Рецензенты:

Амербаев В.М., д.т.н., профессор, главный научный сотрудник ИППМ РАН, г. Зеленоград.

Гаврилов С.В., д.т.н., профессор НИУ МИЭТ, г. Зеленоград.

Библиографическая ссылка