Введение
В современной гражданской авиации широко применяются двухконтурные турбореактивные двигатели. Для создания надежного двигателя необходимо проведение исследований прочности его деталей и узлов. Важной проблемой является исследование колебаний и вибрационной прочности рабочих колес [7]. Для проведения экспериментов по исследованию вибронапряжений требуется предварительный численный анализ вибрационных характеристик конструкций. По результатам такого анализа могут быть определены дальнейшие методы экспериментального исследования.
В работе производится оценка динамических характеристик трехмерной модели методом конечных элементов, что позволяет учесть влияние геометрических форм и нагрузок. Тема работы представляет несомненный интерес для отдела прочностного проектирования роторов и лопаток ОАО «Авиадвигатель» и других промышленных предприятий аналогичного профиля. Исследование необходимо для численного моделирования экспериментальных работ, связанных с турбиной низкого давления. Проведение таких расчетов и анализ результатов позволяет на стадии планирования эксперимента оценить вероятность возникновения резонансных режимов, тип и количество используемых тензодатчиков, места их расположения. Проведение численного моделирования эксперимента позволяет существенно снизить стоимость самого эксперимента.
Цель работы: осуществить численное исследование динамических характеристик рабочего колеса. Для достижения поставленной цели требуется решить следующие задачи: провести численный расчет собственных частот и форм колебаний рабочего колеса с учетом предварительного напряженного состояния, построить дисперсионные и резонансные диаграммы, определить резонансные режимы рабочего колеса, выявить дисковые формы колебаний, определить распределение динамических напряжений при дисковых формах колебаний.
В работе рассматривается одно рабочее колесо, являющееся шестой ступенью турбины низкого давления (ТНД) перспективного авиационного двигателя. В качестве модели рабочего колеса с рабочей лопаткой рассматривается сектор, полученный сечением колеса двумя поверхностями, угол между которыми составляет 360̊/102. В работе рассматривается сектор с одной лопаткой (общее количество – 102 шт.), так как рабочее колесо является объектом с поворотной симметрией с порядком симметрии (S) равным количеству лопаток.
Множество собственных частот и форм колебаний распадается на группы. Каждой группе соответствует определенное количество узловых диаметров (m). В работе набор частот находится для каждого узлового диаметра в отдельности. В общем случае число групп равно порядку симметрии, но из-за особенностей поворотно-симметричных систем появляются двукратные собственные частоты, поэтому количество узловых диаметров для такой системы равно S/2 [2]. В нашем случае количество узловых диаметров равно 51.
Для получения предварительного напряженного состояния решается контактная задача об определении НДС рабочего колеса. Взаимодействие диска и лопатки моделируется заданием контактных элементов на контактных поверхностях замкового соединения. Условия контакта используются и на бандажной полке лопатки для рассмотрения взаимодействия рабочих лопаток в колесе. Задача решается в трехмерной постановке в предположении упругого поведения материала деталей.
Математическая постановка задачи включает в себя [4]:
Уравнения равновесия:
![]() ,
,
где ![]() – плотность материала.
– плотность материала.
Физические соотношения:
![]() ,
,
где ![]() ,
, ![]() – упругие постоянные Ламе, характеризующие свойства изотропного материала,
– упругие постоянные Ламе, характеризующие свойства изотропного материала, ![]() – объемная деформация,
– объемная деформация, ![]() – символ Кронекера,
– символ Кронекера, ![]() – изотермический модуль объемного сжатия,
– изотермический модуль объемного сжатия, ![]() – коэффициент линейного температурного расширения,
– коэффициент линейного температурного расширения, ![]() – изменение температуры.
– изменение температуры.
Геометрические соотношения:
![]() .
.
Граничные условия:
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() – нормаль к поверхности тела в рассматриваемой точке,
– нормаль к поверхности тела в рассматриваемой точке, ![]() – известные поверхностные внешние усилия в рассматриваемой точке,
– известные поверхностные внешние усилия в рассматриваемой точке, ![]() – известные значения перемещений,
– известные значения перемещений, ![]() – поверхность тела, на которой заданы граничные условия,
– поверхность тела, на которой заданы граничные условия, ![]() – часть поверхности тела, на которой заданы статические граничные условия,
– часть поверхности тела, на которой заданы статические граничные условия, ![]() – часть поверхности тела, на которой заданы кинематические граничные условия.
– часть поверхности тела, на которой заданы кинематические граничные условия.
В рассматриваемой модели рабочего колеса запрещены осевые перемещения на фланцах диска, а также в одной из точек нижней цилиндрической поверхности ступицы диска для исключения перемещения колеса как единого целого.
Уравнение свободных колебаний:
![]() .
.
Контактное взаимодействие задается следующим образом:
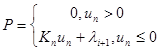 ;
;
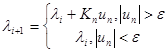 ,
,
где ![]() – контактное давление,
– контактное давление, ![]() – нормальная жесткость контакта,
– нормальная жесткость контакта, ![]() – расстояние между контактными поверхностями,
– расстояние между контактными поверхностями, ![]() – множитель Лагранжа на
– множитель Лагранжа на ![]() -ой итерации,
-ой итерации, ![]() – допуск совместности.
– допуск совместности.
Расширенный метод Лагранжиана находит множители Лагранжа для каждого элемента, производя серию итераций по расчету штрафов.
Поставленная задача решается методом конечных элементов [5]. Расчет проводится в пакете конечно-элементного анализа ANSYS.
Общий вид модели рабочего колеса шестой ступени ТНД показан на рис. 1.

В качестве расчетного режима рассматривается взлет, так как данный режим работы является более нагруженным. При расчете НДС рабочего колеса учитываются следующие силовые воздействия:
- давление от газовых сил на поверхности корыта и спинки лопатки;
- угловая скорость вращения ротора ТНД для расчетного режима;
- температура лопатки и диска, соответствующая расчетному режиму.
Для получения результатов для всего рабочего колеса при решении одного сектора в ANSYS используется анализ с циклической симметрией. Соответствующее условие задается на поверхностях, вырезающих сектор рабочего колеса. Количество лопаток в колесе задается равным 102.
Решается задача об определении собственных частот и соответствующих им форм колебаний конструкции с учетом предварительного напряженного состояния, вызванного действующими на конструкцию во взлетном режиме силовыми факторами, для чего в пакете ANSYS выполняется предварительный статический расчет НДС. Модальный анализ в пакете ANSYS выполняется для всех узловых диаметров в диапазоне частот от 0 до 9500. Диапазон с большими значениями не рассматривался, в связи с отсутствием пересечений с представляющими интерес гармониками возбуждения. Для дальнейшего построения резонансных диаграмм модальный анализ также проводится и без учета предварительного напряженного состояния.
Анализ результатов
По результатам расчетов строится дисперсионная диаграмма (рис. 2), на которой крестами отмечены все найденные собственные частоты. По точкам строятся линии, соединяющие частоты с одним порядковым номером по всем узловым диаметрам. Обработка данных, полученных в процессе выполнения численных экспериментов и представленных на рис. 2 проводится в пакете MATLAB. Данные передаются из ANSYS в MATLAB в виде текстового файла.
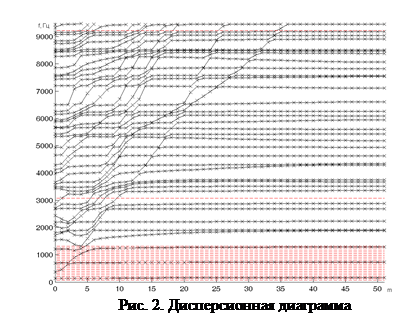
В результате анализа собственных форм и диаграммы выявлено, что при лопаточных формах колебаний собственная частота почти не изменяется с увеличением количества узловых диаметров. При дисковых формах колебаний частота значительно возрастает, на дисперсионной диаграмме можно видеть скачки. По этим точкам можно увидеть, как изменяются дисковые формы колебаний при увеличении количества узловых диаметров. Красными пунктирными линиями отмечены рассматриваемые далее гармоники.
Для построения по полученным результатам резонансных диаграмм и определения резонансных режимов создана еще одна программа в пакете MATLAB. Программа позволяет в автоматическом режиме строить графики; находить пересечения гармоник возбуждения с функциями, описывающими изменение собственных частот в зависимости от частоты вращения; делать необходимые подписи на графиках; сохранять полученные рисунки в формате .png, а также записывать таблицы с найденными резонансными режимами в файл .xls. Программа работает, используя текстовые файлы с полученными в ANSYS результатами и данными, вводимыми пользователем перед запуском, в зависимости от того, какие диапазоны частот и гармоники интересны для рассмотрения.
Резонансные диаграммы строятся по двум точкам, при «нулевой» нагрузке и при максимальной частоте вращения в режиме взлета. Гармоники возбуждения строятся по формуле
![]() ,
,
где ![]() – целые числа, указывающие на номер гармоники возбуждения,
– целые числа, указывающие на номер гармоники возбуждения, ![]() – частота вращения рабочего колеса [6].
– частота вращения рабочего колеса [6].
При анализе резонансных режимов рассматриваются следующие диапазоны изменения частоты вращения рабочего колеса: земной малый газ, полетный малый газ и режим взлета. При этом учитывается возбуждение по низшим гармоникам с первой по двадцатую и по высоким гармоникам ![]() равным, соответственно, количеству блоков и лопаток соплового аппарата 6 ступени. На рис. 3 показан пример резонансной диаграммы для случая с 8 узловыми диаметрами. Остальные диаграммы аналогичны, различаются лишь значения.
равным, соответственно, количеству блоков и лопаток соплового аппарата 6 ступени. На рис. 3 показан пример резонансной диаграммы для случая с 8 узловыми диаметрами. Остальные диаграммы аналогичны, различаются лишь значения.
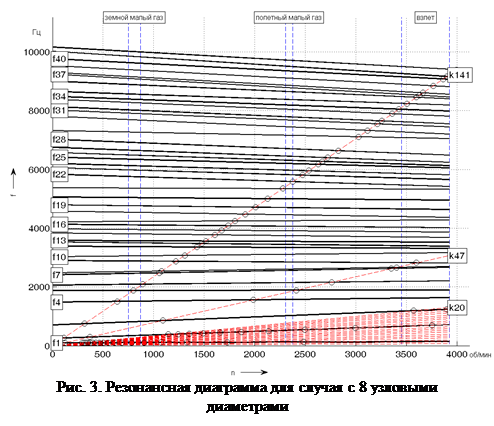
На резонансных диаграммах кружками отмечены пересечения лучей гармоник возбуждения с собственными частотами. Если номер гармоники не совпадает с количеством узловых диаметров, то резонанса в таких точках нет [3]. Это объясняется взаимной ортогональностью форм колебаний и окружного распределения возбуждающих сил, при которой поступление энергии от источника возбуждения на поддержание колебаний системы отсутствует [6]. Для систем с ограниченным порядком симметрии исключение представляют гармоники с номерами:
![]() ,
,
где ![]() – количество волн,
– количество волн, ![]() – порядок симметрии,
– порядок симметрии, ![]() – номер гармоники.
– номер гармоники.
Такие гармоники также могут поддерживать колебания по собственным формам, имеющим ![]() волн. Это условие также учтено в программе, что избавляет от необходимости вручную считать, с какими узловыми диаметрами и по каким гармоникам возбуждения возможен резонанс.
волн. Это условие также учтено в программе, что избавляет от необходимости вручную считать, с какими узловыми диаметрами и по каким гармоникам возбуждения возможен резонанс.
В результате анализа были определены резонансные режимы, указанные в табл. 1: В таблице f – собственные частоты, k – гармоники возбуждения.
Таблица 1. Расчетные резонансные режимы
|
Номер собственной частоты (f) |
Номер гармоники возбуждения (k) |
Узловые диаметры |
Частота вращения, об/мин |
Собственная частота, Гц |
|
1 |
8 |
8 |
779,6736 |
103,9565 |
|
2 |
11 |
11 |
3857,374 |
707,1853 |
|
3 |
20 |
20 |
3757,408 |
1252,469 |
|
4 |
141 |
39 |
804,0695 |
1889,563 |
|
5 |
141 |
39 |
848,4997 |
1993,974 |
|
18 |
141 |
39 |
2361,737 |
5550,083 |
|
28 |
141 |
39 |
3480,233 |
8178,548 |
|
29 |
141 |
39 |
3598,983 |
8457,61 |
|
30 |
141 |
39 |
3630,434 |
8531,52 |
|
31 |
141 |
39 |
3646,35 |
8568,923 |
|
32 |
141 |
39 |
3798,615 |
8926,745 |
|
33 |
141 |
39 |
3854,471 |
9058,007 |
|
34 |
141 |
39 |
3908,506 |
9184,989 |
|
8 |
47 |
47 |
3694,808 |
2894,266 |
По результатам анализа полученных резонансных режимов определено, что все они соответствуют лопаточным формам колебаний.
В рамках дальнейшего анализа конструкции получено относительное распределение динамических напряжений для форм с колебаниями диска. По полученным результатам определены зоны концентрации напряжений. Впоследствии в подобные зоны помещаются тензометрические датчики при проведении испытаний [1].
Заключение
Численное исследование колебаний и вибрационной прочности рабочего колеса является одной из важных задач при проектировании авиационного двигателя.
В процессе решения задачи об оценке динамических характеристик рабочего колеса турбины низкого давления авиационного двигателя получены следующие результаты:
1. Построена конечно-элементная модель рабочего колеса 6 ступени турбины низкого давления авиационного двигателя.
2. Определены собственные частоты и формы колебаний рабочего колеса при заданных условиях работы ТНД.
3. В пакете MATLAB созданы прикладные программы, позволяющие в автоматизированном режиме обрабатывать результаты конечно-элементного моделирования НДС и динамического поведения конструкции, проведенного в пакете ANSYS на основе созданной трехмерной модели рабочего колеса ТНД. Созданные программы могут применяться при исследовании динамических характеристик различных конструкций, при проведении оперативных оценочных расчетов.
4. Построены дисперсионная и резонансные диаграммы, отражающие зависимость собственных частот от количества узловых диаметров и от угловой скорости вращения соответственно.
5. Определены резонансные режимы рабочего колеса, что позволило выявить отсутствие резонансов в дисковых формах колебаний.
6. Определены распределения динамических напряжений при дисковых формах колебаний, которые дают возможность выявить места установки датчиков при проведении экспериментов по определению вибронапряжений на работающем двигателе.
Полученные результаты позволяют произвести подготовку к натурному эксперименту, помогают его спланировать.
Рецензенты:
Домбровский И.В., д.т.н., директор ЗАО «СКБ» ОАО «Мотовилихинские заводы», г. Пермь.
Шевелев Н.А., д.т.н., профессор кафедры «Динамика и прочность машин», проректор по учебной работе ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Библиографическая ссылка
Кухтинский А.Э., Лимонова В.М., Максимов П.В. ОЦЕНКА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК РАБОЧЕГО КОЛЕСА ТУРБИНЫ НИЗКОГО ДАВЛЕНИЯ АВИАЦИОННОГО ДВИГАТЕЛЯ // Современные проблемы науки и образования. 2013. № 4. ;URL: https://science-education.ru/ru/article/view?id=9961 (дата обращения: 31.01.2026).



