Введение
Для погрузочно-разгрузочных и транспортно-складских (ПРТС) работ характерно наличие большого количества отправных и приемных пунктов. Следствием этого является разветвленность транспортных сетей, сопровождающихся формированием некоторого количества дополнительных транспортных пересечений: пункты «хранение», «складирование», «узлы» и «основные устройства», координаты которых являются неизвестными. Грузопоток является основным показателем ПРТС работ, характеризующим процесс перемещения груза не только с количественной, но и с организационной стороны. Затраты на погрузку и разгрузку в основном являются постоянными, тогда в качестве переменной величины выступает транспортное расстояние. Расстояние от пункта отправки до пункта назначения груза существенным образом влияет на технико-экономические и эксплуатационные показатели транспортной сети. Повышение пропускной способности сети определяется количеством грузов, проходящих через рассматриваемый участок в единицу времени, и является основным показателем эффективности работы и позволяет в целом уменьшить эксплуатационные затраты [1; 2].
Исходя из вышеописанного одной из основных задач оптимизации транспортных сетей ПРТС работ является определение кратчайшего пути перемещения и направления грузов от места отправки до места доставки [4].
Одним из вариантов решения поставленной задачи являются геометрические методы построения оптимальной конфигурации инженерных сетей [3; 5], позволяющие использовать единый подход к решению такого класса задач на исходном этапе разработки моделей конфигурации сети. В процессе проектирования транспортных сетей ПРТС работ пункты «хранение», «складирование», «узлы», «оборудование» и «основные устройства» геометрически моделируются точками, а транспортные средства, предназначенные для доставки грузов и связывающие эти пункты, – линиями. Решение сводится к построению кратчайших связывающих линий для заданного множества точек [5].
Преимущества графо-геометрического изображения транспортных сетей ПРТС работ увеличивает наглядность процесса перемещения грузов, помогает проанализировать все этапы работы и выбрать оптимальную конфигурацию сети.
Цель работы: разработать геометрические модели транспортных сетей ПРТС работ на основе построения кратчайших связывающих линий для заданного множества точек плоскости с различной конфигурацией и метрикой, а также методику расчета таких сетей.
Материал и методы исследований: методы оптимизации, инженерные сети, геометрическое моделирование, обобщение построения метода Штейнера.
Результаты и обсуждение
Особенности конфигурации транспортных сетей ПРТС работ заключаются в том, что они зависят от различных факторов, присущих только данной отрасли промышленности. Поэтому важным является технико-экономическое обоснование и планировка транспортных сетей. На этой стадии изучается геометрия трассы для перемещения грузов. Трасса представляется как последовательность отрезков пересекающихся прямых или криволинейных отрезков. Протяженность трассы между отдельными пунктами должна быть минимальной. Элементы трассы должны в полной мере отвечать специфике расположения и движения транспортных средств. Трасса сети в плане представляет собой прямую или ломаную линию. Для установления положения прямых в профиле необходимо иметь данные: отметки начальной и конечной точек, максимальный и минимальный допустимые уклоны трассы. В зависимости от физического пространства приходится рассматривать различные модели сети метрического пространства, соответствующие данному физическому пространству. Для транспортной сети ПРТС работ разработаны и предлагаются следующие модели пространства: евклидова (рис. 1), ортогональная (рис. 2) и полярная (рис. 3).
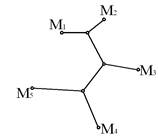
Рис. 1. Евклидова модель
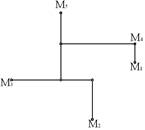
Рис. 2. Ортогональная модель
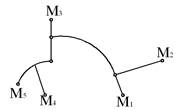
Рис. 3. Полярная модель
Рассмотрим построение приведенных моделей транспортных сетей, связывающих пять заданных пунктов. Для этой цели используем метод Штейнера - в метрическом пространстве требуется построить кратчайшие дерево, вершины которого располагаются в заданных неподвижных точках Мi, требуется определить координаты дополнительно вводимых точек Ni (пересечение отрезков), позволяющих получить более короткую сеть. Ni называют точкой Штейнера, и её положение определяется геометрическими построениями [5]. Необходимые условия и свойства [5; 6], которым должна отвечать кратчайшая связывающая линия на плоскости с евклидовой метрикой: 1) кратчайшая связывающая линия представляет собой дерево, т.е. не имеет замкнутых участков; 2) если точка М является вершиной кратчайшего дерева, то в ней сходятся не более трех отрезков; 3) если из вершины кратчайшего дерева выходят три отрезка, то они образуют между собой углы, равные 120°; 4) если в данной вершине сходятся два отрезка кратчайшего дерева, то угол между ними не может быть меньше 120°; 5) кратчайшая линия, связывающая n точек, имеет не более n-2 точек Штейнера. Необходимые условия и свойства кратчайших отрезков с ортогональной и полярной метрикой сформулированы и приведены в [5; 7]. На основе вышеизложенного для построения оптимальной конфигурации геометрических моделей транспортных сетей ПРТС работ, связывающей заданные пункты погрузки и разгрузки, предлагается следующая методика расчета.
Шаг 1. Заданные пункты сети геометрически моделируются точками.
Шаг 2. В зависимости от рассматриваемого метрического пространства выбирается одна из моделей транспортной сети (рис. 1-3).
Шаг 3. Производится анализ и изучение геометрии трассы сети. В плане ее можно представить прямой, ломаной или кривой линией.
Шаг 4. Для установления положения линии необходимо иметь данные об отметке начальной и конечной точек, максимальный и минимальный допустимый уклон трассы.
Шаг 5. Определяются координаты точек и вычисляются расстояния между ними по формуле:
для евклидовой модели ![]() (1)
(1)
для ортогональной модели ![]() (2)
(2)
для полярной модели
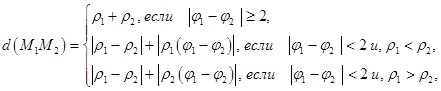 (3)
(3)
где ![]() - декартовы координаты точки
- декартовы координаты точки ![]() ;
;
![]() - декартовы координаты точки
- декартовы координаты точки ![]() ;
;
![]() - полярные координаты точки
- полярные координаты точки ![]() ;
;
![]() - полярные координаты точки
- полярные координаты точки ![]() .
.
Шаг 6. Из множества точек выбираются две точки, расстояние между которыми не больше, чем для любой другой пары. Строится кратчайшее дерево (КД) [5].
Шаг 7. Определяется очередная точка, которая должна быть подключена к дереву.
Шаг 8. После построения КД может возникнуть необходимость соединения на следующем шаге двух КД, дающих начало новой группе соединяемых точек, т.е. образуется новое кратчайшее поддерево. Такие поддеревья дальше должны соединяться между собой на основе принципа наименьшего удлинения КД при каждом отдельном шаге построения.
Шаг 9. В конце получают единственное дерево, связывающее все точки (заданные и точки Штейнера) отрезками.
Шаг 10. Рассчитывают экономическую эффективность путем сравнительно технико-экономического анализа с несколькими вариантами сети, отвечающими наперед заданным требованиям.
Шаг 11. После определения окончательного варианта конфигурации трассы выбирают вид транспорта и определяют основные параметры для укрупненного технико-экономического расчета.
Если в физическом пространстве существует действующая схема транспортной сети, то при помощи данного метода также можно определить кратчайший маршрут перемещения груза с места погрузки в заданный пункт.
Используя геометрические модели, специалист в процессе разработки трассы сети может сочетать данные модели, т.е. получить комбинированные модели сети, отвечающие наперед заданным требованиям.
Выводы
Определение оптимальной конфигурации транспортных сетей ПРТС работ является сложной и многовариантной задачей. Установлено, что транспортное расстояние существенным образом влияет на эксплуатационные затраты. Для определения конфигурации транспортных сетей, имеющей суммарную минимальную длину, предлагаются евклидовы, ортогональные и полярные геометрические модели, т.к. графо-геометрическое изображения транспортных сетей ПРТС работ увеличивают наглядность процесса адресования грузов, помогают специалисту проанализировать все этапы работы и выбрать оптимальную конфигурацию сети. Методика расчета использует принцип наименьшего удлинения [5], позволяющий построить кратчайшие сети в пространствах с различной метрикой.
Рецензенты:
Турдалиев Ауезхан Турдалиевич, доктор технических наук, профессор, директор института промышленной инженерии Казахского национального технического университета имени К.И. Сатпаева, г. Алматы.
Сурашов Нургали Толымбекович, доктор технических наук, профессор, заведующий кафедрой подъемно-транспортных машин и гидравлики Казахского национального технического университета имени К.И. Сатпаева, г. Алматы.
Библиографическая ссылка
Куспеков К.А. РАЗРАБОТКА ГЕОМЕТРИЧЕСКИХ МОДЕЛЕЙ ТРАНСПОРТНЫХ СЕТЕЙ ДЛЯ ПОГРУЗОЧНО-РАЗГРУЗОЧНЫХ И ТРАНСПОРТНО-СКЛАДСКИХ РАБОТ // Современные проблемы науки и образования. 2013. № 4. ;URL: https://science-education.ru/ru/article/view?id=9901 (дата обращения: 13.03.2026).



