Одним из важных направлений деятельности по поддержанию безотказности на заданном уровне является автоматизированная информационная поддержка процессов на всех этапах жизненного цикла локомотивов, в результате которой формируется единое (интегрированное) информационное пространство. Для создания автоматизированных информационных систем, реализующих данные принципы, необходимо сформировать информационные потоки, разработать методики и алгоритмы обработки этой информации. В настоящее время реализации этих задач способствует широкая номенклатура разработанных и внедренных средств контроля и диагностирования основных узлов локомотива, формирующих статистические базы экспериментальных данных. Однако вопрос разработки и внедрения методик и программных продуктов для обработки этих данных до сих пор остается очень актуальным.
Целями данной работы являются исследование статистических зависимостей экспериментальных данных и разработка методики и программного обеспечения для аппроксимации этих зависимостей на примере распределения тока тягового генератора локомотива во времени.
Изложенная в данной статье методика ориентирована на применение в области диагностирования тягового подвижного состава по результатам анализа информации, получаемой от бортовых систем. При разработке использовались исходные экспериментальные данные из архивов, создаваемых аппаратно-программным комплексом «Борт» (АПК «Борт») [5].
Пусть 
– функция изменения тока 
тягового генератора тепловоза во времени 
после переключения контроллера машиниста (далее – КМ) на более высокую позицию (рис. 1, где 1 – кривая изменения тока , 2 – позиция контроллера машиниста 
). Данные, представлены в форме вывода программным обеспечением Kontrol (далее – Kontrol), которое устанавливается на автоматизированном рабочем месте АРМ «Борт» и используется для визуализации информации от АПК «Борт». Оси координат показаны только на графике, а в Kontrol на данный момент не реализуются. Данные для отдельных реализаций изменения тока во времени взяты из статистической базы результатов измерений АПК «Борт» по тепловозам ТЭМ2 приписки эксплуатационного локомотивного депо.
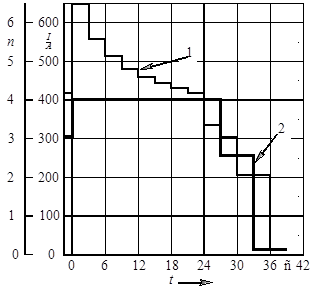
Рисунок 1 – Фрагмент программно визуализированной записи изменения тока генератора и номера позиции КМ
Для разработки методики обработки статистических данных, в первую очередь, необходимо сформировать требования к функции 
, аппроксимирующей экспериментальные данные 
. В данной методике рассматриваются только переходные процессы в зоне уменьшения значений тока тягового генератора после изменения позиции КМ в бо́льшую сторону. Выберем начало координат так, чтобы
, ( 1)
т.е. точкой отсчета по оси абсцисс является момент времени 
, при котором ток, после переключения КМ на более высокую позицию, достиг максимума 
, что определяется по зависимости от номера позиции 
, скоростью движения локомотива 
и нагрузкой на дизель-генераторную установку 
. Значение 
не может стремиться к бесконечности даже при наличии дефектов в соответствующих электрических цепях или нерегламентированных режимах работы потребителей. Поэтому ордината точки пересечения кривой изменения тока должна иметь конечное значение. Это первое требование к функции 
, аппроксимирующей экспериментальные данные 
изменения тока генератора во времени после переключения КМ.
Нагрузкой на тяговый генератор являются тяговые двигатели. Основная особенность электрических двигателей локомотивов в переходных режимах работы – преобладание индуктивной составляющей в полном сопротивлении. В соответствии с законами коммутации [1] ток в индуктивном потребителе не может изменяться скачком или пропадать. Следовательно, второе требование можно сформулировать в следующем виде – в области максимального значения аппроксимирующая функция не должна иметь разрыва.
Критерием предварительной оценки отклонения тока от линейности в функции от времени в переходном режиме может служить коэффициент детерминации 
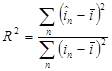, (2)
где
– опытные значения тока в момент времени 
;
– значения тока, полученные из уравнения регрессии;
– среднее значение тока.
Для такой оценки рассмотрены наиболее характерные переходные процессы для каждой позиции КМ (рис. 2). По полученным результатам можно утверждать, что на первой позиции КМ наблюдается отклонение от линейности. На более высоких позициях функция также отклоняется от линейности, но в меньшей степени. Исходя из этого, следует предполагать, что аппроксимирующая функция должна иметь отклонение от линейности или быть нелинейной на всем промежутке времени переходного процесса в отдельной реализации для всех позиций КМ. Это является третьим требованием к функции .
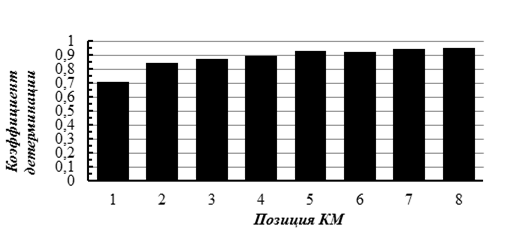
Рисунок 2 – Коэффициент детерминации изменения тока в зависимости от номера позиции КМ
Одним из критериев выбора аппроксимирующей функции является ее кривизна 
на интервале сглаживания экспериментальных данных [1]. По величине и знаку кривизны можно определить направление вогнутости и гладкость исследуемой выборки. Для заданной в явном виде функции 
. (3)
В данном случае производится оценка экспериментальных данных, поэтому необходимо применять численные методы, в соответствии с которыми первая и вторая производные могут быть вычислены с использованием следующих выражений:
, (4)
. (5)
Для оценки кривизны выбраны наиболее характерные записи тока генератора после переключения контроллера в позицию с 1 по 8 соответственно (рис. 3). Критериями выбора конкретной реализации являлись субъективная оценка непрерывности процесса и установившееся значение тока. Очевидно, что длительность переходного процесса на различных позициях КМ различается. Поэтому длительность отдельных реализаций приведена к единому безразмерному отрезку времени 
- такому, что 
.
Анализ полученных результатов (рис. 3) свидетельствует о том, что аппроксимирующая функция должна быть вогнута в сторону начала координат.
Значительные колебания кривизны в области, близкой к 
, объясняются некорректным выбором времени окончания переходного процесса из-за колебаний значения тока на этом участке, что может быть вызвано изменением условий движения, например увеличением сопротивления качения. Таким образом, следующим требованием к 
является вогнутость ее в сторону начала координат.
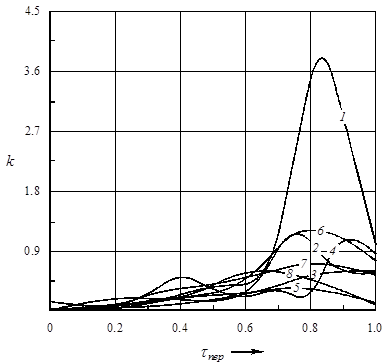
Рисунок 3 – Кривизна экспериментальной функции изменения тока генератора
– приведенное время
Исходя из сформированных требований к аппроксимирующей функции, подобрана функция в виде
, (6)
где
– наименьшее и наибольшее значения тока в одной реализации;
– неизвестные коэффициенты.
Оценка неизвестных коэффициентов может выполняться, в частности, методом наименьших модулей (МНМ) [2]. Использование этого метода уменьшает влияние выбросов в статистической выборке. Влияние, оказываемое крупными остатками на всю сумму, существенно увеличивается при их возведении в квадрат. Если вместо суммы квадратов взять сумму модулей выбросов, влияние остатков на результирующую регрессионную кривую существенно уменьшится [3].
Для применения МНМ необходимо определить начальное значение коэффициентов 
. Функция (6) приводится к виду
, (7)
где
– значения тока, полученные в результате измерения АПК «Борт»;
– время измерения тока в соответствии с условием (1);
– номер измерения в одной реализации.
Используя необходимое число узлов в экспериментальных данных и интерполяционный полином Лагранжа (8) вычисляются начальные значения коэффициентов 6
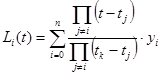. (8)
Дальнейшая реализация метода наименьших модулей заключается в осуществлении итерационного процесса отыскания поправок 
. В ходе этого процесса добиваются минимизации суммы абсолютных значений остаточных невязок 
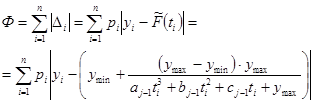, (9)
где
– весовые характеристики отдельного измерения;
– номер шага итерации;
– количество шагов итерации.
Невязки 
(ошибки, погрешности) 
-го измерения находятся из системы уравнений
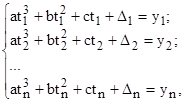. (10 )
Здесь количество уравнений больше числа неизвестных 
и . Решение системы при таких условиях неоднозначно. Если же задать определенные каким-либо образом значения коэффициентов 
, то система (10) принимает вид
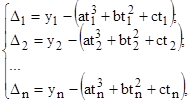, (11)
где
– в этом случае называется остаточной невязкой 
-го измерения.
Решение такой системы ищется в статистическом смысле [2] – подбираются (назначаются) значения неизвестных параметров так, чтобы совокупность невязок обладала бы какими-то минимальными свойствами. Для этого вводится функция 
, зависящая от невязок и от результатов измерения 
. Совокупность подобранных значений 
, при которых 
зависит от вида функции
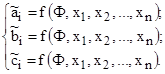(12)
При методе наименьших модулей 
принимается в виде
. (13)
Если в отдельных измерениях различаются ошибки (погрешности), то вводят весовую характеристику
, (14)
Для известных 
находятся поправки , достигая выполнения условия
. (15 )
Система (10) приводится к системе уравнений в поправках , т.е. линеаризуется в окрестностях . Если исследуемая функция непрерывна и дифференцируема в окрестностях 
, то для каждого шага итерации справедливы выражения
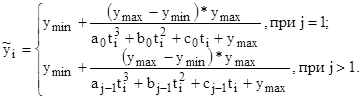(16 )
(17)
( 18 )
( 19 )
( 20 )
Для определения поправок развернем условие (15)
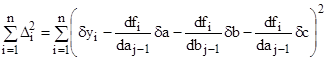. ( 21 )
Влияние отдельных измерений (погрешностей) учитывается весовой характеристикой 
. В работе [2] рекомендовано использовать для вычисления следующую методику
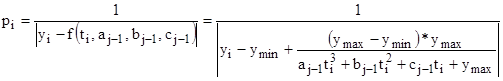(22)
Уравнение (21) принимает вид
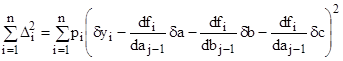(23)
Продифференцировав это уравнение по 
и 
, получают систему уравнений относительно поправок
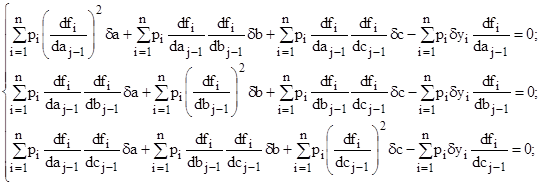(24)
Система (24) – линейная относительно поправок и может быть решена численно методом Гаусса. Полученные значения используются для вычисления новой оценки коэффициентов по (18, 19, 20) для очередного шага итерации.
Методика применена для аппроксимации экспериментальных данных изменения тока тягового генератора во времени (рис. 4). Итерация прекращается при условии
, (25)
где
– малые числа.
Адекватность уравнения регрессии (модели) оценивалась средней ошибкой аппроксимации 
, величина которой не должна превышать 10-12% [4]
, (26)
где
– значение функции, вычисленное с использованием модели (6).
С целью оценки качества аппроксимации, после нахождения коэффициентов , было определено значение отдельных переходных процессов изменения тока генератора на первой позиции для каждого шага итерации. Диапазон изменения средней ошибки аппроксимации – от 10,2 до 1,5% (рис. 5).
После седьмого шага итерации изменение не превышает десятых долей процента, что наряду с (25) может служить критерием окончания процесса аппроксимации.
Средняя ошибка аппроксимации – инструмент для предварительной оценки качества аппроксимации, имеющий низкую чувствительность. Но в связи с тем, что объем статьи не позволяет полностью провести оценку качества аппроксимации, результаты дальнейших исследований в этом направлении будут изложены в следующих публикациях.
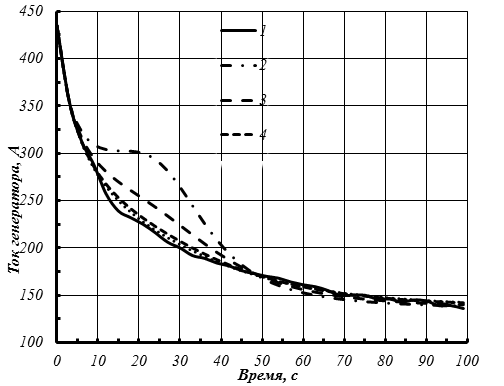
Рисунок 4 – Частный случай аппроксимации одной реализации
1 – исходные данные, соответственно 2, 3, 4 – последовательные четыре итерации
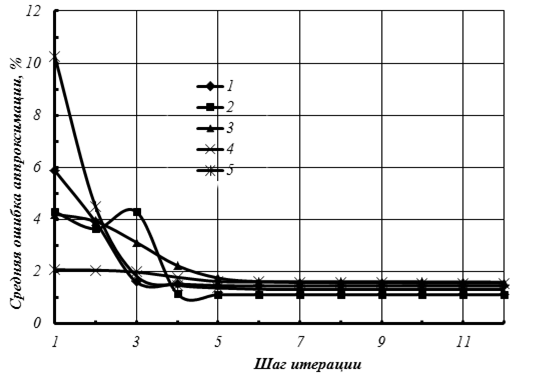
Рисунок 5 – Динамика средней ошибки аппроксимации для пяти отдельных реализаций
В предыдущих публикациях авторами была исследована статистическая информация банка данных, сформированного с использованием АПК «Борт», и предложена методика для отображения времени измерения параметров дизель-генераторной установки маневровых тепловозов ТЭМ2 в едином временном пространстве. Суть выполненных преобразований – перевод информации из одних координат времени в другие, то есть перерасчет реального времени в двенадцатилетний цикл от предыдущего до очередного капитального ремонта. Это позволяет считать одинаковым техническое состояние локомотивов после проведения плановых ремонтов и анализировать совокупность диагностических данных с использованием единой для всех локомотивов точки отсчета изменения технического состояния.
В результате работы была исследована статистическая информация банка данных, сформированного с использованием аппаратно-программного комплекса «Борт», и предложена методика аппроксимации экспериментальных данных изменения тока тягового генератора дизель-генераторной установки маневровых тепловозов ТЭМ2 во времени. В результате проверки данной методики на отдельных реализациях изменения тока тягового генератора во времени была получена кривая, которая может быть использована при диагностировании.
Рецензенты:
Стругов Юрий Федорович, д. ф.-м. н., профессор, ФГБОУ ВПО «Омский государственный университет им. Ф.М. Достоевского» (ОмГУ им. Ф.М. Достоевского), г. Омск.
Матяш Юрий Иванович, д. т. н., профессор, ФГБОУ ВПО «Омский государственный университет путей сообщения» (ОмГУПС (ОмИИТ), г. Омск.
Библиографическая ссылка
Четвергов В.А., Бочаров В.М., Мишин А.И., Гателюк О.В., Сиряк П.А. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ КОНТРОЛЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ЛОКОМОТИВОВ // Современные проблемы науки и образования. – 2013. – № 4. ;URL: https://science-education.ru/ru/article/view?id=9767 (дата обращения: 20.04.2024).