Введение
Если некоторое явление описывается системой дифференциальных уравнений
![]() (1)
(1)
с начальными условиями, которые обычно являются результатами измерений и, следовательно, неизбежно получены с некоторой погрешностью, то естественно возникает вопрос о влиянии изменения начальных значений на искомое решение.
Если окажется, что сколь угодно малые изменения начальных данных способны сильно изменить решение, то решение, определяемое выбранными нами неточными начальными данными, обычно не имеет никакого прикладного значения и даже приближенно не может описывать изучаемое явление.
Если t меняется на конечном отрезке, то ответ на этот вопрос дает теорема о непрерывной зависимости решений от начальных значений. Если же t может принимать сколь угодно большие значения, то этим вопросом занимается теория устойчивости [4; 5].
Известные условия устойчивости и неустойчивости были подробно изучены в работах [1; 2; 4; 5].
1. Понятие об устойчивости решений системы линейных однородных
дифференциальных уравнений первого порядка
Физические процессы часто описываются дифференциальными уравнениями второго и более высокого порядка, которые можно представить в виде системы двух или большего числа линейных дифференциальных уравнений первого порядка. Как говорилось ранее, на физические измерения действуют возмущения, поэтому необходимо знать условия устойчивости решений системы дифференциальных уравнений. В данной статье рассматриваются однородные системы с постоянными коэффициентами (возмущения действуют на коэффициенты).
Определение 1.1 Систему вида
![]() , где
, где 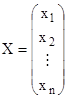 ,
, 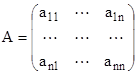 (2)
(2)
будем называть линейной системой однородных дифференциальных уравнений (ОДУ) первого порядка n переменных, где![]() - вещественные постоянные.
- вещественные постоянные.
Теорема 1.1. Линейная однородная система (2) с постоянной матрицей А устойчива тогда и только тогда, когда все характеристические корни ![]() матрицы А обладают неположительными вещественными частями
матрицы А обладают неположительными вещественными частями ![]() , причем характеристические корни, имеющие нулевые вещественные части, допускают лишь простые элементарные делители (т.е. соответствующие клетки Жордана сводятся к одному элементу).
, причем характеристические корни, имеющие нулевые вещественные части, допускают лишь простые элементарные делители (т.е. соответствующие клетки Жордана сводятся к одному элементу).
Теорема 1.2. Линейная однородная система (2) с постоянной матрицей А асимптотически устойчива тогда и только тогда, когда все характеристические корни ![]() матрицы А имеют отрицательные вещественные части
матрицы А имеют отрицательные вещественные части ![]() .
.
Доказательство теорем 1.1 и 1.2 приведено в [4; 5].
2. Устойчивость линейных систем дифференциальных уравнений второго порядка с постоянными коэффициентами
Пусть дана система двух линейных дифференциальных уравнений
![]() , (3)
, (3)
где 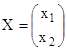 и
и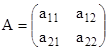 — матрица системы с постоянными коэффициентами. Составим характеристическое уравнение
— матрица системы с постоянными коэффициентами. Составим характеристическое уравнение 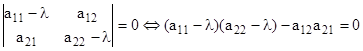 , т.е.
, т.е. ![]() .
.
Введем следующие обозначения: ![]() .
.
Теорема 2.1 (необходимое и достаточное условие устойчивости).
Необходимым и достаточным условием устойчивости нулевого решения системы (3) является положительность введенных коэффициентов ![]() .
.
Доказательство. В данном случае коэффициентами характеристического уравнения являются единица при ![]() и
и ![]() при
при ![]() и
и ![]() соответственно, поэтому необходимым условием устойчивости нулевого решения системы (3) является положительность введенных коэффициентов
соответственно, поэтому необходимым условием устойчивости нулевого решения системы (3) является положительность введенных коэффициентов![]() . Так как матрица Гурвица имеет вид
. Так как матрица Гурвица имеет вид 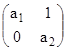 , то условия
, то условия ![]() и
и ![]() также являются и достаточным условием асимптотической устойчивости.
также являются и достаточным условием асимптотической устойчивости.
Замечание 2.1. Путем добавления возмущений каждому из коэффициентов системы исходная система дифференциальных уравнений переходит в некоторую новую систему дифференциальных уравнений, коэффициенты которой можно обозначить ![]() , где
, где ![]() . Изменения коэффициентов могут быть вызваны возмущением характеристик системы. Для возникшей системы верна также теорема 2.1 об устойчивости, что и для исходной с заменой коэффициентов
. Изменения коэффициентов могут быть вызваны возмущением характеристик системы. Для возникшей системы верна также теорема 2.1 об устойчивости, что и для исходной с заменой коэффициентов ![]() на
на ![]() .
.
3. Устойчивость линейных систем дифференциальных уравнений третьего порядка с постоянными коэффициентами
Пусть дана система трех линейных дифференциальных уравнений
![]() , (4) где
, (4) где 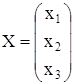 и
и 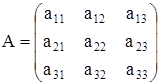 - матрица системы с постоянными коэффициентами. Введем следующие обозначения:
- матрица системы с постоянными коэффициентами. Введем следующие обозначения:
![]() , где в скобках представлена сумма элементов по главной диагонали;
, где в скобках представлена сумма элементов по главной диагонали;
![]() — сумма миноров элементов, стоящих на главной диагонали;
— сумма миноров элементов, стоящих на главной диагонали;
![]() , где
, где ![]() — определитель матрицы А системы.
— определитель матрицы А системы.
Теорема 3.1 (необходимое и достаточное условие устойчивости). Необходимым условием устойчивости нулевого решения системы (4) является положительность всех введенных коэффициентов ![]() . Достаточным условием асимптотической устойчивости является выполнение следующего неравенства:
. Достаточным условием асимптотической устойчивости является выполнение следующего неравенства: ![]() .
.
Доказательство. Для системы дифференциальных уравнений (4) составим характеристическое уравнение:
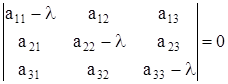 , (5)
, (5)
что после равносильных преобразований запишем в виде:
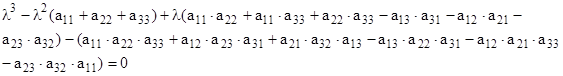
Легко заметить, что коэффициент перед ![]() является определителем матрицы системы (4) со знаком минус, что ранее обозначено через
является определителем матрицы системы (4) со знаком минус, что ранее обозначено через ![]() . Коэффициент перед
. Коэффициент перед ![]() представляет собой сумму миноров к элементам
представляет собой сумму миноров к элементам ![]() , что обозначено через
, что обозначено через ![]() . Коэффициент перед
. Коэффициент перед ![]() является суммой элементов главной диагонали матрицы системы (4) со знаком минус, что обозначено через
является суммой элементов главной диагонали матрицы системы (4) со знаком минус, что обозначено через ![]() . Коэффициент перед
. Коэффициент перед ![]() обозначим через
обозначим через ![]() .
.
Наличие хотя бы одного корня характеристического уравнения с действительной частью больше нуля означает неустойчивость нулевого решения, тогда все корни характеристического уравнения должны иметь отрицательную действительную часть, для чего необходимо, чтобы все коэффициенты характеристического многочлена были положительны. Что и доказывает необходимость в условии теоремы.![]()
Для доказательства достаточности составим матрицу Гурвица для данной задачи, используя введенные обозначения:
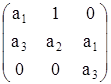 (6)
(6)
Так как ![]() и
и ![]() , то главным условием оказывается следующее неравенство:
, то главным условием оказывается следующее неравенство:
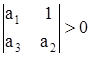 , что равносильно
, что равносильно ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Замечание 3.1. Путем добавления возмущений каждому из коэффициентов системы исходная система дифференциальных уравнений переходит в некоторую новую систему дифференциальных уравнений, коэффициенты которой можно обозначить ![]() , где
, где ![]() . Изменения коэффициентов могут быть вызваны возмущением характеристик системы. Для возникшей системы верна также теорема 3.1 об устойчивости, что и для исходной с заменой коэффициентов
. Изменения коэффициентов могут быть вызваны возмущением характеристик системы. Для возникшей системы верна также теорема 3.1 об устойчивости, что и для исходной с заменой коэффициентов ![]() на
на ![]() .
.
Примером неустойчивой системы дифференциальных уравнений третьего порядка является система вида (4), матрица коэффициентов которой имеет вид 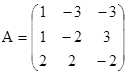 .
.
Несмотря на то что необходимые условия выполняются: ![]() , достаточное условие нарушается.
, достаточное условие нарушается.
Примером устойчивой системы является система, матрица коэффициентов которой имеет вид 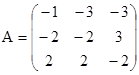 . Для данной системы выполняются и необходимое, и достаточное условия.
. Для данной системы выполняются и необходимое, и достаточное условия.
4. Устойчивость линейных систем дифференциальных уравнений четвертого порядка с постоянными коэффициентами.
Пусть дана система четырех линейных дифференциальных уравнений
![]() , (7) где
, (7) где 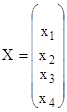 и
и 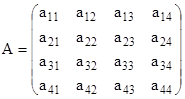 - матрица системы с постоянными коэффициентами. Введем следующие обозначения:
- матрица системы с постоянными коэффициентами. Введем следующие обозначения:
![]() , где в скобках представлена сумма элементов по главной диагонали;
, где в скобках представлена сумма элементов по главной диагонали;
![]()
![]() — сумма миноров элементов, стоящих на главной диагонали со знаком минус;
— сумма миноров элементов, стоящих на главной диагонали со знаком минус;
![]() , где
, где ![]() — определитель матрицы А системы.
— определитель матрицы А системы.
Коэффициент ![]() можно представить в следующем виде:
можно представить в следующем виде:
![]() , где
, где ![]() - определитель матрицы, полученной из матрицы А путем вычеркивания одновременно i-х и j-х строк и столбцов.
- определитель матрицы, полученной из матрицы А путем вычеркивания одновременно i-х и j-х строк и столбцов.
Теорема 4.1 (необходимое и достаточное условие устойчивости).
Необходимым условием устойчивости нулевого решения системы (7) является положительность всех введенных коэффициентов ![]() .
.
Достаточным условием устойчивости является выполнение следующих неравенств:
1) ![]() .
.
2) ![]() . (8)
. (8)
Доказательство проводится аналогичным образом, как и для систем третьего порядка, т.е. путем непосредственного преобразования характеристического уравнения. В силу наличия четырех переменных естественно увеличивается количество условий и усложняется матрица Гурвица, из-за чего появляется среди достаточных второе условие.
Замечание 4.1. Для возмущенных систем четвертого порядка условие устойчивости сохраняет тот же вид, что и в теореме 4.1 с естественным изменением коэффициентов.
Рецензенты:
Расулов Карим Магамедович, д.ф-м.н., профессор Смоленского государственного университета, г. Смоленск.
Мищенко Владимир Ильич, д.т.н., профессор Смоленского государственного университета, г. Смоленск.
Криштоп Виктор Владимирович, д.ф.м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Корея.
Библиографическая ссылка
Конашенко А.В., Родионова Г.С. ОБ УСТОЙЧИВОСТИ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ВТОРОГО ТРЕТЬЕГО И ЧЕТВЕРТОГО ПОРЯДКА // Современные проблемы науки и образования. 2013. № 4. ;URL: https://science-education.ru/ru/article/view?id=9669 (дата обращения: 13.03.2026).



