Введение
Современные компактные датчики атмосферного давления на основе MEMS-технологий нашли применение в самых различных областях. Наиболее широко распространены датчики атмосферного давления, встраиваемые в современные сотовые телефоны.
Используемые в авиации инерциальные системы навигации [6] позволяют рассчитывать оценку локации объекта (в том числе и высоту полета), отклонение которой от истинного положения без корректировки увеличивается с течением времени. Применение атмосферных датчиков давления позволяет значительно повысить точность определения высоты полета [7], хотя в силу изменчивости атмосферного давления в долгосрочном периоде абсолютную высоту можно измерять, только используя дополнительные данные, например от GPS-модулей.
Для ряда приложений точного определения абсолютной высоты не требуется. В таких случаях достаточно зафиксировать лишь изменение положения объекта по высоте. В [11] авторы оценивают точность определения фактов падения людей при ходьбе на основе резких отклонений в показаниях датчиков давления. Такие системы позволяют медицинскому персоналу быстрее оказывать помощь людям в специальных учреждениях. Подобные системы относятся к классу приложений, использующих шаблоны поведения человека при ходьбе [10]. Датчики давления, закрепленные на теле человека и используемые совместно с датчиками ускорения, значительно повышают точность определения высоты положения человека при ходьбе, а также при перемещениях между этажами по сравнению с использованием только датчиков ускорения [5]. В [5; 8] авторы анализируют точность определения относительной высоты, используя датчик с заранее известной высотой (опорный датчик). Высота рассчитывается по разнице между показаниями давления опорного датчика и датчика, закрепленного на объекте (мобильный датчик).
Поскольку датчики измеряют давление с некоторой погрешностью, а атмосферное давление с течением времени меняется, то вычисление абсолютной высоты всегда сопряжено с ошибками.
Использование показаний от одного опорного и одного мобильного датчиков с целью определения относительной высоты положения последнего возможно только при соответствующем усреднении показаний. Однако при усреднении за большой период времени точность определения высоты может ухудшиться: сглаживание показаний может нивелировать резкие изменения положения датчика по высоте. Дополнительным ограничением при использовании усредненных показаний является энергопотребление. Чем больше данных используется для усреднения за один и тот же период времени, тем больше энергозатрат требуется на получение соответствующих показаний. Это особенно критично при использовании мобильных датчиков с автономным питанием.
Использование данных от акселерометра, гироскопа и/или магнетометра незначительно улучшает точность определения высоты, поскольку точность у датчиков давления выше, чем у остальных [8]. Существенно повысить точность можно, используя несколько опорных датчиков атмосферного давления.
Предложенный в работе способ расчета оценки высоты датчика основан на усреднении данных от нескольких опорных датчиков давления. В работе приводятся результаты расчета высоты положения датчика при различном количестве данных и различном количестве датчиков. Выполнен анализ причин отклонения скорости уменьшения эмпирической дисперсии оценки высоты при увеличении количества данных по сравнению с теоретической дисперсией; построена соответствующая модель. В заключение приводятся: способ расчета доверительного интервала оценки используемой для расчета высоты положения датчика, результаты расчетов дисперсии при различном количестве показаний датчиков и способ выбора оптимального набора датчиков для расчета наилучшей в определенном смысле оценки неизвестной высоты.
Методы
Описание системы сбора данных
Для сбора данных о давлении использовались девять устройств системы RealTRACTM [9]. Из них восемь стационарных устройств Access Point (рисунок 1) и одно мобильное устройство RIO (рисунок 2).

Рис. 1. Стационарное устройство Access Point, используемое в качестве опорного датчика

Рис. 2. Мобильное устройство RIO, оснащенное датчиком давления
Основное назначение стационарных устройств Access Point – формирование зоны покрытия беспроводной сети, объединение проводного и беспроводного сегментов сети и передача данных от мобильных устройств на сервер. Также данные устройства используются в качестве стационарных реперных точек с заранее известными трёхмерными координатами для определения местоположения мобильных устройств RIO.
Во все устройства встроен цифровой датчик давления BMP085 производства компании Bosch Sensortec. BMP085 основан на пьезорезистивной технологии и имеет высокую точность, линейность показаний и термостабильность. Разрешающая способность датчика 1 Па. Значения абсолютной и относительной точности измерения давления при различных внешних условиях показаны в таблице 1 [3].
|
|
Внешние условия |
Значение в гПа |
|
Абсолютная точность |
700 — 1100 гПа 0 — +65 °С |
+/- 1,0 |
|
300 — 700 гПа 0 — +65 °С |
+/- 1,0 |
|
|
300 — 1100 гПа -20 — 0 °С |
+/- 1,5 |
|
|
Относительная точность |
700 — 1100 гПа 25 °С |
+/- 0,2 |
|
0 — 65 °С p = const |
+/- 0,5 |
|
Таблица 1. Значения абсолютной и относительной точности показаний датчика BMP085 при различных внешних условиях.
Датчик может работать в различных режимах внутреннего усреднения. Эти режимы и соответствующие им среднеквадратические отклонения приведены в таблице 2 [3].
|
Режим |
Количество значений для усреднения |
Уровень среднеквадратического отклонения в Па |
|
низкое энергопотребление |
1 |
6 |
|
стандартный |
2 |
5 |
|
высокое разрешение |
4 |
4 |
|
сверхвысокое разрешение |
8 |
3 |
Таблица 2. Уровень среднеквадратического отклонения для различных режимов внутреннего усреднения.
При нормальных условия работы все устройства системы RealTRACTM периодически считывают показания датчика с заданной частотой сэмплирования, производят перерасчет значений внутренних регистров датчика в абсолютное давление в паскалях и отправляют результат на сервер. Стоит отметить, что во всех экспериментах, приведенных в данной статье, используется более точный алгоритм расчета абсолютного давления с вещественными числами [4], а не рекомендуемый производителем [3]. Использование вещественных чисел позволяет избежать ошибок округления, свойственных целочисленной арифметике.
Система RealTRACTM, кроме прочего, позволяет вычислять 3D-локацию мобильных радиоустройств в зданиях, используя измерения расстояний методом Time-Of-Flight (TOF) и измерения встроенных датчиков [1; 2]. Как показано в [12], датчики давления могут быть использованы для определения этажа в многоэтажных зданиях.
В данной работе анализируется использование информации только от датчиков давления, без комбинирования ее с данными систем локации, построенных на иных принципах.
При проведении экспериментов опорные устройства были закреплены в здании на различных заранее известных высотах. Мобильное устройство находилось внутри здания на неизвестной высоте. Давление в устройствах измерялось с точностью до десятых долей Паскаля с частотой 1 Гц в течение 60 минут. Моменты времени и результаты считывания показаний с датчиков фиксировались на сервере в регистрационных файлах для последующего анализа. Такая схема с централизованным характером хранения информации применялась, поскольку в долгосрочном периоде внутренние часы устройств быстро расходятся, и синхронность снятия показаний перестает соблюдаться.
Все девять устройств, находящихся на одной высоте, имели разные, фиксированные погрешности в абсолютных измерениях. Для наглядности на рисунке 3 представлены показания датчиков давления от двух стационарных устройств, размещенных рядом на одной высоте. На рисунке приведен типичный разброс данных при достаточно стабильном атмосферном давлении за период около 20 минут. Смещение по оси ординат среднего значения показаний каждого датчика связано с недостаточной точностью измерения абсолютного давления (±100 Па). При использовании подобных датчиков в составе работающей системы локаций необходимо выполнять предварительную калибровку показаний для каждого отдельного устройства, т.е. определить величину смещения каждого датчика относительно остальных.
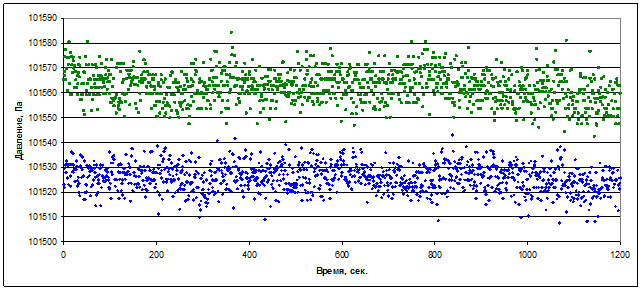
Рис. 3. Пример показания двух датчиков давления за период около 20 минут.
Оценка высоты по давлению
Поскольку датчики измеряют атмосферное давление с некоторой погрешностью, то можно рассматривать показания датчиков как случайные процессы. Оценку неизвестной высоты мобильного устройства и ее точность можно рассчитать, используя предложенную ниже стохастическую модель и соответствующие методы прикладной статистики.
Пусть ![]() датчиков измеряют атмосферное давление в моменты времени
датчиков измеряют атмосферное давление в моменты времени ![]() . Датчик
. Датчик ![]() закреплен на высоте
закреплен на высоте ![]() относительно некоторой точки с высотой
относительно некоторой точки с высотой ![]() (начала отсчета). Мы полагаем, что датчики откалиброваны относительно друг друга, а давление с ростом высоты уменьшается линейно с коэффициентом
(начала отсчета). Мы полагаем, что датчики откалиброваны относительно друг друга, а давление с ростом высоты уменьшается линейно с коэффициентом ![]() . Точная формула вычисления высоты по показаниям датчиков:
. Точная формула вычисления высоты по показаниям датчиков:
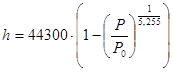 ,
,
где ![]() КПа [10]. В случае небольшого диапазона изменения давления (при абсолютных давлениях
КПа [10]. В случае небольшого диапазона изменения давления (при абсолютных давлениях ![]() КПа) допущение о линейности
КПа) допущение о линейности ![]() от
от ![]() справедливо.
справедливо.
Обозначим через ![]() – показание датчика
– показание датчика ![]() в момент времени
в момент времени ![]() . Значения показаний датчиков можно представить в следующем виде:
. Значения показаний датчиков можно представить в следующем виде:
![]() ,
,
где ![]() – значение атмосферного давления в точке начала отсчета высоты (
– значение атмосферного давления в точке начала отсчета высоты (![]() ) в момент времени
) в момент времени ![]() ,
, ![]() – случайная величина, равная погрешности показаний датчика
– случайная величина, равная погрешности показаний датчика ![]() в момент времени
в момент времени ![]() .
.
Исследование показаний датчиков показало, что погрешности измерений ![]() нельзя рассматривать как независимые случайные величины. Это связано с наличием не контролируемой систематической погрешности датчиков, которая проявляется в виде автокорреляции значений показаний (см. далее раздел Результаты экспериментов). Поэтому будем предполагать, что для каждого
нельзя рассматривать как независимые случайные величины. Это связано с наличием не контролируемой систематической погрешности датчиков, которая проявляется в виде автокорреляции значений показаний (см. далее раздел Результаты экспериментов). Поэтому будем предполагать, что для каждого ![]() случайные величины
случайные величины ![]() зависимы, но имеют одинаковую функцию распределения с нулевым математическим ожиданием. Чем больше интервал времени между двумя измерениями, тем слабее связь между ними. Поэтому будем считать, что ковариации случайных величин
зависимы, но имеют одинаковую функцию распределения с нулевым математическим ожиданием. Чем больше интервал времени между двумя измерениями, тем слабее связь между ними. Поэтому будем считать, что ковариации случайных величин ![]() для каждого
для каждого ![]() зависят от разностей моментов времени:
зависят от разностей моментов времени:
![]() .
.
Кроме того, считаем, что ![]() и
и ![]() независимы
независимы ![]() и любых
и любых ![]() и
и ![]() .
.
Обозначим ![]() . Таким образом,
. Таким образом, ![]() – значения показания датчика
– значения показания датчика ![]() в момент времени
в момент времени ![]() , если бы он находился на высоте
, если бы он находился на высоте ![]() .
.
Пусть имеется еще один датчик, высота которого ![]() не известна, но имеются его показания в моменты времени
не известна, но имеются его показания в моменты времени ![]() . Будем рассматривать эти показания как случайный процесс
. Будем рассматривать эти показания как случайный процесс ![]() , где
, где ![]() ,
, ![]() – погрешность показания в момент времени
– погрешность показания в момент времени ![]() . Случайные величины
. Случайные величины ![]() также имеют одинаковую функцию распределения с нулевым математическим ожиданием и ковариацией, зависящей от разностей моментов времени:
также имеют одинаковую функцию распределения с нулевым математическим ожиданием и ковариацией, зависящей от разностей моментов времени:
![]() .
.
Кроме того, считаем ![]() независимыми от
независимыми от ![]() при любых
при любых ![]() в момент времени
в момент времени ![]() . Введем обозначение для разницы между показаниями мобильного датчика и стационарного датчика
. Введем обозначение для разницы между показаниями мобильного датчика и стационарного датчика ![]() в момент времени
в момент времени ![]() :
:
![]() .
.
Очевидно, что ![]() – случайные величины, которые для каждого
– случайные величины, которые для каждого ![]() имеют одинаковую функцию распределения. Поскольку математическое ожидание величин
имеют одинаковую функцию распределения. Поскольку математическое ожидание величин ![]() и
и ![]() равно нулю, то математическое ожидание всех
равно нулю, то математическое ожидание всех ![]() равно
равно ![]() . Очевидно, что определение величины
. Очевидно, что определение величины ![]() позволит определить неизвестную высоту
позволит определить неизвестную высоту ![]() . Поэтому следует ограничиться задачей определения оценки для
. Поэтому следует ограничиться задачей определения оценки для ![]() , поскольку из характеристик этой оценки можно без труда определить характеристики
, поскольку из характеристик этой оценки можно без труда определить характеристики ![]() .
.
В качестве оценки ![]() можно использовать
можно использовать ![]() :
:
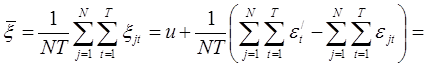
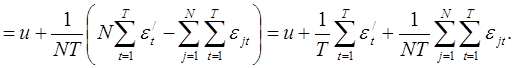 (1)
(1)
Поскольку математическое ожидание величин ![]() равно
равно ![]() , то
, то ![]() , откуда следует несмещенность оценки
, откуда следует несмещенность оценки ![]() .
.
Дисперсия ![]() равна:
равна:
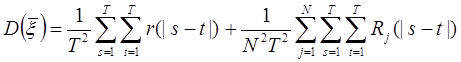 .
.
Обозначим:
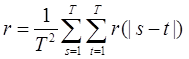 ,
, 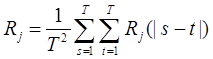 .
.
Тогда формула для дисперсии ![]() упрощается:
упрощается:
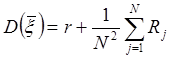 . (2)
. (2)
Усредняя по времени (![]() ) и по датчикам (
) и по датчикам (![]() ) зарегистрированные разницы между показаниями датчиков
) зарегистрированные разницы между показаниями датчиков ![]() , получаем оценку для
, получаем оценку для ![]() (формула 1). Дисперсия этой оценки определяет точность расчета
(формула 1). Дисперсия этой оценки определяет точность расчета ![]() для заданных
для заданных ![]() и
и ![]() , поэтому ее можно использовать для построения доверительного интервала оценки. Также можно найти оценку математического ожидания и доверительный интервал для
, поэтому ее можно использовать для построения доверительного интервала оценки. Также можно найти оценку математического ожидания и доверительный интервал для ![]() .
.
Результаты экспериментов
Для расчетов оценки (1) и ее дисперсии (2) использовались показания девяти опорных датчиков и одного мобильного датчика за 60 минут, полученные из регистрационных файлов центрального сервера (см. выше Описание системы сбора данных). На рисунке 4 приведен график выборочной автокорреляционной функции ![]() разницы показаний двух датчиков, рассчитанной следующим образом. Пусть
разницы показаний двух датчиков, рассчитанной следующим образом. Пусть ![]() и
и ![]() – выборка показаний первого и второго датчиков. Обозначим разницы между показаниями
– выборка показаний первого и второго датчиков. Обозначим разницы между показаниями ![]() в моменты измерений
в моменты измерений ![]() . Для каждого
. Для каждого ![]() оценка автокорреляции
оценка автокорреляции ![]() рассчитывалась по формуле выборочного коэффициента корреляции между выборками
рассчитывалась по формуле выборочного коэффициента корреляции между выборками ![]() и
и ![]() . Для всех значений
. Для всех значений ![]() коэффициент корреляции значимо отличался от нуля.
коэффициент корреляции значимо отличался от нуля.
На рисунке 4 ось абсцисс соответствует ![]() – интервалу между измерениями показаний датчиков, ось ординат –
– интервалу между измерениями показаний датчиков, ось ординат – ![]() . Из графика видно, что значение автокорреляции медленно уменьшается с увеличением
. Из графика видно, что значение автокорреляции медленно уменьшается с увеличением ![]() , это связано с наличием автокорреляции у ошибок измерений
, это связано с наличием автокорреляции у ошибок измерений ![]() .
.
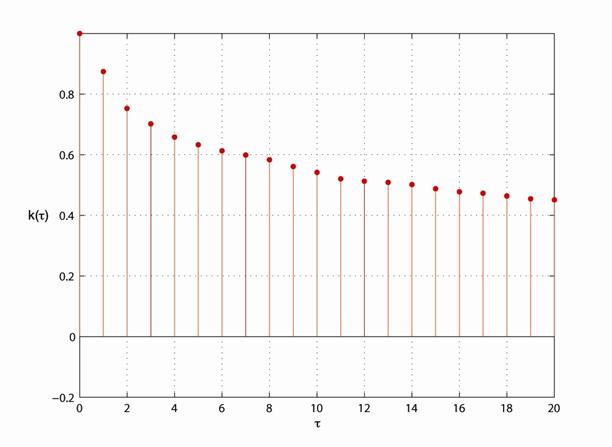
Рис. 4. Оценка автокорреляции ![]() разницы показаний двух датчиков, где
разницы показаний двух датчиков, где ![]() – интервал между моментами времени, когда измерялись разницы показаний
– интервал между моментами времени, когда измерялись разницы показаний
Кроме того, был рассчитаны значения оценок среднеквадратического отклонения ![]() при различных
при различных ![]() и
и ![]() (таблица 3).
(таблица 3).
|
|
|
|
|
|
|
|
|
|
|
|
|
8,17 |
7,08 |
6,66 |
6,47 |
6,32 |
6,24 |
6,21 |
6,16 |
6,13 |
|
|
4,44 |
3,70 |
3,45 |
3,35 |
3,25 |
3,22 |
3,24 |
3,21 |
3,18 |
|
|
3,66 |
3,04 |
2,79 |
2,69 |
2,60 |
2,57 |
2,58 |
2,55 |
2,52 |
|
|
3,25 |
2,71 |
2,45 |
2,35 |
2,23 |
2,21 |
2,22 |
2,19 |
2,16 |
|
|
3,07 |
2,58 |
2,30 |
2,21 |
2,10 |
2,07 |
2,09 |
2,06 |
2,03 |
|
|
2,95 |
2,48 |
2,16 |
2,07 |
1,96 |
1,92 |
1,94 |
1,92 |
1,88 |
|
|
2,80 |
2,36 |
2,06 |
1,96 |
1,85 |
1,83 |
1,85 |
1,82 |
1,79 |
Таблица 3. Оценка ![]() при различных
при различных ![]() и
и ![]()
Например, если с каждого из трех датчиков взять по 24 показания и усреднить их, то получаем оценку среднеквадратического отклонения (СКО), равную 2,45 Па, что соответствует ширине доверительного интервала, равной 38 см при оценке высоты мобильного датчика с надежностью 0,95.
Актуальной является задача о том, какой набор показаний дает оценку с большей точностью при фиксированном ![]() . Если использовать большие
. Если использовать большие ![]() , то будет задействовано больше устройств. Если использовать большие
, то будет задействовано больше устройств. Если использовать большие ![]() , то мы можем столкнуться с ограничениями, описанными во введении (нечувствительность к изменениям высоты мобильного датчика или энергопотребление). Рассмотрим значения оценок для
, то мы можем столкнуться с ограничениями, описанными во введении (нечувствительность к изменениям высоты мобильного датчика или энергопотребление). Рассмотрим значения оценок для ![]() при различных комбинациях числа датчиков
при различных комбинациях числа датчиков ![]() и числа показаний
и числа показаний ![]() от каждого датчика при фиксированном общем числе показаний
от каждого датчика при фиксированном общем числе показаний ![]() (таблица 4).
(таблица 4).
|
Число Датчиков |
Число Показаний Каждого Датчика |
Оценка Среднеквадратического Отклонения |
Общее Число Показаний
|
|
1 |
8 |
4,44 |
8 |
|
8 |
1 |
6,16 |
|
|
1 |
16 |
3,66 |
16 |
|
2 |
8 |
3,70 |
|
|
1 |
24 |
3,25 |
24 |
|
3 |
8 |
3,45 |
|
|
1 |
32 |
3,07 |
32 |
|
2 |
16 |
3,04 |
|
|
4 |
8 |
3,35 |
|
|
1 |
40 |
2,95 |
40 |
|
5 |
8 |
3,25 |
|
|
1 |
48 |
2,80 |
48 |
|
2 |
24 |
2,71 |
|
|
3 |
16 |
2,79 |
|
|
6 |
8 |
3,22 |
Таблица 4. Оценка ![]() при фиксированном
при фиксированном ![]()
Из таблицы 4 видно, что при одном и том же общем числе показаний датчиков СКО почти всегда увеличивается с ростом числа датчиков ![]() и уменьшением
и уменьшением ![]() . Следовательно, бóльшая точность определения локации мобильного датчика в среднем получается путем увеличения числа
. Следовательно, бóльшая точность определения локации мобильного датчика в среднем получается путем увеличения числа ![]() усредняемых показаний одного датчика, а не увеличением общего числа датчиков
усредняемых показаний одного датчика, а не увеличением общего числа датчиков ![]() при фиксированном количестве показаний
при фиксированном количестве показаний ![]() . Поскольку в некоторых случаях СКО все же больше, чем при меньшем
. Поскольку в некоторых случаях СКО все же больше, чем при меньшем ![]() при фиксированном
при фиксированном ![]() (см., например, СКО для
(см., например, СКО для ![]() ,
, ![]() ), то актуальной является задача определения подмножества датчиков для наилучшего усреднения (и дальнейшего определения неизвестной высоты положения датчика) при фиксированном числе показаний
), то актуальной является задача определения подмножества датчиков для наилучшего усреднения (и дальнейшего определения неизвестной высоты положения датчика) при фиксированном числе показаний ![]() .
.
Оптимальное количество опорных датчиков
Для определения оптимального количества опорных датчиков ![]() , используемых для расчета оценки неизвестной высоты положения датчика (1), введем дополнительное обозначение для усредненной разницы между показаниями
, используемых для расчета оценки неизвестной высоты положения датчика (1), введем дополнительное обозначение для усредненной разницы между показаниями ![]() -го стационарного и мобильного датчиков:
-го стационарного и мобильного датчиков:
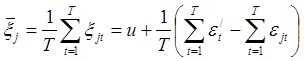 .
.
Дисперсия этой величины:
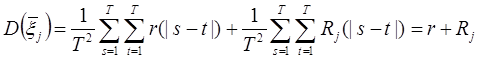 .
.
Рассмотрим задачу выбора подмножества ![]() стационарных датчиков, для которых дисперсия разности их усредненного показания и показания мобильного датчика будет минимальной:
стационарных датчиков, для которых дисперсия разности их усредненного показания и показания мобильного датчика будет минимальной:
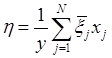 ,
,
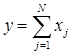 ,
,
![]() ,
,
![]() .
.
где ![]() – количество выбранных датчиков,
– количество выбранных датчиков, ![]() – признак включения датчика в набор
– признак включения датчика в набор ![]() .
.
Очевидно, что
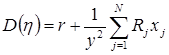
Пусть датчики упорядочены по возрастанию дисперсии усредненной ошибки ![]() :
:
![]() .
.
Последовательно увеличивая количество задействованных датчиков ![]() , вычисляя среднее значение разностей между стационарными датчиками и мобильным
, вычисляя среднее значение разностей между стационарными датчиками и мобильным
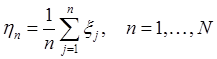 ,
,
а также его дисперсию
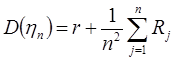 ,
,
можно найти оптимальное ![]() , дающее минимум этой дисперсии:
, дающее минимум этой дисперсии:
![]() .
.
Найденное значение ![]() определяет оптимальный набор датчиков
определяет оптимальный набор датчиков ![]() .
.
Иными словами, использование данных, полученных от датчиков из набора ![]() , влечет минимум дисперсии разницы между усредненными показаниями стационарных и мобильных датчиков, а, следовательно, и дисперсии оценки искомой высоты положения датчика.
, влечет минимум дисперсии разницы между усредненными показаниями стационарных и мобильных датчиков, а, следовательно, и дисперсии оценки искомой высоты положения датчика.
Если нам известны лишь значения ![]() , но не известны
, но не известны ![]() , то из (2) следует, что сортировка датчиков по возрастанию величины
, то из (2) следует, что сортировка датчиков по возрастанию величины ![]() приведет нас к упорядочению датчиков по возрастанию
приведет нас к упорядочению датчиков по возрастанию ![]() .
.
Предложенный алгоритм может быть использован в real-time системах для выбора оптимального количества опорных датчиков для получения наиболее эффективной оценки неизвестной высоты положения мобильного датчика.
Заключение
Представленные в работе формулы позволяют рассчитывать оценку неизвестной высоты мобильного устройства и определять для нее доверительный интервал, используя данные нескольких опорных датчиков давления ![]() за некоторый период времени
за некоторый период времени ![]() . Определив по некоторой заранее полученной выборке значения дисперсии для различных
. Определив по некоторой заранее полученной выборке значения дисперсии для различных ![]() и
и ![]() и задав желаемый доверительный интервал, можно использовать соответствующие значения
и задав желаемый доверительный интервал, можно использовать соответствующие значения ![]() и
и ![]() в последующих расчетах. В зависимости от конечной задачи и существующих ограничений можно для заданного доверительного интервала выбрать наиболее подходящую пару
в последующих расчетах. В зависимости от конечной задачи и существующих ограничений можно для заданного доверительного интервала выбрать наиболее подходящую пару ![]() . Показано, что, несмотря на то, что в среднем увеличение
. Показано, что, несмотря на то, что в среднем увеличение ![]() предпочтительнее увеличения
предпочтительнее увеличения ![]() при фиксированном
при фиксированном ![]() , в некоторых случаях увеличение
, в некоторых случаях увеличение ![]() приводит к увеличению доверительного интервала, а, следовательно, к уменьшению точности рассчитываемой оценки высоты. Оптимальное количество датчиков зависит от дисперсий показаний каждого из датчиков. Так, при большой дисперсии, использование показаний соответствующего датчика дополнительно к показаниям остальных может увеличить дисперсию оценки высоты. Предложен алгоритм выбора оптимального набора опорных датчиков для расчета оценок неизвестной высоты датчиков.
приводит к увеличению доверительного интервала, а, следовательно, к уменьшению точности рассчитываемой оценки высоты. Оптимальное количество датчиков зависит от дисперсий показаний каждого из датчиков. Так, при большой дисперсии, использование показаний соответствующего датчика дополнительно к показаниям остальных может увеличить дисперсию оценки высоты. Предложен алгоритм выбора оптимального набора опорных датчиков для расчета оценок неизвестной высоты датчиков.
Оценка высоты, рассчитываемая по данным датчиков давления, может быть использована для уточнения локации мобильного устройства в системах локального позиционирования в многоэтажных зданиях [12]. В качестве продолжения данной работы можно провести количественный анализ повышения точности локации за счет использования датчиков давления.
Рецензенты:
Печников Андрей Анатольевич, доктор технических наук, доцент, ведущий научный сотрудник Лаборатории телекоммуникационных систем Института прикладных математических исследований Карельского научного центра Российской академии наук, г. Петрозаводск.
Рогов Александр Александрович, доктор технических наук, профессор, заведующий кафедрой теории вероятностей и анализа данных математического факультета Петрозаводского государственного университета, г. Петрозаводск.
Библиографическая ссылка
Воронов Р.В., Волков А.С., Региня С.А., Федоров А.А., Мощевикин А.П., Волков А.С., Региня С.А., Федоров А.А., Мощевикин А.П. МЕТОД ОБРАБОТКИ ДАННЫХ РАСПРЕДЕЛЕННОЙ СЕТИ ДАТЧИКОВ ДАВЛЕНИЯ ДЛЯ ОЦЕНКИ ОТНОСИТЕЛЬНОЙ ВЫСОТЫ МОБИЛЬНОГО УЗЛА // Современные проблемы науки и образования. 2013. № 4. ;URL: https://science-education.ru/ru/article/view?id=9631 (дата обращения: 14.02.2026).



