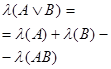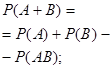Введение. Стохастическая содержательно-методическая линия, сравнительно недавно введенная в школьный курс математики, занимает в нем особо важное место, так как, с одной стороны, является неотъемлемой составляющей «реальной» математики, а с другой – обладает уникальным потенциалом для реализации объективно существующих внутрипредметных связей [3, гл.1, п.9, с. 53-56]. В свою очередь, реализация таких связей способствует формированию у учащихся целостного представления о математике как науке, «переносу» знаний и умений из одного раздела изучаемой дисциплины в другой, порождает возможности использования математических методов и алгоритмов в новых условиях [5].
С этой точки зрения, наиболее плодотворным здесь является этап обобщающего повторения и, в частности, подготовки к ЕГЭ, который в наибольшей степени отвечает цели расширения, обобщения, систематизации и углубления знаний, установления тех связей и отношений между элементами знаний, которые не были раскрыты ранее.
Целью настоящей работы является изложение технологических приемов решения вероятностных задач на основе использования логических операций над высказываниями и свойств этих операций, а идейная основа приемов заложена в общности свойств функции истинности и вероятности (определенных на соответствующих булевых алгебрах). Предлагаемые приемы мы относим к технологическим, поскольку они обладают такими признаками технологий обучения, как целенаправленность, планируемость и проектируемость, научная обоснованность, воспроизводимость и гарантированность результата; они (приемы) позволяют, в частности,
1) классифицировать задачи на основе определенных признаков;
2) алгоритмизировать их решение;
3) предложить формулы для действия в рамках определенных вероятностных схем.
1. Действия над событиями и логические операции. Стохастический материал интегрирует в себе три следующих блока содержания (раздела курса математики): «Элементы комбинаторики», «Элементы теории вероятностей», «Введение в математическую статистику». Следовательно, уже сам по себе этот материал предполагает наличие внутрипредметных связей. Центральным и образующим основные связи в содержании стохастического материала является понятие вероятности. Речь идет о количественном выражении степени объективной возможности наступления того или иного случайного события. Вероятность как функция, определяемая на алгебре событий, в учебных задачах представлена тремя следующими моделями: классическая вероятность, относительная частота события (статистическая вероятность) и геометрическая вероятность. Общей для этих моделей является постановка задачи о нахождении вероятности «составного» события, в том случае, когда известны (или могут быть найдены) вероятности взаимодействующих событий – «компонентов».
Обсуждаемые внутрипредметные связи и предлагаемые нами технологические приемы базируются на следующих теоретических положениях [1], относящихся к алгебрам Буля.
1.1. Алгебра событий, алгебра высказываний и алгебра всех подмножеств данного множества являются примерами булевых алгебр с одной унарной и двумя бинарными операциями (представленными ниже в таблице соответствия п. 2) .
1.2. Выделенные в булевых алгебрах элементы 0 и 1 могут быть интерпретированы в алгебре событий как, соответственно, события достоверное Е и невозможное Ø
, а в алгебре высказываний – как тождественная истина Е и тождественная ложь Ø.
1.3. Бинарные операции над элементами в каждой из указанных алгебр подчинены ряду свойств (аксиом), среди которых присутствуют свойства коммутативности, ассоциативности, а также дистрибутивности каждой из бинарных операций по отношению к другой.
1.4. На булевой алгебре может быть определено отображение в промежуток [0,1], которое, в частности, на множестве всех высказываний есть функция истинности
а на множестве событий есть вероятность Р.
1.5. Операции умножения событий 
и конъюнкция высказываний 
имеют один и тот же словесный аналог «и А, и В» (наступление и события А и события В – истинность и высказывания А и высказывания В).
1.6. Операция сложения событий А+В и дизъюнкция высказываний 
имеют один и тот же словесный аналог «хотя бы одно из А и В» ( «или А, или В, или и А, и В» – истинность или высказывания А или высказывания В или их обоих).
Мы считаем полезным выделить случай сложения несовместных событий и в этом случае использовать термин «альтернативная сумма» и применять обозначение 
(совпадающее с обозначением альтернативной дизьюнкции в алгебре высказываний). Альтернативная сумма и альтернативная дизъюнкция событий и высказываний, соответственно, обладают одним и тем же словесным аналогом «или А, или В».
1.7. «Не А» служит одновременно словесным аналогом как операции перехода к событию 
, противоположному А, так и операции отрицания высказывания А.
2. Технологические приемы. В следующей технологической таблице представлены связи между тремя интерпретациями булевых алгебр (см. п. 1.1), а также между функцией истинности высказывания А (состоящего в том, что событие А наступает) и вероятностью события А.
Таблица соответствия операций в булевых алгебрах
|
|
Операция над событиями |
Логический аналог |
Теоретико- множественный аналог |
Функция истинности высказывания |
Вероятность события |
|
1 |
Переход к
противопо-ложному событию |
Отрицание вания А |
Дополнение ко множеству А |
|
|
|
2 |
Произведение событий
|
|
Пересечение множеств А и В |
|
где |
|
3 |
Сумма событий А+В |
|
Объединение множеств А и В |
|
в частности,
|
есть условная вероятность события В
Термином «технологическая таблица» мы подчеркиваем, что представленная в ней информация может быть напрямую использована для реализации следующих технологических приемов:
1) интерпретации действий над событиями диаграммами Вьена;
2) формализации доказательств свойств этих действий с помощью таблиц истинности, построенных для соответствующих «составных» высказываний (см. пп. 1.1–1.7);
3) выбора формулы для вычисления вероятности «составного» события в случае, когда известны вероятности событий-«компонентов».
Следующий пример демонстрирует, как может быть применен второй из указанных приемов (см. также [2]).
Доказать, что событие, противоположное наступлению хотя бы одного из данных событий, равносильно ненаступлению обоих данных событий.
В формализованном виде имеем так называемый закон де Моргана
, (2.1)
и теперь достаточно установить соотношение
, в справедливости которого убеждаемся, сравнив пятый и седьмой столбцы следующей таблицы истинности (
.
Таблица истинности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i+j-ij |
|
)
)
)
)
Из сотношения (2.1), в свою очередь, вытекает следующая формула для вычисления вероятности наступления хотя бы одного из данных совместных событий:
. (2.2)
3. Схема альтернатив. Решение многих задач основано на следующей альтернативе, к которой часто сводятся составные события: «или и А и В, или не А и С», которую мы выделяем как отдельную вероятностную схему и называем схемой альтернатив. События, укладывающиеся в эту схему, могут быть представлены в виде 
. Следовательно,
, (3.1)
где 
; при этом вероятности 
и 
событий В и С, соответственно, могут быть как «безусловными», так и условными: 
. Формула альтернатив (3.1) включает в себя формулу полной вероятности для двух гипотез
(3.2)
и формулу вычисления вероятности наступления только одного из двух независимых событий А и В
, где 
. (3.3)
4. Алгоритм. В качестве одного из технологических приемов теперь может быть предложен следующий пошаговый алгоритм (технологическая карта) решения задач на нахождение вероятности составного события.
Шаг 1. Ввести в рассмотрение (и обозначить) событие, вероятность которого требуется определить.
Шаг 2. Выразить это события через более простые с помощью словесных аналогов соответствующих логических операций (см. п. 1, 1.5–1.7).
Шаг 3. Ввести в рассмотрение (и обозначить) события-компоненты, которые «задействованы» в операциях на шаге 2.
Шаг 4. Записать выражение составного события через введенные события-компоненты с помощью операций отрицания (перехода к противоположному событию), сложения, умножения событий (формализация результата, полученного на шаге 2) .
Шаг 5. Применить соответствующую формулу; см. правый столбец таблицы соответствия п. 2, или формулы альтернатив (3.1) – (3.3).
Шаг 6. Произвести вычисления.
Замечание. В процессе решения конкретных задач иногда отдельные шаги удобно поменять местами.
5. Примеры. Рассмотрим использование вышеприведенных технологических приемов на примерах, аналогичных заданиям п. В 10 открытого банка задач ЕГЭ по математике [4].
Пример 1. Вероятность того, что завтра на маршрут выйдут не больше 20 автобусов, равна 0,25, а вероятность того, что автобусов будет меньше 15, равна 0,1. Какова вероятность, что на маршрут выйдут от 15 до 20 автобусов.
Вводимые в рассмотрение события (шаги 1 и 3 алгоритма): А – автобусов от15 до 20 (его вероятность подлежит отысканию) и «сопутствующие» события: В – автобусов не более 20, С – меньше 15 автобусов на маршруте. В соответствии со вторым шагом алгоритма, событие В состоит в наступлении или А, или С, т.е. (шаг 4) 
. Следовательно (шаги 5 и 6), 
или 
, откуда 
.
Пример 2. Двор дома освещается фонарём с двумя лампами, параллельно соединенными. Вероятность перегорания каждой лампы в течение года равна 0,1. Найдите вероятность того, что 1) в течение года фонарь будет освещать двор; 2) к концу года в фонаре будет гореть только одна лампа.
Для ответа на первый вопрос воспользуемся алгоритмом п. 4.
Шаг 1. Событие А – фонарь будет освещать двор.
Шаг 2. Событие А равносильно исправности хотя бы одной из ламп (или первой, или второй, или обоих).
Шаг 3. Вводим события 
и 
– исправность первой и второй ламп, соответственно.
Шаг 4. В соответствии с шагом 2 и 1.7 представляем событие А в виде 
.
Шаг 5. Выбираем для расчетов формулу (2.2): 
Р
(случай
совместных независимых событий).
Шаг 6. 
.
Второй вопрос задачи предполагает использование схемы альтернатив: событие В, состоящее в исправности только одной из ламп, представимо в виде «или и не или не и ». Имеем, по условию, 
.
В соответствии с (3.3) получаем 
Пример 3. Компьютерной диагностике подвергается группа участников диспансеризации, среди которых 10 % страдают некоторыми заболеваниями. В результате диагностики болезнь выявляется с вероятностью 0,95, и с вероятностью равной 0,03 здоровый участник признается больным. Какова вероятность, что произвольно выбранного протестированного участника компьютер признает заболевшим?
Решение. Если событие D состоит в том, что протестированный участник признан больным, то (шаги 1–4 алгоритма п. 4) наступление D означает, что больным признан либо здоровый (событие А) , либо больной (событие 
) член группы: «или А и D , или не А и D». Следовательно (шаг 5), имеем формулу альтернатив в виде (3.2). В нашем случае 
)
, и 
.
Выводы. Предлагаемые новые технологические приемы решения вероятностных задач основаны на использовании логических операций над высказываниями, позволяющих «опознать» стандартную вероятностную схему (вероятность суммы, произведения, схема «альтернатив») и выбрать соответствующую формулу для вычисления вероятности.
Результаты работы могут быть использованы педагогами на этапе обобщающего повторения курса математики и, в частности, в процессе подготовки к ЕГЭ.
Рецензенты:
Богословский Андрей Витальевич, доктор технических наук, профессор, профессор кафедры «Высшая математика» ФГБОУ ВПО «Тамбовский государственный технический университет», г. Тамбов.
Куликов Геннадий Михайлович, доктор физико-математических наук, профессор, заведующий кафедрой «Прикладная математика и механика» ФГБОУ ВПО «Тамбовский государственный технический университет», г. Тамбов.
Библиографическая ссылка
Нахман А.Д. ТЕХНОЛОГИЧЕСКИЕ ПРИЕМЫ РЕШЕНИЯ ВЕРОЯТНОСТНЫХ ЗАДАЧ // Современные проблемы науки и образования. – 2013. – № 3. ;URL: https://science-education.ru/ru/article/view?id=9613 (дата обращения: 14.12.2024).