Введение
Пусть имеется производственное нормальное качество – каждый произведенный объект удовлетворяет стандарту с вероятностью, близкой к единице. При длительном производстве объектов со временем происходит сбой оборудования (постепенный или резкий), что влечет за собой снижение производственного качества. При обнаружении снижения качества контроль останавливается, происходит переналадка оборудования или его замена, то есть восстанавливается качество производства, и контроль возобновляется вновь, без какого-либо учета произошедших событий.
Правила остановки контроля как рекуррентные события
В [2; 4] было показано, что правило остановки контроля [1; 3; 5] можно интерпретировать как рекуррентное событие E, которому соответствует некоторый конечный набор состояний A1, A2, …, AN , а математическое ожидание проконтролированных объектов до наступления события E равно:
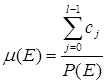, (1)
где A1, A2, …, AN - состояния, соответствующие событию Е; 
- максимальная длина состояния, соответствующего событию Е; сh – вероятность перехода за h шагов из состояний A1, A2, …, AN , соответствующих событию Е, в эти же состояния.
Результаты
Правило остановки П2 формулируется так: «из последних r1 объектов – k1 дефектных объектов или из последних r2 объектов – k2 дефектных объектов», где r2>r1, k2>k1 и k1>1. При этом полагают, что вероятность каждого объекта быть годным равна p и быть дефектным равна q=1-p.
Рассмотрим классический случай контроля, т.е. случай, когда информация о контроле после наступления остановки обнуляется. Для правил остановки контроля П2 положим, что k2/(k1–1) – целое число (при k=2 число всегда будет целым), и опишем все состояния отвечающие наступлению события 
- правилу остановки контроля «из последних r1 объектов – k1 дефектных объектов или из последних r2 объектов – k2 дефектных объектов».
Сначала выделим состояния, которые соответствуют наступлению события: «из последних r1 объектов k1 объектов дефектных». А именно это состояния:
.
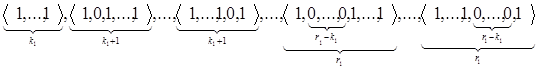Далее необходимо выписать состояния, отвечающие наступлению события: «из r2 (r2>r1) последних объектов k2 (k2>k1) объектов дефектных». Заметим, что для наступления такого события состояние, отвечающее ему, может иметь не более чем (k1–1) подряд единиц. В противном случае ранее наступило бы событие: из последних r1 объектов k1 дефектных. Кроме того, между соседними группами из i и j единиц, если i+j ≥ k1 должна быть группа не менее чем из (k1–t) нулей, где t=max (i;j). Теперь, учитывая, что k2/(k1–1) – целое число, будем полагать его равным k0. Таким образом, минимальную длину, равную
,
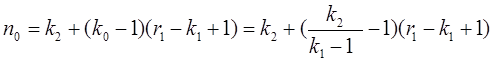будет иметь следующее состояние
,
где k0 групп из (k1–1) единиц и (k0–1) группа из (r1–k1+1) нулей. Ясно, что длину, равную
,
имеют следующие состояния:
.
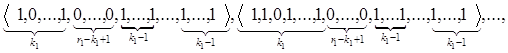
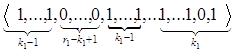Продолжая рассуждать так и далее, установим, что максимальную длину, равную r2, имеют такие состояния:
.
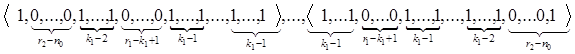Тогда вероятность наступления события 
равна сумме вероятностей вышеописанных состояний:
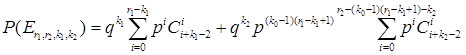. (2)
Далее зафиксируем k1=2 (при этом k0 – целое число) и вычислим 
- вероятность наступления события 
:
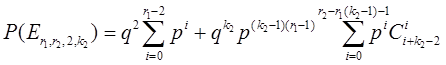. (3)
Теперь необходимо найти 
. Для этого заметим следующее. Основание «1» входит в любое состояние, соответствующее событию и с0=1. Тогда нетрудно видеть, что
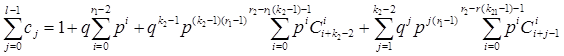. (4)
Действительно, первое слагаемое отражает тот факт, что с0=1, второе и третье слагаемое отражают вероятность перехода в состояние, соответствующее событию из основания «1». Четвертое слагаемое это сумма вероятностей перехода в состояние, соответствующее событию из оснований, отличных от основания «1».
Таким образом, получаем математическое ожидание числа проконтролированных объектов до остановки контроля по правилу «из последних r1 объектов 2 дефектных объекта или из последних r2 объектов k2 дефектных объекта»:
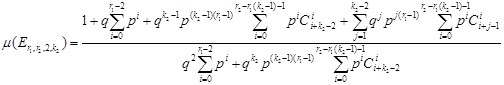. (5)
Фактически была доказана следующая теорема.
Теорема. Математическое ожидание числа проконтролированных объектов до остановки контроля при классическом контроле по правилу «из последних r1 объектов 2 дефектных объекта или из последних r2 объектов k2 дефектных объекта» при q – вероятности дефектности каждого объекта и p=1-q - вероятности годности каждого объекта выражается формулой (5).
Таблица
Таблица 1. Математическое ожидание числа проконтролированных объектов до наступления остановки по правилу «из последних 
объектов – 
объектов дефектных или из последних 
объектов – 
объектов дефектных» для 
, 
, 
и набора значений p – вероятности объекта быть годным
|
|
p=0,5 |
p=0,6 |
p=0,7 |
p=0,8 |
p=0,85 |
p=0,9 |
p=0,95 |
p=0,96 |
p=0,97 |
p=0,98 |
p=0,99 |
p=0,995 |
|
r2=15 |
5,1 |
6,9 |
10,2 |
17,6 |
26,8 |
51,2 |
179,1 |
276,1 |
489,0 |
1113,5 |
4620,2 |
19092,3 |
|
r2=20 |
5,1 |
6,9 |
10,0 |
16,5 |
24,0 |
43,4 |
143,5 |
220,1 |
390,8 |
906,4 |
3971,8 |
17357,4 |
|
r2=25 |
5,1 |
6,9 |
10,0 |
16,0 |
22,6 |
38,9 |
119,9 |
181,3 |
318,5 |
738,5 |
3342,5 |
15380,1 |
|
r2=40 |
5,1 |
6,9 |
10,0 |
15,7 |
21,2 |
33,3 |
86,2 |
123,9 |
206,4 |
455,1 |
2048,7 |
10225,7 |
|
r2=80 |
5,1 |
6,9 |
10,0 |
15,7 |
21,0 |
31,5 |
65,6 |
86,4 |
128,5 |
244,3 |
914,1 |
4318,3 |
Заключение
Основной результат, полученный в работе для правила остановки контроля «из последних r1 объектов 2 дефектных объекта или из последних r2 объектов k2 дефектных объекта» для классического контроля, сформулирован в виде теоремы.
Правила остановки контроля для плана непрерывного контроля, в который они входят, играют существенную роль. На практике, применяя какие-либо правила остановки контроля, поступают следующим образом. Если реально проконтролированное число объектов до остановки контроля меньше математического ожидания числа проконтролированных объектов для фиксированного 
(вероятности годности объекта, т.е. для нормального хода производства объектов), то принимаются какие-либо меры для восстановления нормального хода производства. Это может быть замена или переналадка производственного оборудования в условиях поточного производства объектов или проведение профилактических мер при контроле показателей здоровья населения. Если же реально проконтролированное число объектов до остановки контроля равно или больше математического ожидания числа проконтролированных объектов для фиксированного , то контроль продолжается без принятия каких-либо мер.
Рецензенты:
Пенский Олег Геннадьевич, доктор технических наук, доцент, профессор кафедры процессов управления и компьютерной безопасности, Пермский государственный национальный исследовательский университет, г. Пермь.
Ясницкий Леонид Нахимович, доктор технических наук, профессор, заведующий кафедрой прикладной информатики, Пермский государственный гуманитарно-педагогический университет, г. Пермь.
Библиографическая ссылка
Гусев А.Л. СЛОЖНЫЕ ПРАВИЛА ОСТАНОВКИ НЕПРЕРЫВНОГО КОНТРОЛЯ // Современные проблемы науки и образования. – 2013. – № 4. ;URL: https://science-education.ru/ru/article/view?id=9605 (дата обращения: 19.04.2024).