Введение
Мотивация и успех в получении профессионального образования, а также удовлетворенность в дальнейшем профессиональной деятельностью в большей степени определяется осознанным выбором вуза для получения этого образования. Предпрофильное и профильное обучение школьников, реализующее идеи личностно-ориентированного образования, позволяет учащимся оценить степень адекватности своих претензий, их способности и возможности к получению конкретного образования, повышает осознанность сделанного выбора, снижает риск ошибочных решений.
Образование сегодня, в том числе и на этапе профильного обучения, должно учитывать социокультурные условия, связанные с ускоряющейся и углубляющейся изменчивостью мира, обозначающие ситуацию неопределенности, ставя перед образованием инновационную задачу формирования человека, способного не только решать стоящие сегодня проблемы, но и быть готовым к решению проблем еще не сформулированных. Очевидно, что традиционная система образования, ориентированная на передачу устоявшихся знаний, не способна выполнить поставленную задачу. Нужен новый подход к решению этой задачи, актуальной для педагогической теории и образовательной практики, в том числе и на этапе профильного обучения. Такой подход авторы связывают с реализацией так называемого опережающего обучения, рассматривающего субъект учебной деятельности в постоянном развитии своих способностей и возможностей, в том числе и освоения новых способов деятельности. Для нас ценно мнение П. М. Новикова и В. М. Зуева, определяющих опережающее образование как развитие способности личности действовать в режиме «постоянного обновления существующего состояния» [5]. Другими словами, опережающее образование ориентируется на формирование человека, интеллектуальные и личностные качества и способности которого позволяют ему продуктивно решать проблемы в условиях неопределенности, прогнозировать результат и последствия своей деятельности, неся ответственность за нее. Потенциал математики в условиях личностно-ориентированного образования позволяет развивать такую личность.
Этап профильного обучения школьников, сензетивность подросткового возраста к изменениям создают условия для реализации идей опережающего образования. В качестве теоретических предпосылок опережающего обучения выступают исследования ученых, занимающихся развивающим обучением (А. Дистерверг, И. Г. Песталоцци, К. Д. Ушинский, В. В. Давыдов, П. Я. Гальперин, Л. В. Занков, Э. В. Ильенков, А. Н. Леонтьев, Н. А. Менчинская, С. Л. Рубинштейн, Д. Б. Эльконин).
Направленность на развитие учащихся как главную цель педагогической системы, опираясь на исследования Л. В. Занкова, В. В. Давыдова, Д. Б. Эльконина и других ученых, позволяет выделить принципы опережающего (ориентированного на развитие) обучения, главными из которых являются: ведущая роль теоретического знания; обучение на высоком уровне сложности; высокий темп прохождения учебного материала.
Для обогащения содержания профильных дисциплин, преподаваемых на углубленном уровне в рамках Целевой программы «Организация эффективного взаимодействия Сибирского федерального университета и ОАО «ГМК «Норильский никель» на 2011-2015 годы», авторы данной статьи базировались на следующих принципах:
1. В программу дополнительного образования включались разделы учебного материала, сложные для усвоения школьниками («Текстовые задачи», «Рациональные уравнения и системы уравнений», «Рациональные и иррациональные неравенства»).
2. Углубленно изучались разделы школьного курса, входящие в структуру единого государственного экзамена («Текстовые задачи», «Рациональные уравнения и системы уравнений», «Рациональные неравенства и системы неравенств», «Элементарные функции, их свойства. Построение графиков функций», «Производная функции и ее приложения»).
3. Обеспечивалась преемственность между программами довузовского и вузовского образования («Элементы векторной алгебры», «Производная функции и ее приложения»).
Выбор педагогических технологий для реализации идей опережающего образования, ориентированного на развитие интеллектуальных и личностных способностей субъекта образовательного процесса, определяется возможностью обеспечивать это развитие, а именно: проблемным построением учебной информации; вариативностью на уровнях: методов и форм организации познавательной деятельности; содержания и структуры учебного материала в соответствии с учебными возможностями обучающихся; целей и задач учебных дисциплин; дифференцированным направлением учебной деятельности (одаренных учащихся; учащихся, способных к освоению программы материала; учащихся, требующих особого внимания и поддержки); диалоговыми и фасилитационными формами организации образовательного процесса.
Педагогическое обеспечение опережающего образования определило необходимость:
1. Обогащения содержания учебным материалом, ориентированным на развитие возможностей и способностей обучающихся в ситуации успешной образовательной деятельности.
2. Структурирования содержания учебного материала как ориентировочной основы образовательной деятельности на основе выявления опорных единиц учебного содержания как эффективного способа компоновки учебного материала для организации опережающего обучения с выделением блока повышенного уровня сложности.
3. Соотнесения содержания и целей выявленных опорных единиц учебного материала с возможностями использования вариативных процессуальных технологий: проблемного обучения, задачного подхода, ТРИЗ, методики решения исследовательских задач и др.
4. Разработки сценариев занятий и их содержания с использованием процессуальных педагогических технологий.
5. Разработки опорных схем, конспектов, таблиц, чертежей, рисунков и других средств, основанных на феномене идентификации образа (зрительного, звукового, смыслового) и текста, представляющего содержание учебного материала.
Опыт нашей педагогической деятельности показал высокую эффективность использования опорных схем, конспектов, сигналов в повышении качества усвоения учебного материала по математике в дополнительном образовании на этапе профильного обучения. Мы соглашаемся с мнением И. Я. Каплуновича, определяющего визуализацию как базовое условие для возникновения понимания. Человек считает, что понимает какой-то процесс, если он может построить зрительную модель этого процесса. Иными словами, правильные действия, процедуры, равно как и варианты «неправильных», т.е. возможных ошибок, должны быть показаны в образной форме – в виде схем, рисунков, видео, анимации, мультимедийных модельных сценариев [2].
Опорный сигнал понимается нами как блок (модуль) учебного материала, логически связанный с другими, подкрепленный ассоциациями, легко воспроизводимый, усиленный образностью и цветом. Опорные схемы позволяют сконцентрировать внимание учащихся на самом главном, подчеркнуть связи, способствовать систематизации учебной информации.
При разработке опорной схемы (контекста) нами учитывались основные принципы ее составления: лаконичность (300–400 печатных знаков); структурность (4–5 связок, логических блоков); смысловой акцент (рамки, отделение блоков); унификация знаков; автономность (4–5 блоков, объединенных в самостоятельную структуру); ассоциативность; доступность воспроизведению; цветовая наглядность и образность.
Нарушение этих принципов существенно снижает эффективность использования опорных схем. Здесь важно подчеркнуть роль опорных сигналов в обобщении и систематизации учебной информации. Однако в большей степени эти функции (систематизации и обобщения) выполняет структурно-логическое представление учебного материала. Каждая новая тема в профильном обучении начиналась с представления учащимся структурной схемы содержания учебного материала, подлежащего усвоению, с обозначением отдельных модулей и разделов. Эта схема выполняет ориентирующую роль и задает динамическую модель развития учебной деятельности по освоению этого учебного материала, упорядочивает, рационализирует и повышает ее эффективность. Учебная информация, подлежащая усвоению в учебной деятельности, может быть представлена системой взаимосвязанных и взаимовлияющих друг на друга модулей, последовательность освоения которых осуществляется в логике освоения знаний: восприятия, понимания, осмысления, запоминания, применения, обобщения, систематизации. Определение взаимосвязанных и взаимовлияющих друг на друга модулей позволяет исследовать отношения между ними, установить причинно-следственные связи, что ориентирует на формирование теоретического мышления. Исходя из этого, В. В. Давыдов и Д. Б. Эльконин свою концепцию развивающего обучения связывают, прежде всего, с содержанием учебных предметов и логикой (способами) его развертывания в учебном процессе [1].
Предъявляя учащимся опорные сигналы, структурно-логические схемы, необходимо обучать их умению структурировать учебный материал. Актуальность формирования умений структурировать учебный материал определяется тем, что это умение многофункционально, надпредметно, междисциплинарно, многомерно и поэтому может быть определено как метаумение. Умение структурировать учебный материал является метаумением, характеризующим интеллектуальную деятельность учащегося по представлению изучаемого учебного материала в виде целостной структуры на основе выбранного принципа, в результате которой достигается качественно иное, более глубокое системное знание [6]. Важно, что структурирование учебного материала приводит учащихся к осмыслению темы, осознания целей и задач обучения, что фактически позволяет выстраивать ориентированную основу учебной деятельности. Приобретению учащимися опыта выстраивать ориентированную основу учебной деятельности способствует разработка алгоритмов решения математических задач.
Рассмотрение важности дополнительных занятий по математике в условиях профильного обучения определено системообразующей, методологической ролью фундаментальных знаний в содержании образования, определяющих условие преодоления «догоняющего» характера образования. Именно качество фундаментальных знаний позволит в дальнейшем человеку понимать и быстро осваивать новые технологии, новые функции. Содержание математики создает условия для развития мыслительных способностей, таких как: наблюдение и сравнение (сопоставление), абстрагирование и конкретизация, обобщение и специализация, классификация и систематизация, анализ и синтез, отыскание и применение аналогий и противопоставлений, построение гипотез и планирование действий, развитие критического отношения к изучаемому материалу и самоконтроль. Указанные умения и навыки важны не только сами по себе, а как объективные условия целеустремленного, продуктивного мышления, ведущего к решению поставленных задач [7]. Приведем примеры развития мышления в курсе математики. Наблюдение и сравнение, являясь эмпирическими методами познания действительности, позволяют сделать вывод об общих закономерностях по нескольким частным случаям. Такая мыслительная операция как абстрагирование позволила вскрыть глубинную общность, выявить общие черты при определении базовых понятий математики: «число», «величина», «множество», «геометрическая фигура», «алгебраическое выражение», «функция» и другие понятия. Совершенно очевидно, что каждая задача особенна с точки зрения конкретности и специфичности заданного условия. Необходимо отвлечься от ее особенностей, чтобы выбрать прием решения, а лишь затем учесть эти особенности при осуществлении действий этого приема. В ходе решения различных задач нами формируются умения учащихся выявлять в различных задачах единую математическую схему их решения. Это способствует овладению общими методами решения задач и формирует высокий уровень абстрагирования.
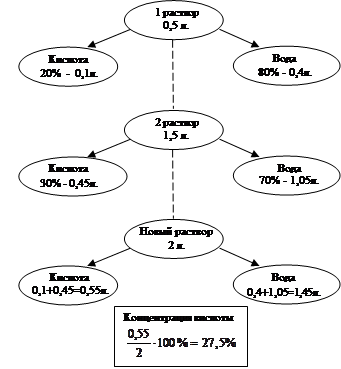
Представим опорный сигнал для решения конкретной задачи: имеется два кислотных раствора: один – 20 %, другой – 30 %. Из 0,5л. первого раствора и 1,5л. второго раствора образовали новый раствор. Какова концентрация кислоты в новом растворе (в процентах)?
Известно, что в разных областях знаний используется разный конкретный смысл математических понятий. В частности, производная в механике конкретизируется как скорость прямолинейного движения, в теории электричества – как сила тока, в теории теплопередачи – как перепад температур, в химии – как скорость химической реакции, скорость радиоактивного распада и т.п. Переход от абстрактных понятий к их конкретным воплощениям или с переходом от данного абстрактного понятия к менее абстрактным понятиям выступает противоположностью абстрагирования и развивает конкретизацию как мыслительную операцию.
Математика как учебная дисциплина имеет мощный потенциал для развития способности к обобщению. Обобщение позволяет осуществлять переход от двумерного пространства (плоскости) к трехмерному, а затем и к бесконечномерному евклидову пространству.
Путем абстрагирования от тех или иных свойств мы приходили к определенным понятиям. Важным этапом мыслительной деятельности учащихся является изучение сформированного понятия, а именно как необходимых, так и достаточных признаков для него, установление связей с другими понятиями, классификация и т.д. Понимание различия между необходимыми и достаточными условиями является важным этапом развития мыслительной деятельности учащихся в курсе школьной математики. Отработка необходимых и достаточных условий существования экстремума функции позволяет сформировать эту мыслительную деятельность.
Важным этапом математического мышления является специализация понятия. Например, с помощью специализации из общего понятия последовательности выделяется арифметическая прогрессия, геометрическая прогрессия, возрастающая последовательность, убывающая последовательность, сходящаяся последовательность, ограниченная последовательность и т.д. Если для выделения частных случаев в некотором понятии используют различные значения некоторого признака, то осуществляется операция классификация. Например, если признаком является число сторон у многоугольника, то множество всех прямоугольников распадается на классы треугольников, четырехугольников, пятиугольников Классификация понятия облегчает его изучение, позволяя во многих случаях сводить дело к изучению отдельных классов, составляющих в своей совокупности это понятие.
Обозначив потенциал содержания математического образования в развитии мыслительных способностей учащихся профильных классов, определим педагогические технологии и методы обучения, направленные на активизацию познавательной деятельности учащихся, развитие их творческих способностей.
Одним из таких методов обучения является проблемное обучение. Разработкой психологических, дидактических основ проблемного обучения занимались многие известные психологи (Скаткин М. И., Кудрявцев Т. Е., Лернер И. Я., Махмутов М. И. и т. д.). «Проблемное обучение заключается в создании перед учащимися проблемных ситуаций, в осознании, принятии и разрешении этих ситуаций учащимися в ходе совместной деятельности учащегося с учителем при оптимальной самостоятельности первых и под общим руководством последнего» [4]. При проблемном изложении – знания не сообщаются в готовом виде, а становятся проблемой, создается проблемная ситуация, преподаватель побуждает искать пути разрешения, порождается процесс разрешения противоречий между познанным и непознанным, между знанием и неумением применить его на практике, появляется познавательный практический поиск, тем самым приобретаются новые знания.
Развитие творческих способностей учащихся профильных классов в контексте опережающего обучения определяет необходимость активизации самостоятельной исследовательской деятельности. Понятно, что на этапе профильного обучения учащиеся еще не способны получить значимый научный результат, но субъективно новый продукт исследовательской деятельности должен быть ее результатом. Здесь возникает проблема выбора тем научно-исследовательской работы, которая могла бы быть по силам учащимся профильных классов, интересна им, имела бы профильную направленность. Нам представляется целесообразным формулировать темы исследовательских работ, предполагающие проведение компьютерных, численных экспериментов.
Реализация стратегии опережения в условиях профильного обучения школьников математике предполагает педагогическое обеспечение комплексом заданий разного типа и уровня, поэтапно развивающих мыслительную деятельность учащихся. Преподаватели СФУ, участвующие в сетевом проекте профильного обучения «НорНикель-классов», разработали комплексы заданий по темам «Элементы векторной алгебры», «Текстовые задачи», «Рациональные уравнения и системы уравнений», «Иррациональные уравнения и системы уравнений», «Рациональные и иррациональные неравенства», «Элементарные функции, их свойства. Построение графиков функций», «Производная и ее приложения».
Апробация этих заданий показала существенное повышение мотивации к обучению математике и качества знаний по дисциплине.
Рецензенты:
Гафурова Наталья Владимировна, доктор педагогических наук, профессор, профессор кафедры педагогики профессионального обучения, проректор по учебной работе ФГАОУ «Сибирский федеральный университет» Министерство образования и науки РФ, г. Красноярск.
Игнатова Валентина Владимировна, доктор педагогических наук, профессор, зав. кафедрой психологии и педагогики ФГБОУ BIIO «Сибирский государственный технологический университет», г. Красноярск.
Библиографическая ссылка
Осипова С.И., Терещенко Ю.А., Климович Л.В. СТРАТЕГИИ ОПЕРЕЖЕНИЯ В УСЛОВИЯХ ПРОФИЛЬНОГО ОБУЧЕНИЯ ШКОЛЬНИКОВ МАТЕМАТИКЕ // Современные проблемы науки и образования. 2013. № 3. ;URL: https://science-education.ru/ru/article/view?id=9601 (дата обращения: 22.02.2026).



