Введение
Под планом непрерывного контроля [1, 3, 5] понимается совокупность правил контроля и действий, которые направлены на обнаружение снижения производственного качества продукции и принятия мер по нормализации производства. Такие планы контроля используют правила остановки контроля типа «из последних r объектов – k дефектных» 
целые числа, 
. При использовании таких планов после остановки контроля предполагается, что происходит переналадка оборудования или его замена и контроль возобновляется заново без учета результатов контроля предыдущих объектов производства.
Этот процесс можно интерпретировать так. Имеется производственное нормальное качество – каждый произведенный объект удовлетворяет стандарту с вероятностью близкой к единице. При длительном производстве объектов со временем происходит сбой оборудования, что влечет за собой снижение производственного качества. При обнаружении снижения качества контроль останавливается, происходит переналадка оборудования или его замена, то есть восстанавливается качество производства, и контроль возобновляется вновь, без какого-либо учета произошедших событий.
При контроле риска здоровью населения подобной замены оборудования не может быть. При остановке контроля в этом случае принимаются меры по снижению риска для здоровья населения. Однако меры действуют не мгновенно, а в течение некоторого времени. Для учета этого обстоятельства в работах [2, 4] был предложен новый подход, названный непрерывным статистическим контролем с памятью. Его отличие от классического плана контроля состоит в том, что после остановки последний результат контроля запоминается, и возобновление контроля происходит не с нуля, а с учетом предшествующего события.
Правила остановки контроля как рекуррентные события
В [2, 4] было показано, что правило остановки контроля можно интерпретировать как рекуррентное событие E, которому соответствует некоторый конечный набор состояний A1, A2, …, AN , а математическое ожидание проконтролированных объектов до наступления события E равно:
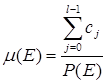, (1)
где A1, A2, …, AN – состояния, соответствующие событию Е; 
– максимальная длина состояния, соответствующего событию Е; сh – вероятность перехода за h шагов из состояний A1, A2, …, AN , соответствующих событию Е, в эти же состояния.
Основные результаты
Правила остановки контроля П1 используются для планов непрерывного контроля по альтернативному признаку. Вероятность каждого объекта быть годным равна p и быть дефектным равна q=1-p. Далее годный объект будем обозначать «0», а дефектный объект – «1».
Рассмотрим классический случай контроля, т.е. случай, когда информация о контроле после наступления остановки обнуляется. Для правил остановки контроля «из последних r объектов будет k дефектных» при k≥2, r≥k, выпишем все состояния, которые приводят к наступлению остановки. Это будут следующие состояния:
,
,
,…,
,
,…, 
,…,
,…,
.
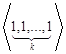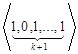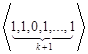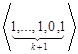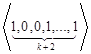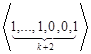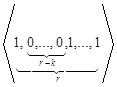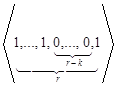Нетрудно видеть, что длину (количество позиций в состоянии), равную k, имеют всего 
состояний (т.е. всего одно состояние), длину, равную (k+1), имеют 
состояний. Рассуждая и далее так, получим, что длину, равную r, имеют 
состояний. Следовательно, вероятность события Е1, которое состоит в том, что наступит остановка по правилу «из последних r объектов будет k дефектных», равна:
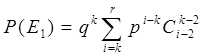или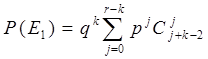 
.
Далее обозначим l – максимальную длину состояний, соответствующих событию Е1, l будет равна r. Заметим, что с0=1 и найдем ch – вероятности перехода из состояний, соответствующих событию Е1, в эти же состояния (h изменяется от 1 до l-1).
Будем рассуждать следующим образом. За h шагов может быть i дефектных объектов (i изменяется от 1 до k-1). При этом число шагов h не должно быть меньше числа дефектных объектов, но не должно превосходить числа равного (l-k+i). При этом число вариантов перехода из состояний, соответствующих событию Е1, в эти же состояния равно 
. Следовательно,
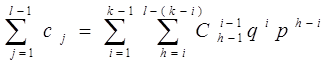
или
.
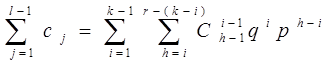Тогда:
.
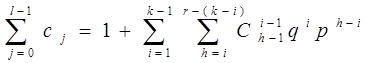Для математического ожидания числа проконтролированных объектов до остановки контроля по правилу «из последних r объектов будет k дефектных объектов» при k≥2, r≥k, когда вероятность каждого объекта быть годным равна р и быть дефектным равна q=1-p, согласно формуле (1) получаем выражение:
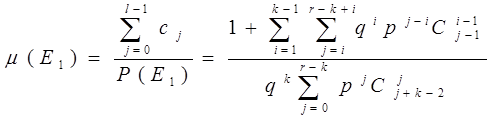. (2)
Фактически была доказана следующая теорема.
Теорема 1. Математическое ожидание числа проконтролированных объектов до остановки контроля при классическом контроле по правилу «из последних r объектов k дефектных объектов» при q – вероятности дефектности каждого объекта и p=1-q – вероятности годности каждого объекта равно (2).
Теперь рассмотрим случай контроля с памятью, т.е. случай, когда информация о последнем проконтролированном объекте при наступлении остановки контроля запоминается. Формально будем считать, что до начала контроля наблюдался дефектный объект. Для правил остановки контроля «из последних r объектов будет k дефектных» при k≥2, r≥k, выпишем все состояния (серии), которые приводят к наступлению остановки. Это будут следующие состояния:
,
,
,…,
,
,…, 
,…,
,…,
;
,
,
,…, 
,
,…, 
,…, 
,…,
.
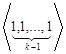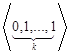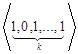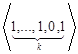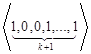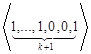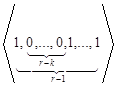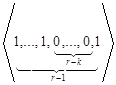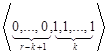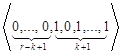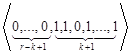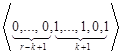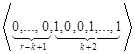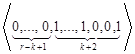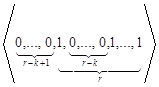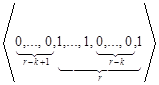Нетрудно видеть, что длину, равную k-1, и длину, равную (r-k+1)+(k), имеют 
состояний, длину, равную k, и длину, равную (r-k+1)+(k+1), имеют 
состояний. Рассуждая и далее так, получим, что длину, равную r-1, и длину, равную (r-k+1)+(r), имеют 
состояний. Следовательно, вероятность события 
, которое состоит в том, что наступит остановка по правилу «из последних r объектов будет k дефектных» при контроле с памятью, равна:
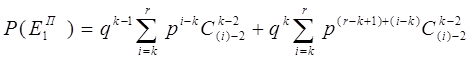
или
.
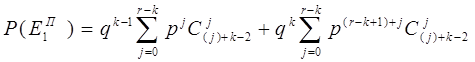Далее введем lП – максимальную длину состояний, соответствующих событию 
, lП будет равна 2r-k+1. Заметим, что с0=1 и найдем ch – вероятности перехода из состояний, соответствующих событию , в эти же состояния (h изменяется от 1 до lП-1). Рассуждать будем аналогично предыдущему случаю. В целях наглядности для количества шагов контроля, изменяющихся от 1 до r-1, и количества шагов контроля от r+1 до 2r-k+1 , представим структуру шагов в виде схем:
,
,
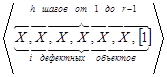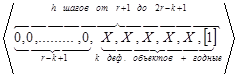где «1» – дефектный объект, «0» – годный объект, «Х» – либо дефектный, либо годный объект. Тогда:
.
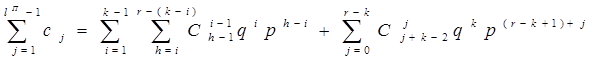Следовательно,
.
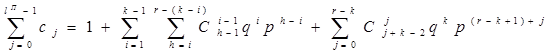Подставляя в формулу (1) найденные значения для вероятности наступления события и суммы вероятностей перехода из состояний, соответствующих этому событию в эти же состояния, получаем:
. (3)
Теперь сформулируем доказанное утверждение в виде теоремы.
Теорема 2. Математическое ожидание числа проконтролированных объектов до остановки контроля при контроле с памятью по правилу «из последних r объектов k дефектных объектов» при q – вероятности дефектности каждого объекта и p=1-q – вероятности годности каждого объекта равно (3).
Очевидно, что для любого фиксированного набора 
, 
и 
справедливо неравенство:
. (4)
Заключение
Правила остановки контроля для плана непрерывного контроля, в который они входят, играют существенную роль. На практике, применяя какие-либо правила остановки контроля, поступают следующим образом. Если реально проконтролированное число объектов до остановки контроля меньше математического ожидания числа проконтролированных объектов для фиксированного 
(вероятности годности объекта, т.е. для нормального хода производства объектов), то принимаются какие-либо меры для восстановления нормального хода производства. Это может быть замена или переналадка производственного оборудования в условиях поточного производства объектов или проведение профилактических мер при контроле показателей здоровья населения. Если же реально проконтролированное число объектов до остановки контроля равно или больше математического ожидания числа проконтролированных объектов для фиксированного , то контроль продолжается без принятия каких-либо мер. Интерпретировать это можно так: случилось то, что должно было случиться. В этом случае для классического контроля статистическая информация о контроле «обнуляется», а при контроле с памятью запоминается последний шаг контроля. Это обстоятельство является отличительным признаком контроля с памятью от классического контроля.
Рецензенты:
Пенский Олег Геннадьевич, доктор технических наук, доцент, профессор кафедры процессов управления и компьютерной безопасности, Пермский государственный национальный исследовательский университет, г. Пермь.
Ясницкий Леонид Нахимович, доктор технических наук, профессор, заведующий кафедрой прикладной информатики, Пермский государственный гуманитарно-педагогический университет, г. Пермь.
Библиографическая ссылка
Гусев А.Л. ПРАВИЛА ОСТАНОВКИ ДЛЯ КЛАССИЧЕСКОГО КОНТРОЛЯ И КОНТРОЛЯ С ПАМЯТЬЮ // Современные проблемы науки и образования. – 2013. – № 3. ;URL: https://science-education.ru/ru/article/view?id=9556 (дата обращения: 16.04.2024).