В условиях модернизации высшей школы актуальными являются проблемы повышения качества образования и оценивания качества обучения в вузах [7-8; 10]. В связи с этим для оценки статистических данных педагогических измерений и учебных достижений студентов в последнее время стал активно использоваться статистический анализ [1-5; 9], позволяющий методами математической статистики с помощью проверки статистических гипотез выявлять вероятностные закономерности.
В данной работе на примере результатов оценивания знаний студентов-заочников рассмотрены особенности проведения статистического анализа, связанные с использованием балльной шкалы измерения (оценивания) и частично затронутые в [1-4].
Хотя согласно теории измерительных шкал некорректно использовать среднее арифметическое в порядковой шкале, к которой относится балльная шкала, однако полностью игнорировать средние арифметические нецелесообразно из-за их привычности и распространенности. Поэтому представляется рациональным использовать одновременно оба метода - и метод средних арифметических рангов (баллов), и метод медианных рангов. Поэтому в данной работе проводится сопоставление результатов исследования параметрическими и непараметрическими (ранговыми) критериями. Статистический анализ проводился в системе Statistica [6].
На примере результатов сдачи тест-экзамена по высшей математике в четвертом семестре 116 студентами-заочниками, получившими допуск к экзамену по результатам выполнения индивидуальных домашних заданий (ИДЗ), в составе 10 групп (уровни фактора Группа), разбитых по 3 потокам (уровни ПБ, ПА1 и ПА2 фактора ПОТОК), проведен статистический анализ оценивания знаний в 3-мерном пространстве переменных: идз – набранные баллы за 4 ИДЗ (из 60 баллов – max), экз – набранные экзаменационные баллы (из 40 баллов – max), dt – разность моментов окончания и начала экзамена (в минутах).
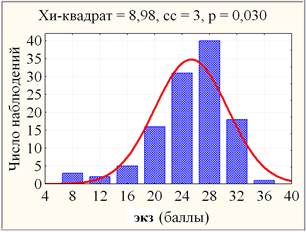
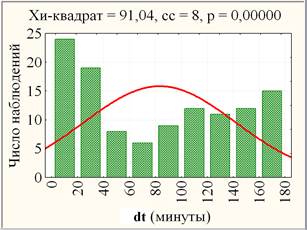
Для корректного применения параметрического дисперсионного анализа необходимо оценить сходство наблюдаемых распределений (гистограмм) переменных и уровней рассматриваемого фактора (ПОТОК, Группа) с теоретическим распределением по нормальному закону. Наиболее близким к нормальному является распределение переменной экз, но даже в этом случае критерий хи-квадрат показывает статистически значимое отличие (0,005 < р ≈ 0,03 < 0,05) для 8 интервалов группирования выборки объёма n = 116 согласно формуле Стэрджеса (рис. 1, слева). В случае dt (рис. 1, справа) отличие является высоко значимым ( р ≈ 0,00000 < 0,0005).
|
|
|
Рис. 1. Гистограммы экз и dt с соответствующими кривыми нормального распределения
Статистический анализ начнем с проверки переменных dt, экз и идз на корреляционную зависимость. Матрицы коэффициентов парных корреляций переменных приведены в табл. 1 (Пирсона r – в право-верхнем треугольнике над диагональю и Спирмена R – в лево-нижнем треугольнике под диагональю). В круглых скобках указаны соответствующие уровни значимости отличия коэффициентов корреляции от ноля. Согласно табл. 1, корреляцию между dt и экз , а также между идз и экз можно считать незначимой (0,100 < р), то есть экзаменационный результат не зависит значимо ни от времени dt, затраченного на выполнение экзаменационной работы, ни от качества допуска к экзамену по идз (в диапазоне от 33 до 60 баллов). Корреляцию между идз и dt (r ≈ R ≈ 0,274) можно считать сильно значимо (0,0005 < р ≈ 0,003 < 0,005) отличающуюся от ноля, тем не менее весьма далекой от единицы. При этом коэффициенты парных корреляций Пирсона r отличаются от соответствующих ранговых корреляций Спирмена R (например, r ≈ 0,122 и R ≈ 0,135 или r ≈ 0,134 и R ≈ 0,152) незначимо.
Таблица 1. Матрица коэффициентов парных корреляций Пирсона r и ранговых корреляций Спирмена R переменных dt, экз и идз
|
|
dt |
экз |
идз |
|
|
dt |
|
0,122 (p ≈ 0,192) |
0,2738 (p ≈ 0,003) |
r |
|
экз |
0,135 (p ≈ 0,148) |
|
0,134 (p ≈ 0,152) |
|
|
идз |
0,2742 (p ≈ 0,003) |
0,152 (p ≈ 0,103) |
|
|
|
|
R |
|
||
Таким образом, коэффициент парных корреляций демонстрирует устойчивость (табл. 1) к отклонению от нормальности распределений рассматриваемых переменных (рис. 1).
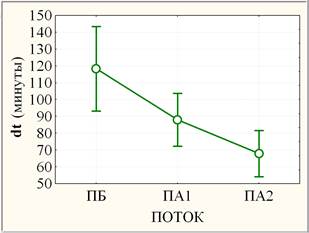
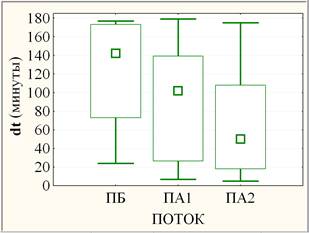
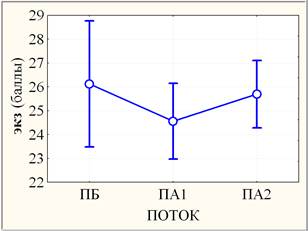
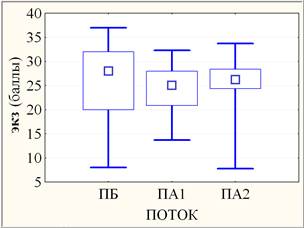
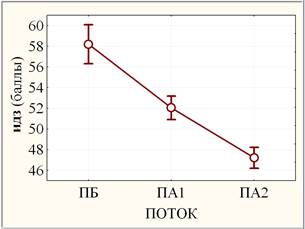
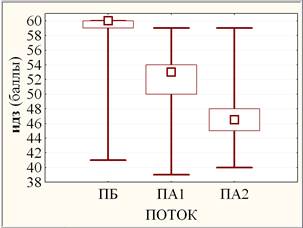
Значимость неоднородности переменных dt, экз и идз по потокам (рис. 2) оценивалась на основании однофакторного дисперсионного анализа.
|
|
|
|
|
|
|
|
|
Рис. 2. Слева: средние потоков (круги) с ±95% доверительными интервалами (усы); справа: медианы потоков (квадраты) с квартилями (прямоугольники) и размахами (усы)
Применение F-критерия параметрического дисперсионного анализа предполагает нормальное распределение внутри сравниваемых групп и однородность дисперсий в группах. Но F-критерий устойчив к отклонению от нормальности и однородности дисперсий [6]. В связи с нарушением в разной степени условия нормальности распределения выборок (рис. 1) далее применялся также и непараметрический критерий Краскела-Уоллиса, основанный на рангах, а не на исходных наблюдениях. В случае уровней ПБ, ПА1 и ПА2 фактора ПОТОК оба критерия единодушны в оценке сильно значимых (0,0005 < р < 0,005) различий результатов dt (на уровне значимости рF ≈ 0,0019 и рКУ ≈ 0,0022 соответственно), незначимых (р > 0,10) различий результатов экз и высоко значимых (р < 0,0005) различий результатов идз по совокупности ПБ, ПА1 и ПА2. При парном сравнении ПБ, ПА1 и ПА2 оба критерия также единодушны в оценке незначимых (р > 0,10) различий результатов экз и высоко значимых (р < 0,0005) различий результатов идз, но различаются в случае dt: если критерий Краскела-Уоллиса оценивает выборки ПА1 и ПБ или ПА1 и ПА2 как попарно однородные (р > 0,10), то в рамках параметрического дисперсионного анализа апостериорный критерий наименьшей значимой разности (НЗР) оценивает различие между ПА1 и ПБ как слабо значимое (0,050 < р ≈ 0,075 < 0,100), а различие между ПА1 и ПА2 как статистически значимое (0,005 < р ≈ 0,027 < 0,050). При парном сравнении ПБ и ПА2 в случае dt критерий НЗР дает сильно значимое (0,0005 < р < 0,0050) различие на уровне значимости р ≈ 0,0008, а критерий Краскела-Уоллиса – сильно значимое (0,0005 < р < 0,0050) различие на уровне значимости р ≈ 0,0026, что также подтверждается парным ранговым критерием Манна-Уитни на уровне значимости р ≈ 0,0013. Таким образом, сильно значимая неоднородность результатов dt по совокупности ПБ, ПА1 и ПА2 согласно непараметрическому критерию Краскела-Уоллиса складывается из сильно значимой неоднородности ПБ и ПА2 при попарной однородности ПА1 и ПБ или ПА1 и ПА2 в отличие от менее корректного параметрического дисперсионного анализа, в рамках которого усматривается неоднородность разного уровня значимости во всех парах потоков ПБ, ПА1 и ПА2.
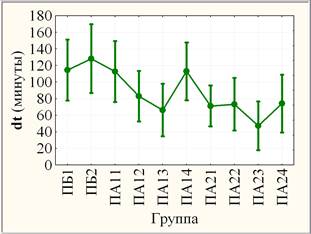
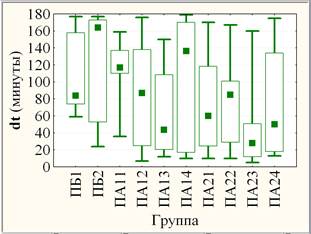
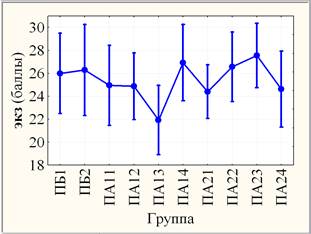
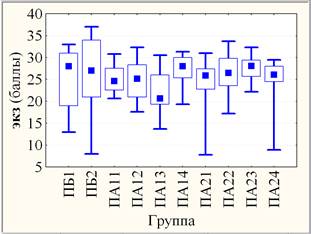
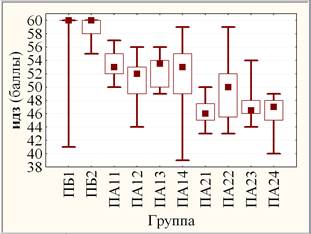
С учетом составной структуры потоков ПБ (2 группы), ПА1 (4 группы) и ПА2 (4 группы) аналогично оценена значимость неоднородности переменных dt, экз и идз по группам (рис. 3). Оба критерия единодушны в оценке незначимых различий результатов экз и высоко значимых различий результатов идз по совокупности групп, а различия результатов dt (на уровне значимости рF ≈ 0,017 и рКУ ≈ 0,024) оцениваются как статистически значимые. В последнем случае увеличение уровня значимости различий результатов dt по совокупности групп в сравнении с совокупностью потоков объясняется прежде всего уменьшением объема выборки (группы в сравнении с потоком) и, как следствие, увеличением 95% доверительного интервала.
|
|
|
|
|
|
|
|
|
Рис. 3. Слева: групповые средние (круги) с ±95% доверительными интервалами (усы); справа: групповые медианы (квадраты) с квартилями (прямоугольники) и размахами (усы)
При парном сравнении групп возникает широкий спектр оценок уровней значимости по любой переменной. Даже в случае незначимых различий результатов экз (по совокупности групп) на примере группы ПА13 критерии НЗР и Краскела-Уоллиса дают статистически значимое (0,005 < р < 0,050) отличие от ПА14 (рНЗР ≈ 0,029 и рКУ ≈ 0,035), ПА22 (рНЗР ≈ 0,034 и рКУ ≈ 0,043), ПА23 (рНЗР ≈ 0,008 и рКУ ≈ 0,005) и незначимое (р > 0,10) от ПА11, ПА12, ПА21, ПА24; при этом парное отличие ПА13 от ПБ1 (рНЗР ≈ 0,084 и рКУ ≈ 0,177), ПБ2 (рНЗР ≈ 0,086 и рКУ ≈ 0,108) является слабо значимым (0,05 < р < 0,10) по критерию НЗР и незначимым (р > 0,10) по критерию Краскела-Уоллиса.
Выводы
1. На основании критерия хи-квадрат выявлено значимое отличие распределений рассматриваемых переменных от нормального закона: от статистически значимого (0,005 < р < 0,05) для экз и до высоко значимого (р < 0,0005) для dt.
2. Корреляция между dt и экз , а также между идз и экз оценена как незначимая, то есть экзаменационный результат не зависит значимо ни от времени dt, затраченного на выполнение экзаменационной работы, ни от качества допуска к экзамену по идз. Корреляция между идз и dt (r ≈ R ≈ 0,274) сильно значимо отличается от ноля, тем не менее весьма далека от единицы. При этом коэффициенты парных корреляций Пирсона r отличаются от соответствующих ранговых корреляций Спирмена R незначимо.
3. На основании однофакторного параметрического и непараметрического дисперсионных анализов оценена значимость неоднородности переменных dt, экз и идз по потокам: сильно значимая (0,0005 < р < 0,005) для dt, незначимая (р > 0,10) для экз и высоко значимая (р < 0,0005) для идз по совокупности 3 потоков. При парном сравнении потоков оба критерия также единодушны в оценке незначимых различий результатов экз и высоко значимых различий результатов идз, но различаются в случае dt: согласно непараметрическому критерию Краскела-Уоллиса сильно значима неоднородность ПБ и ПА2 при попарной однородности ПА1 и ПБ или ПА1 и ПА2 в отличие от параметрического дисперсионного анализа, в рамках которого усматривается неоднородность разного уровня значимости во всех парах потоков ПБ, ПА1 и ПА2.
4. Аналогично оценена значимость неоднородности переменных dt, экз и идз по 10 группам: оба критерия единодушны в оценке незначимых (р > 0,10) различий результатов экз и высоко значимых (р < 0,0005) различий результатов идз по совокупности групп, а различия результатов dt по совокупности групп оцениваются как статистически значимые (0,005 < р < 0,050). При парном сравнении групп оба критерия единодушно дают широкий спектр оценок уровней значимости по любой переменной, в том числе и по экз.
Работа выполнена в рамках государственного задания «Наука≈ № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России≈ по контрактам П691.
Рецензенты:
Трифонов Андрей Юрьевич, д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Арефьев Константин Петрович, д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Михальчук А.А., Арефьев В.П., Филипенко Н.М. СРАВНИТЕЛЬНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ ПАРАМЕТРИЧЕСКИХ И НЕ-ПАРАМЕТРИЧЕСКИХ МЕТОДОВ ОЦЕНИВАНИЯ ЗНАНИЙ В СИСТЕМЕ ЗАОЧНОГО ОБУЧЕНИЯ // Современные проблемы науки и образования. 2013. № 3. ;URL: https://science-education.ru/ru/article/view?id=9553 (дата обращения: 22.02.2026).