Введение
Прогресс в области телекоммуникаций влечет за собой расширение инфраструктуры и все более широкий охват отдаленных и малонаселенных регионов, где, в силу объективных причин, предпочтение все чаще отдается беспроводным сетям.
В настоящей работе мы рассматриваем метод поиска оптимального способа развития беспроводной сети (мест новых точек доступа или базовых станций), основанный на критериях охвата (покрытия) надежным доступом важных территорий и минимальной стоимости оборудования. Проблема поиска оптимального расположения и подбора типов элементов оборудования растущей сети сформулирована как многокритериальная дискретная задача оптимизации с ограничениями. Проблема моделирования радиопоглощающих свойств среды распространения также сформулирована и решена как дискретная задача оптимизации.
Рассматриваемая проблема оптимального размещения точек доступа – предмет дискуссий инженеров и сетевых администраторов на интернет-форумах и в научных публикациях. Предлагается как готовое к использованию программное обеспечение, которое в состоянии предсказывать распространение сигнала в соответствии с физическими свойствами элементов окружающей среды, так и различные методы поиска нового размещения точек доступа с оптимальным распространением сигнала [6] или размещение, которое предусматривает лучшую локализацию мобильного положения оборудования WLAN (вычисление его координат) в области вещания сети [4]. Прогноз уровня сигнала в каждом пункте, учитывающем потери трассы от стен, потолков и других элементов, является известной технической проблемой [9].
Современная литература по данной проблематике предлагает много способов постановки и решения аналитическим путем задачи предсказания уровня распространяемого сигнала (в уличных условиях и внутри зданий) и различные детерминированные и стохастические методы оптимизации для нахождения оптимального размещения.
Используя эмпирическую внутреннюю модель распространения волны Мотли-Кинана с учетом типа стен и потолков для вычисления потери трассы, работа [10] представляет технику размещения точек доступа для оптимального внутреннего покрытия сигналом. Генетический алгоритм используется для нахождения конфигурации с меньшим значением максимальной потери пути для каждой точки пространства. В [7] авторы также предлагают строго типизированное генетическое программирование, чтобы решить проблему конфигурации точек доступа с их оптимальным расположением, предоставляющих лучшее покрытие.
Большинство вышеупомянутых работ основано на модели распространения сигнала, которая рассматривает логарифмическую потерю от каждого препятствия (стены, потолки) по некоторым информационным таблицам, но часто мы не знаем даже точного строительного материала наших элементов среды и их точной геометрии, и реальное поглощение может отличаться очень существенно.
В нашем случае оптимальное покрытие - одна из целей. Второй важный критерий - минимальная стоимость беспроводного оборудования и его установки. В случае если стоимость размещаемого оборудования не зависит от места его размещения, оптимизация по второму критерию сводится к минимизации количества размещаемых точек доступа. Результаты вышеупомянутых методов трудно интерпретировать, если оптимальное место для точки доступа расположено далеко от электрической проводки, стен или других конструктивных элементов, где мы в состоянии закрепить и запитать оборудование, вследствие чего данную задачу следует считать задачей размещения с запрещенными областями.
Для задачи размещения (иначе — множественная задача Вебера) с запрещенными зонами, барьерами и неевклидовой функцией расстояния рассмотрены лишь некоторые частные случаи [5]. В [1] рассмотрен метод приближенного решения таких задач, основанный на идеях метода изменяющихся вероятностей [2]. В настоящей работе мы показываем практическую применимость данного метода к сформулированной задаче оптимального размещения точек доступа беспроводной сети.
Исходная информация и методы
Минимальная информация о геометрии окружающей среды (расположение стен, деревьев и других объектов) всегда доступна из карт, схем или непосредственного визуального наблюдения. Радиопоглощающие свойства элементов окружающей среды доступны из информационных таблиц [7] и в состоянии быть определенными более точно, если элемент расположен между существующим передатчиком и приемником или в зоне Френеля между ними. В сложных случаях поглощающие свойства могут быть определены как решение вложенной задачи оптимизации.
Кроме того, у нас есть информация о возможности и приблизительной стоимости размещения новой точки доступа в каждом месте. Так, места, где у нас есть электрическая проводка (по крайней мере, места с существующими аппаратными средствами беспроводного клиента), лучше подходят для установки новых точек доступа, чем отдаленные от инфраструктуры электропитания и зданий. Кроме того, лицо, принимающее решения, в состоянии определить некоторое число возможных мест новых точек доступа в соответствии с причинами, которые очевидны для него, но трудно формализуемы.
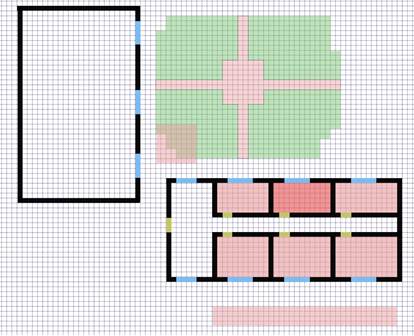
Рис. 1. Фрагмент схемы с требуемыми зонами покрытия и элементами окружения
Чтобы упростить наши вычисления, разделим нашу область на ячейки. Как правило, реальные задачи не позволяют нам игнорировать вертикальные позиционные соотношения элементов окружающей среды и инфраструктуры. Именно поэтому мы должны рассматривать нашу среду как 3D-пространство. Для простоты описания и представления на бумаге мы рассматриваем 2-мерный случай.
Допустим, что оборудование расположено в центрах клеток, а границы элементов окружающей среды (препятствия, такие как стены, окна, деревья и т.д.) совпадают с границами любого набора клеток. Так, мы рисуем схему нашей среды с существующими и новыми точками доступа и препятствиями и существующие и перспективные зоны вещания нашей сети, как будто мы отмечаем элементы в тетради в клетку (рис. 1). Стены отмечены черным цветом, окна и двери – голубым и желтым, зеленые насаждения соответственно зеленым. Розовым отмечены желательные зоны покрытия, а красным – зона с более высоким приоритетом.
Пусть в нашей схеме есть несколько зон уверенного приема. Мы определяем весовой коэффициент для каждой из этих областей (приоритет). Кроме того, возможно установить некоторый минимальный битрейт для той или иной области. Таким образом, у нас есть Nc ячеек, которым мы должны сопоставить весовые коэффициенты vj и минимальные битрейты bj, 1 ≤ j ≤ Nc.
Пусть есть Np точек (клеток), где мы в состоянии поместить точки доступа. Для каждой из этих клеток мы рассматриваем Nt типов аппаратных средств (различные антенны, усилители и т.д.). Для каждого из этих мест мы знаем также приблизительную стоимость вспомогательного оборудования (такого, как провода электропитания или автономное электропитание, кронштейны антенны и т.д.) Ci, 1≤i≤Np, и стоимость каждого вида аппаратных средств Ck также известна, 1≤k≤Nc.
Определим матрицу X булевых переменных xik. Полагаем, что значение переменной xik, равное 1, означает, что мы решили поместить аппаратные средства точки доступа k-го типа в i-й возможной клетке, а установка значения xik=0 означает, что мы решили поместить туда другой вид оборудования или не поместить никакой точки доступа в i-й клетке.
Наша цель состоит в том, чтобы поставлять максимальный битрейт в максимальном количестве клеток в соответствии с их коэффициентами веса при минимальных затратах.
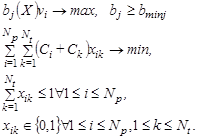
Здесь bj (X) - максимальный возможный битрейт в j-й точке приема (хотя все беспроводные устройства – дуплексные, для простоты описания мы называем точки доступа передающими, а клиентские устройства - принимающими). Точки доступа установлены в соответствии с вектором X логических переменных, vj - коэффициент веса j-й получающей точки, Np - общее количество возможных мест для точек доступа в будущей системе, Nt - число типов оборудования точки доступа (точки доступа или беспроводные маршрутизаторы, оборудованные соответствующими типами антенн), bmin j - минимальные гарантируемые битрейты, необходимые для некоторых точек приема.
Определим поглощающие свойства каждого препятствия, показанного в нашей схеме. Пусть Пl - поглощение (в децибелах) сигнала, проходящего через слой l-го препятствия в слое ячеек. Начальные значения могут быть получены из информационных таблиц [7]. Например, для стены Пl = -7 дБ, для окна -2 дБ, для растущих деревьев -3 дБ на каждый метр (значение для ячейки зависит от ее размера). Ниже мы рассматриваем метод, разрешающий нам определить более точно значение Пl в соответствии с экспериментальными данными.
Далее уровень сигнала (рис. 2) i-й точки доступа, которую мы можем получить в j-й клетке, может быть вычислен как
![]() .
.
Здесь Prij(X) - уровень сигнала (дБ) i-й точки доступа, полученной в j-й принимающей точке, Gti - усиление антенны точки доступа (включая потерю всех кабелей), Gr – усиление антенны пункта получения (также включая все кабели), Lij (SOBST) является потерей пути между i-й точкой доступа и j-й получающей точкой с конфигурацией препятствий (стены, окна, деревья и т.д.), описанной множеством SOBST. Dij - расстояние (в метрах) между i-й точкой доступа и j-й получающей точкой.
Битрейт, который обеспечивается для этого уровня сигнала,
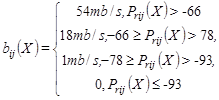
Здесь, bij (X) - максимальный доступный битрейт связи между i-й точкой доступа и j-й получающей точкой. Уровни сигнала выражены в дБ.
Учитывая несколько возможных вариантов беспроводного оборудования для каждой точки доступа, уровень сигнала равен
![]() .
.
Чтобы вычислить уровень сигнала, принимаемого в некоторой ячейке от некоторой точки доступа, мы должны определить, какие препятствия лежат между точкой доступа и покрытой ячейкой, учитывая зону Френеля. Методика оценки зоны Френеля в использованной нами дискретной системе координат и затухания сигнала при прохождении через зону Френеля приведена в [8].
Таким образом, уровень сигнала, принимаемого в j-й точке, равен
![]()
Здесь Lij - полная потеря трассы, вызванная препятствиями, расположенными между i-й точкой доступа и j-й ячейкой приема. Nij – расстояние между точками, выраженное числом ячеек координатной системы между ними, dcell – размер ячейки. Таким образом, уровень сигнала от i-й точки доступа, оборудованной аппаратными средствами k-го типа, принимаемого в j-й клетке. Радиооборудование клиента, расположенное в каждой из покрытых клеток, в состоянии установить связь с любой точкой доступа, но оно выбирает точку доступа с максимальным уровнем сигнала. Уровень сигнала «лучшей» точки доступа, полученной в j-й клетке, может быть вычислен как
![]() .
.
Для точек, в которых требуется обеспечить приемлемый уровень сигнала, введем дополнительную функцию, учитывающую корректирующую штрафную составляющую при недостаточном уровне сигнала.
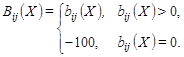
Таким образом, первый критерий преобразуется в следующую целевую функцию:
![]()
Таким образом, у нас есть дискретная задача оптимизации с псевдобулевыми функциями с ограничениями, имеющая 2 критерия. Для решения задач этого вида накоплен большой опыт применения алгоритма на базе метода изменяющихся вероятностей, предложенного в [2] в его версии, описанной в [1; 3]. С целью сокращения 2-го критерия и получения Парето-оптимального набора решений мы преобразуем критерий в ограничение количества размещаемых точек. Заключительный шаг алгоритма - сравнение Парето-оптимальных решений, показанных вместе со значениями возможных битрейтов каждой ячейки для различных значений стоимости достижения такого охвата устойчивой связью.
Результаты
Мы рассмотрели задачу выбора места для дополнительных точек доступа растущей сети и их типов как задачу оптимизации, которая основана на адаптации модели окружающей среды распространения радиоволн. Хотя наша модель учитывает только наиболее важную информацию о взаимодействии сигнала и окружающей среды (фактически только поглощение и шум без определения его характера), эта модель позволяет нам предсказывать уровень сигнала и битрейт каждой перспективной области, по крайней мере, как грубую оценку. В основном наш метод совпадает с обычной практикой инженерных вычислений, но позволяет собирать всю информацию о нашей среде в единую модель и находить одно или более Парето-оптимальных решений, принимающих во внимание всю доступную информацию об окружающей среде и стоимости размещения нового оборудования.

Рис. 2. Ход решения и результаты
На рисунке 2 изображены ход решения задачи и результаты, полученные при различных ограничивающих условиях. По условиям задачи, точки доступа могут располагаться в пределах двух строений, остальные области составляют запрещенную зону задачи. Части 1 и 2 отражают матрицу вероятностей применяемого метода изменяющихся вероятностей [1] после первого и четвертого шагов алгоритма соответственно. Результаты алгоритма для двух и четырех размещаемых точек доступа изображены на частях 4 и 5. В красных и желтых зонах покрытие достаточно для уверенной работы оборудования, зоны с недостаточным уровнем сигнала обозначены темно-синим. Такой подход позволяет специалисту, занимающемуся размещением оборудования, получить более широкий спектр вариантов, различающихся зонами охвата и стоимостью (количеством) размещаемого оборудования, и принять более продуманное решение. Для сравнения на части 3 приведен результат полного перебора для двух точек доступа.
Результаты нашего метода могут легко интерпретироваться специалистом, так как возможные места точек доступа определены в первом шаге. Практика показывает необходимость проверить реальный уровень сигнала после первоначального решения задачи предлагаемым методом и повторить метод с новыми значениями измерений. Для системы, подобной показанной на рис. 1, различие между реальными и расчетными ценностями сигнала составляет до 12 дБ, второй шаг дает максимальную ошибку не более 6 дБ, что приемлемо для инженерных вычислений.
Заключение
Алгоритм, использующий метод изменяющихся вероятностей и предложенную модель, позволяет решить задачу оптимального размещения на основе приблизительной пространственной схемы радиопоглощающей среды.
Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.B37.21.0625
Рецензенты:
Антамошкин А.Н., д.т.н., профессор, зав. кафедрой математического моделирования и информатики ФГОУ ВПО «Красноярский государственный аграрный университет», г. Красноярск.
Петров М.Н., д.т.н., профессор, зав. кафедрой электронной техники и телекоммуникаций Сибирского государственного аэрокосмического университета им. академика М.Ф. Решетнева, г. Красноярск.
Библиографическая ссылка
Казаковцев Л.А., Гудыма М.Н., Ступина А.А., Кириллов Ю.И. ЗАДАЧА ВЫБОРА ОПТИМАЛЬНОГО РАЗМЕЩЕНИЯ ЭЛЕМЕНТОВ БЕСПРОВОДНОЙ СЕТИ // Современные проблемы науки и образования. 2013. № 3. ;URL: https://science-education.ru/ru/article/view?id=9551 (дата обращения: 22.02.2026).



