Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дивеев А.И. 1 Шмалько Е. Ю. 1

---

1 Федеральное государственное бюджетное учреждение науки Вычислительный центр им. А. А. Дородницына Российской академии наук

Рассматривается задача синтеза управления, которая состоит в нахождении многомерной функции управления от координат пространства состояний. Проблема, связанная с нахождением математических выражений, относится к задачам символьной регрессии. В настоящее время появилась возможность выполнять символьную регрессию с помощью вычислительной машины. В работе для автоматизации поиска функции управления предлагается использовать метод символьной регрессии на базе сетевого оператора. Сетевой оператор является особой структурой данных, позволяющей представить любое математическое выражение в виде матрицы, содержащей номера унарных и бинарных операций. Изменяя по определенным правилам значения элементов матрицы сетевого оператора, метод позволяет получать новые математические выражения. Такое представление обеспечивает возможность применения различных поисковых алгоритмов для нахождения оптимального математического выражения. В работе применяется метод интеллектуальной эволюции. Представлен численный пример синтеза управления движением мобильного робота по траектории с фазовыми ограничениями.

Статья в формате PDF

229 KB

мобильный робот

генетический алгоритм

сетевой оператор

синтез управления

символьная регрессия

1. Дивеев А. И. Численный метод сетевого оператора для синтеза системы управления с неопределенными начальными значениями // Известия РАН. Теория и системы управления. – 2012. – № 2. – С. 63-78

2. Дивеев А. И., Софронова Е. А. Метод сетевого оператора и его применение в задачах управления. – М.: РУДН, 2012. – 182 с.

3. Дивеев А. И., Шмалько Е. Ю. Синтез системы управления посадкой на Марс // Труды ИСА РАН. Динамика неоднородных систем / Под ред. чл.-корр. РАН Ю. С. Попкова. – М.: ИСА РАН, Книжный дом ЛИБРОКОМ, 2010. – Вып. 14. – Т. 53(1). – С. 275–281.

4. Дивеев А. И., Шмалько Е. Ю. Применение методов интеллектуальной эволюции для синтеза систем управления // Интеллектуальные системы: Труды Десятого международного симпозиума / Под ред. К. А. Пупкова. – М.: РУСАКИ, 2012. – С.54-58.

5. Дивеев А. И., Шмалько Е. Ю. Метод интеллектуальной эволюции для синтеза систем управления. Программа для ЭВМ № 2012661004.

6. Мартыненко Ю. Г. Управление движением мобильных колесных роботов // Фундаментальная и прикладная математика. – 2005. – Т. 11, № 8. – С. 29-80.

7. Dubins L. E. On curves of minimal length with a constraint on average curvature and with prescribed initial and terminal positions and tangents // Amer. J. Math. – 1957. – Vol. 79. – P. 497-516.

8. Koza J. R. Genetic Programming: On the Programming of Computers by Means of Natural Selection. – Cambridge, Massachusetts, London, MA: MIT Press, 1992. – 819 p.

Введение

Символьная регрессия представляет собой процедуру написания математических выражений для выявления закономерностей по экспериментальным данным, идентификации моделей исследуемых систем и определения функциональных зависимостей в многофакторном анализе денных. В подавляющем большинстве случаев символьная регрессия выполняется исследователем вручную. Разработчик записывает математическое выражение с точностью до значений параметров. Вычислительный алгоритм использовался для поиска оптимальных значений параметров. После появления генетического программирования [8] стало возможным выполнять символьную регрессию с помощью вычислительной машины. Генетическое программирование использует эволюционный вычислительный алгоритм для поиска решений в форме строки символов. Строка символов при этом кодирует различные часто нечисловые структуры: электронные цепи, химические реакции, технические конструкции и др. К задачам символьной регрессии следует также отнести и задачу синтеза управления. В работе рассматривается метод машинной символьной регрессии на основе метода сетевого оператора [2] для решения задачи синтеза управления.

Постановка задачи

Рассмотрим постановку задачи синтеза управления [1,3].

Задана математическая модель объекта управления

, (1)

где – вектор состояния объекта управления, , , – вектор управления, , , , – ограниченное замкнутое множество.

Задано множество начальных значений

. (2)

Заданы терминальные условия или цель управления

, . (3)

Задан критерий качества управления в виде функционала

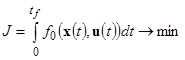, (4)

где – время управления, которое может быть не задано и определяться по условию (3) достижения цели управления.

Необходимо найти управление в виде многомерной функции от компонент вектора пространства состояний

. (5)

Функция должна обладать следующими свойствами. Функция должна удовлетворять ограничениям на управление

, . (6)

При подстановке функции в модель объекта управления (1) получаем систему дифференциальных уравнений . Полученная система уравнений для любого начального значения из заданной области (2) начальных значений имеет решение в форме векторной функции времени . Данное решение за конечное время достигает цели управления (3)

, , (7)

и обеспечивает минимум функционалу (4) качества управления на множестве всех допустимых управлений , удовлетворяющих ограничениям ,

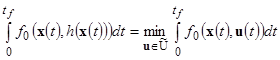. (8)

Поскольку при решении задачи синтеза необходимо найти вид многомерной функции, то данную задачу следует отнести к классу задач символьной регрессии. Машинные методы символьной регрессии появились с возникновением генетического программирования [8]. В настоящей работе рассматривается решение задачи синтеза управления на основе метода сетевого оператора [2], который относится также к методам символьной регрессии.

Метод сетевого оператора

Сетевой оператор предназначен для описания математических выражений, построенных на множествах переменных, параметров, унарных и бинарных операций.

Множество переменных

. (9)

Множество параметров

. (10)

Множество унарных операций

. (11)

Множество бинарных операций

. (12)

Сетевой оператор представляет собой ориентированный граф со следующими свойствами:

a) в графе отсутствуют циклы;

b) к любому узлу, который не является источником, имеется хотя бы один путь от источника;

c) от любого узла, который не является стоком, имеется хотя бы один путь до узла-стока;

d) каждому узлу-источнику соответствует элемент из множества переменных или параметров;

e) каждому узлу соответствует бинарная операция из множества бинарных операций ;

f) каждой дуге соответствует унарная операция из множества унарных операций .

Любой ориентированный граф с указанными свойствами соответствует какому-либо математическому выражению. Для перевода сетевого оператора в математическое выражение необходимо руководствоваться следующими правилами:

- вычисление унарной операции выполняем только для дуги, которая выходит из узла, не имеющего входящих дуг;

- удаляем дугу из графа после вычисления унарной операции;

- выполняем бинарную операцию в узле сразу после того, как выполнена унарная операция, приводящая в данный узел;

-заканчиваем вычисления, как только пройдены и удалены все дуги в графе.

Рассмотрим сетевой оператор, представленный на рис.1 с двумя узлами-источниками.

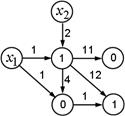
Рис.1. Пример сетевого оператора

Согласно правилам, сначала находим узел-источник, не имеющий входящих дуг. Примем за узел-источник . Далее выбираем исходящую их этого узла-источника дугу и вычисляем бинарную операцию, обозначенную в том узле, куда приводит выбранная дуга. Если бинарная операция для данного узла ранее не выполнялась, то первым аргументом для бинарной операции является единичный элемент данной операции. Вторым аргументом является результат унарной операции, приводящей в данный узел. Так на первой итерации результат бинарной операции равен результату унарной операции. Удаляем дуги и переходим к графу, представленному на рис. 2.

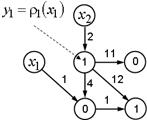
Рис. 2. Пример сетевого оператора после 1-ой итерации

Далее в соответствии с правилами a)-d) выполняем все последующие итерации. Если бинарная операция для данного узла выполняется не первый раз, то ее предыдущий результат присваивается одному из ее аргументов. Выполняем вычисления, пока имеется хотя бы одна дуга в графе.

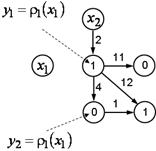
Рис. 3. Пример сетевого оператора после 2-ой итерации

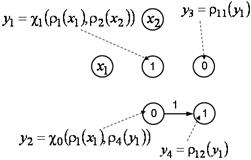
Рис. 4. Пример сетевого оператора перед последней итерацией

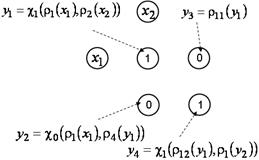
Рис. 5. Пример сетевого оператора после всех итераций

В результате получаем четыре математических выражения:

, , , .

Итоговый вид математических выражений зависит от элементов множеств унарных и бинарных операций. В работе [2] используют 24 унарных и 8 бинарных операций.

, , , , , , , , , , , , , , , , , , , , , , , ,

, , , , , , , .

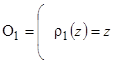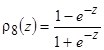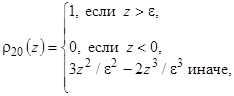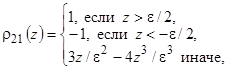Все бинарные операции являются коммутативными, ассоциативными и имеют следующие единичные элементы. Нумерация бинарных операций начинается с нуля, так чтобы номера наиболее часто используемых операций сложения и умножения совпадали с их единичными элементами.

Подставим элементы описанных множеств в полученные после вычислений по примеру сетевого оператора математические выражения, получаем

,

,

,

.

В памяти компьютера сетевой оператор представляется в виде матрицы сетевого оператора (NOM = Network Operator Matrix). Она формируется на основе матрицы смежности орграфа , , , где – количество узлов в графе.

Рассмотрим сетевой оператор, представленный на рис.1. Первоначально пронумеруем узлы графа, используя топологическую сортировку: номер узла, откуда выходит дуга, должен быть меньше номера узла, куда входит дуга. На рис. 6 приведен граф сетевого оператора с топологической нумерацией узлов.

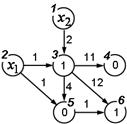
Рис. 6. Граф с топологической нумерацией

Граф, представленный на рис.10, имеет следующие матрицу смежности и матрицу сетевого оператора.

, .

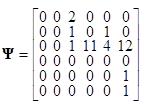Матрицы сетевого оператора не достаточно для написания математического выражения, так как она не хранит данных о переменных и параметрах. Эта информация содержится в начальных значениях вектора узлов , который в процессе вычисления используется для хранения промежуточных результатов.

Для получения математического выражения по матрице сетевого оператора необходимо пройти по каждому ряду последовательно . В каждом ряду мы рассматриваем элементы, следующие за диагональным элементом . Если встречается ненулевой элемент, то производим вычисления согласно уравнению

если. (13)

где , .

Для рассматриваемого примера имеем

,, , , , , , , ,, , , , , .

В результате получаем те же результаты, что и при вычислении по графу: , , , .

Синтез управления мобильным роботом

Математическая модель объекта управления имеет вид [4,6]

, (14)

, (15)

, (16)

где , − координаты положения центра масс объекта на плоскости, φ – угол между вектором скорости объекта и осью , , − компоненты вектора управления , регулирующие уровень напряжения на левом и правом двигателях колес робота.

Заданы ограничения на управление

, . (17)

В отличие от модели из [6,7] компоненты управления могут иметь отрицательные значения, обеспечивающие движение робота назад.

Задано терминальное состояние

. (18)

Задано множество начальных условий

(19)

Заданы функционалы, определяющие критерии качества управления

, (20)

, (21)

где индекс означает, что вычислено для начальных условий ,

,

– малая положительная величина; − заданное максимальное время процесса управления.

Задача синтеза заключается в нахождении функции управления. Необходимо синтезировать систему управления в виде

, (22)

, (23)

где − вектор параметров, который также ищем в процессе решения задачи.

Для решения рассматриваемой задачи синтеза (1)–(8) согласно методу сетевого оператора было сформировано базисное решение.

, (24)

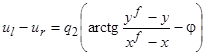, (25)

где .

При синтезе задано терминальное состояние и множество начальных условий

.

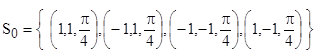Для получения решения был использован программной комплекс для синтеза систем управления методом интеллектуальной эволюции [4, 5].

В результате было получено следующее решение

, ,

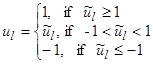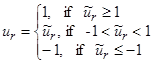где , , , .

Траектория движения объекта из четырех начальных положений, при которых осуществлялся синтез управления, представлена на рис.7.

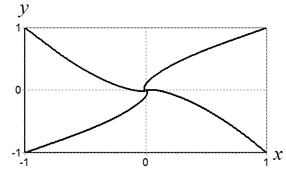
Рис. 7. Траектория движения объекта при синтезированном управлении

На рис. 8 представлено движение робота от точки к точке в обход заданных препятствий. Графики управлений приведены на рис. 9 и 10.

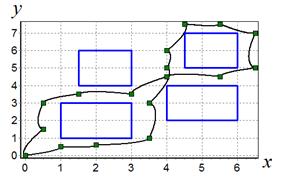
Рис. 8. Движение объекта по заданной траектории

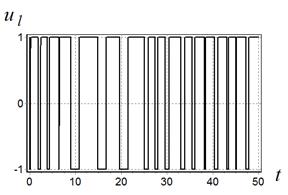
Рис. 9. Компонента управления при движении объекта по траектории

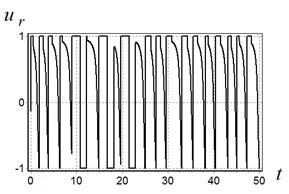
Рис. 10. Компонента управления при движении объекта по траектории

По результатам графиков видно, что нелинейная синтезированная система управления позволяет двигаться мобильному роботу практически точно по заданным точкам траектории. Характер пути вполне сохраняет форму траектории, но в каждой заданной точке при получении новой цели управления происходит коррекция направления движения.

Из сказанного следует вывод, что метод сетевого оператора позволяет синтезировать нелинейную систему управления, обеспечивающую качественное движение мобильного робота по траектории.

Работа выполнена по теме гранта РФФИ № 11-08-00532-а.

Рецензенты:

Дикусар Василий Васильевич, профессор, доктор физико-математических наук, главный научный сотрудник отдела прикладных проблем оптимизации Федерального государственного бюджетного учреждения науки Вычислительного центра им. А. А. Дородницына Российской академии наук, г. Москва.

Юрков Николай Кондратьевич, профессор, доктор технических наук, заведующий кафедрой конструирование и производство радиоаппаратуры Пензенского государственного университета, г. Пенза.

Библиографическая ссылка