Перед педагогической наукой и школой постоянно ставятся задачи совершенствования процесса обучения. При этом уделяется особое внимание вопросам, связанным с повышением уровня предметной (в частности математической) подготовки учащихся, формированием у них практических умений и навыков, развитием приемов мыслительной деятельности, а также развитием пространственного мышления (процесса создания, оперирования и преобразования пространственных образов).
Динамично развивающееся современное общество предъявляет новые требования к системе образования. Новые федеральные государственные образовательные стандарты, отвечая требованиям времени, не только смещают образовательный акцент на формирование у ученика личностных качеств, но и предлагают конкретные подходы, обеспечивающие этот переход. Примером одного из таких подходов является внедрение инновационных методов в обучение.
Инновация – это не всякое новшество или нововведение, а только такое, которое серьёзно повышает эффективность действующей системы. Инновационные методы включают в себя активные и интерактивные методы.
Целевыми ориентациями интерактивного обучения являются:
- активизация индивидуальных умственных процессов учащихся;
- возбуждение внутреннего диалога у учащегося;
- обеспечение понимания информации, являющейся предметом обмена;
- активизация индивидуальных умственных процессов учащихся;
- возбуждение внутреннего диалога у учащегося;
- обеспечение понимания информации, являющейся предметом обмена;
- индивидуализация педагогического взаимодействия;
- вывод учащегося на позицию субъекта обучения;
- достижение двусторонней связи при обмене информацией между учащимися.
При традиционном обучении учитель выполняет роль «фильтра», пропускающего через себя учебную информацию, при интерактивном обучении – помощника в работе, корректирующего направления потоков учебной информации.
Интерактивная деятельность на уроках предполагает организацию и развитие диалогового общения, которое ведет к взаимопониманию, взаимодействию, к совместному решению общих, но значимых для каждого участника задач.
Диалог и полилог – это разные точки зрения, которые либо совпадают, либо нет; это активная интерпретация точки зрения другого; это ожидание ответа и его предвосхищение в собственном высказывании; это взаимодополнение точек зрения участников общения, а соотнесение этих точек зрения и является целью диалога и полилога.
Продуктивным приемам полилогического общения учащихся необходимо обучать. Это приемы работы, которые обеспечивают общий механизм функционирования группового общения. Среди них выделим приемы, направленные:
– на обучение запросу информации;
– на поддержание группового общения.
– на обучение принятию итогового решения по обсуждаемому вопросу.
На занятиях по математике участники полилога должны уметь суммировать наиболее продуктивные варианты решения задачи или поставленной проблемы сначала в микровыводы, а затем на основании этого делать общий вывод.
Диалоговое общение, в нашем представлении, может осуществляться в следующих вариантах: учитель ↔ ученик; учитель ↔ группа учащихся; ученик ↔ ученик; ученик ↔ группа учащихся; группа учащихся ↔ группа учащихся (схема 1).
Схема 1. Возможности осуществления диалогового общения между учителем и учащимися
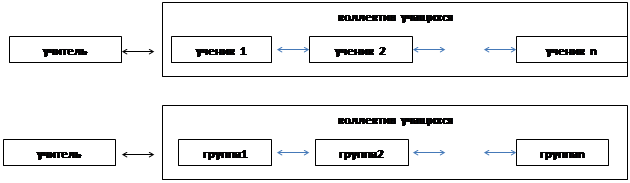
Кроме этого можно выделить следующие варианты осуществления диалогового общения: ученик ↔ компьютер; группа учащихся ↔ компьютер и др.
Включение исследовательских вопросов в диалог на уроках математики приводит обучающихся к размышлению, анализу, доказательству, выбору варианта ответа. Именно поиск ответа способствует развитию мышления, самостоятельной деятельности. Примерами таких вопросов могут служить следующие:
– Какими свойствами должен обладать четырехугольник, чтобы он являлся прямоугольником?
– Какие свойства должны быть присущи параллелограмму, чтобы он являлся прямоугольником?
– Как определить, является ли данный угол острым?
Анализируя задания учебников математики для общеобразовательной школы, можно сделать вывод о том, что большинство из этих заданий носят репродуктивный характер и имеют своей целью формирование знаний на уровне воспроизведения. А для развития самостоятельной деятельности обучающихся необходимы задания, побуждающие к действию. Сравним два задания:
1) Можно ли описать окружность около четырехугольника, углы которого равны 45 ° и 135 °?
2) Вокруг какой трапеции можно описать окружность?
В первом случае для решения задачи воспользуемся известным алгоритмом действий: 1) если данные углы противоположные, то найдем их сумму 45°+135°=180° и, воспользовавшись теоремой о сумме противоположных углов вписанного четырехугольника, ответим на поставленный вопрос; 2) если данные углы смежные, то однозначно ответить нельзя.
Во втором случае нет готового алгоритма решения задачи. Учащийся вынужден рассуждать, даже если он не знает, как решать эту задачу. Простой ответ – да или нет – будет получен в ходе внутреннего диалога учащегося с самим собой.
Интерактивное обучение исключает доминирование как одного участника процесса, так и одного мнения над другим. Одной из форм особой организации интерактивной деятельности обучаемых является «интерактивный урок».
Так, все «интерактивные уроки», например, открытия нового знания, по указанным выше учебникам, строятся на основе подводящего диалога, при этом структура каждого такого урока соотнесена со следующей схемой его построения:
· этап актуализации знаний (с соответствующей системой заданий);
· этап формулирования темы и целей урока на основании осознанного детьми противоречия (в результате созданной педагогом проблемной ситуации);
· этап первичного закрепления нового и первичной рефлексии;
· этап самостоятельной работы и развёрнутой рефлексии, ориентированной на осознание индивидуального уровня учебных достижений;
· этап дифференцированного развития учебных умений (с соответствующей системой заданий на трёх уровнях сложности).
Другой особой формой организации интерактивной деятельности учащихся на уроках геометрии является лабораторная работа.
Лабораторными работами в методической литературе называют проведение учащимися по заданию учителя опытов с использованием приборов, применением инструментов и других технических приспособлений, т.е. изучение учащимися каких-либо явлений с помощью специального оборудования. Впоследствии, лабораторными работами, в контексте нашего исследования, будем называть самостоятельное (в полной или частичной мере) решение учащимися задач, условия которых задаются различными предметами или специально для этого изготовленными моделями, чертежами для достижения определенных учебных целей. Урок – лабораторную работу можно считать видом урока совершенствования знаний, умений, навыков, а также можно отнести к типу урока контроля и коррекции знаний, умений и навыков. Кроме этого, лабораторные работы учитель может вводить в качестве элемента урока объяснения нового материала (при введении нового понятия, для иллюстрации какого-либо явления и т.п.) и в уроки-семинары, где они становятся одним из источников новых знаний. Оперирование наглядными пособиями, инструментами и т.д., как моделями реальных объектов, позволяет учащимся формировать пространственные образы.
Наглядные методы обучения отличаются от других методов тем, что источником информации при их использовании является наглядный образ, который возникает в процессе восприятия. Таким образом, восприятие составляет психологическую основу наглядных методов обучения. На уроках геометрии возможно использование различных геометрических моделей: сплошных, каркасных, прозрачных и др., изготовленных из различных материалов (пластилина, стекла, дерева и др.) или трехмерных компьютерных. Сплошная модель устраняет трудность представления самого геометрического тела, но не дает возможности зрительного прослеживания всех операций, значительная часть их должна выполняться в воображаемом геометрическом пространстве. Таким образом, значительная часть воображаемых операций уступает место операциям зрительным. В случае с прозрачной моделью мы имеем дело с усилением наглядности, и учащемуся остается лишь проследить взором те геометрические построения, которые были зафиксированы на предлагаемой геометрической модели. Но охарактеризованные модели не позволяют проследить перспективные изменения при их перемещении в пространстве. Однако, в ходе исследования, проводимого институтом психологии, было выявлено, что положительное влияние зрительной опоры на образовательный процесс имеет место только в том случае, если учитывать условия, от которых зависит тот или иной вероятный результат. Тогда восприятие модели помогает контролировать, какая из намеченных возможностей является наиболее эффективной. Таким образом, если человек не знает, как решать задачу, то зрительная опора может помочь делу.
Задача учителя математики, на наш взгляд, заключается в том, чтобы продумать четкую систему лабораторных работ в системе логически взаимосвязанных уроков геометрии, применение которых позволило бы ему обеспечить условия для организации и реализации процесса развития пространственного мышления.
Составной частью методов обучения являются приемы учебной деятельности учителя и учащихся. Методическими приемами являются действия, способы работы, направленные на решение конкретной задачи. Лабораторным приемом мы будем называть прием, связывающий наглядные и практические методы, направленный на реализацию возможностей целенаправленного применения различных средств наглядности для решения практических задач. Одной из функций лабораторного приема является развитие пространственного мышления учащихся. Существует мнение педагогов, что единственным моментом, в котором лабораторные работы уступают остальным, выполняя функцию развития, является тот, что они не дают возможности развивать способности выражать мысли. С этим мнением можно поспорить.
Мы считаем, что можно реализовывать идеи интерактивного обучения и в процессе лабораторной работы.
Систематическое проведение лабораторных работ на уроках геометрии дает возможность широко практиковать их и как вид домашнего задания. Учителю необходимо тщательно отбирать математические факты, которые учащиеся смогут «открыть» самостоятельно в процессе домашней лабораторной работы, и предоставить им такую возможность.
Для повышения активности на уроках математики полезно предлагать учащимся различные материалы. Ими могут служить, во-первых, все естественные объекты, которые окружают школьника, и, во-вторых, к ним можно отнести «искусственные материалы». Последние называют наглядными или дидактическими пособиями.
Выделим виды дидактических пособий:
1. Дидактические пособия, находящиеся в окружающем мире (модели точки, прямой, плоскости и т.д.). Отыскание таких моделей всегда вызывает неподдельный интерес у школьников. Дополнительно такие примеры дают учащимся широкое представление о самом понятии.
2. Модели, изготавливаемые самими школьниками. Учащиеся самостоятельно могут выполнить модели многоугольников и многогранников, например, из картона, глины, пластилина и даже из дерева. Возможность исполнения геометрической модели собственными руками способствует развития пространственного мышления учащихся.
3. Дидактические пособия, изготовленные на предприятии. К таким наглядным материалам можно отнести модели конуса, цилиндра, шара, многогранников, многоугольников, окружности и др.
К наглядным пособиям, реализующим идею интерактивного обучения, необходимо отнести продукты мультимедиа технологий, 3D программы и т.д. Эти продукты могут быть разработаны как самими школьниками, учителями, так и программистами.
Например, программа GeoGebra позволяет включать учащихся в деятельность создания виртуальных инструментальных моделей пространственных конфигураций – двумерных проекционных изображений пространственных фигур, допускающую изменения ракурса изображения, дополнительные построения и исследования.
Данные модели могут выполнять не только компенсаторные, но и развивающие функции. Их основу составляют известные методические приемы «выход в пространство» и «уход на плоскость», реализуемые в самых разных формах.
При обучении геометрии можно также проводить «интерактивные уроки воображения», например, при изучении взаимного расположения прямых и плоскостей в пространстве. На таких уроках учащимся приходится много представлять.
Приведем примеры заданий для обсуждения:
1) Две плоскости параллельны. Как расположены прямые одной плоскости относительно прямых другой плоскости?
2) Дана прямая параллельная плоскости. Можно ли утверждать, что она параллельна любой прямой этой плоскости? Почему?
3) Даны параллельные прямая и плоскость. Как будет располагаться прямая, параллельная данной прямой относительно данной плоскости?
4) Даны перпендикулярные прямая и плоскость. Можно ли утверждать, что любая прямая, параллельная данной плоскости, пересечет данную прямую? Почему?
Кроме этого мы рекомендуем организовывать для учащихся графические и лабораторные работы по каждой теме. Приведем пример заданий графических работ по темам «Параллельность в пространстве», «Перпендикулярность в пространстве»:
Сделайте чертежи с данными обозначениями:
1) Плоскости α и β имеют общую прямую a, плоскости α и γ – общую прямую b, а плоскости β и γ параллельны.
2) Прямая КМ перпендикулярна к плоскости квадрата KTPC, а прямая МА перпендикулярна к прямой СТ.
Все обсуждения проходят в интерактивном режиме.
Особое значение в современном образовании имеет организация исследовательской и проектной деятельности учащихся.
Учащимся с достаточно высоким уровнем пространственного мышления в качестве исследовательских заданий можно предложить следующие:
1) Как могут располагаться в пространстве два отрезка, чтобы их параллельными проекциями были: отрезок; отрезок и точка, не принадлежащая ему; две точки; одна точка?
2) Постройте ортогональную проекцию правильной четырехугольной пирамиды SABCD с вершиной S на плоскость, расположенную: а) параллельно основанию; б) параллельно диагональному сечению; в) параллельно боковой грани; г) параллельно ребру SA и на одинаковом расстоянии от вершин B и D; д) параллельно ребру SA и на разном расстоянии от точек B и D.
Темой проектного задания для группы учащихся или исследовательской работы учащихся может служить «Изображение геометрических фигур в центральной проекции». Примером рассматриваемой в этой теме задачи является следующая: «Как может располагаться в предметной плоскости aотрезок, чтобы его центральной проекцией были: луч; два луча?»
Особое внимание мы хотим обратить на особенности обучения математике по учебникам нового поколения, авторами которых являются С. А. Козлова, А. Г. Рубин, В. А. Гусев и др. Данные учебники соответствуют современным целям образования, ориентированы на развитие мышления (в т.ч. пространственного) и творческих личностных качеств, интереса к математике, формирование ключевых деятельностных компетенций и готовности к саморазвитию. Кроме этого, методическими особенностями указанных учебников и работы по ним являются:
1) мотивированное и доступное изложение теоретических сведений, способствующее пониманию и осознанности при усвоении материала;
2) целенаправленное обучение приемам и способам рассуждений, что позволяет обогатить интеллектуальный багаж школьников, способствует развитию мышления;
3) создание дидактических условий для формирования навыков исследовательской деятельности, самостоятельности мышления, творческих способностей;
4) живой, эмоциональный язык, использование современных сюжетов в теории и задачном материале, а также наличие интересных для учащихся форм подачи материала.
Работа по учебникам нового поколения подразумевает внедрение инновационных методов обучения – методов, ориентированных на введение инноваций в образование, и уже сама является инновацией.
По данным учебникам предусмотрена совместная с учителем учебно-познавательная деятельность, работа в группах, самостоятельная и проектная работа учащихся.
Учащимся заранее сообщается, какой теме будет посвящено следующее занятие, у них появляется возможность познакомиться заранее с имеющимся материалом и настроиться, таким образом, на обсуждение вопросов.
Обсуждение вопросов происходит в форме диалога или полилога при групповой или коллективной работе.
Считаем целесообразным активно внедрять интерактивные формы обучения и на других видах занятий.
Развитие пространственного мышления учащихся представляет одну из самых трудных задач обучения математике в средней школе. Использование данной системы в работе с учащимися способствует тому, что процесс развития становится более продуктивным: учащиеся начинают свободно оперировать свойствами и отношениями пространственных объектов, преобразовывать трехмерные образы в двумерные, и наоборот.
Рецензенты:
Гусев Валерий Александрович, доктор педагогических наук, профессор, заведующий кафедрой теории и методики обучения математике Московского педагогического государственного университета, г. Москва.
Санина Елена Ивановна, доктор педагогических наук, профессор, профессор кафедры психологии и педагогики Российского университета дружбы народов, г. Москва.
Библиографическая ссылка
Василенко А.В. ИННОВАЦИОННЫЕ ПОДХОДЫ В РАЗВИТИИ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ УЧАЩИХСЯ ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЫ // Современные проблемы науки и образования. 2013. № 3. ;URL: https://science-education.ru/ru/article/view?id=9431 (дата обращения: 13.03.2026).



