Введение
Стремительному развитию средств бизнес-аналитики и интеллектуального анализа данных [3] сопутствует развитие таких методов поддержки аналитической работы с данными, как визуализация данных и визуальная аналитика, которые позволяют наглядно представить большие массивы числовой и другой информации в интуитивно понятной и информативной визуальной форме.
Объектом настоящего исследования является система управления большими массивами показателей в научно-технической сфере. Примерами таких показателей являются индикаторы научно-технического потенциала развития науки и техники, содержащиеся в базах данных федеральных целевых научно-технических программ: базе заявок на формирование тематики и объемов финансирования работ и проектов, базе заявок на участие в конкурсе, базе государственных контрактов, заключенных государственным заказчиком, и базе результатов выполненных работ.
Предмет исследования – методы и средства визуализации структурированных данных, базовым формализмом для моделирования которых является граф как совокупность объектов и связей между ними.
Методы визуализации графов разрабатываются с начала 60-х годов XX века [6]. Мощный импульс развития направление исследований получило с появлением первых подходов на основе физических аналогий – «пружинных» алгоритмов Eades (1984), Kamada-Kawaii (1989) и Fruchterman-Reingold (1991). Среди алгоритмов, имеющих линейно-логарифмическую сложность, можно выделить многоуровневый алгоритм Yifan Hu, алгоритмы Force Atlas 2 и Open Ord (2011). В 1998 году в самостоятельное направление выделилась визуализация информации (в первую очередь текстовой), и всего несколько лет назад – визуальная аналитика. В фокусе современных исследований – методы визуализация больших графов, методы навигации при визуализации графов [1], методы визуализации социальных сетей. Основные результаты в этой области публикуются в международных изданиях Journal of Graph Algorithms and Applications, IEEE Transactions on Visualization and Computer Graphics, трудах Graph Drawing Symposia, IEEE Information Visualization Conference и других научно-технических мероприятий.
Цель исследования. Обоснование выбора методов, алгоритмов и программных средств с открытым исходным кодом для визуализации больших массивов научно-технических показателей в виде графов.
Методология исследования. Методы визуализации, теория графов и гиперграфов, теория баз данных.
Графы и гиперграфы специального вида для задач разметки и визуализации данных
Научно-технические показатели одной категории зачастую являются атрибутами различных сущностей и располагаются в разных таблицах в одной или в разных базах данных. Аналитикам же хочется видеть близкие по смыслу данные рядом. Процесс работы с исходными базами данных посредством группирования близких по смыслу атрибутов назовем выделением смысловых групп.
Для представления и визуализации связей как внутри одной смысловой группы, так и в нескольких группах обратимся к математическому аппарату теории графов и гиперграфов. Основное отличие гиперграфов [4] от графов заключается в том, что ребро гиперграфа может соединять не две, а большее число вершин. И хотя любой гиперграф можно представить в виде двудольного графа, а затем применить широкий спектр алгоритмов на графах, гиперграфы являются иным уровнем представления и хорошо понятны для аналитиков. Для отображения более полного спектра связей между компонентами данных может потребоваться использование некоторых дополнительных уточнений графовой парадигмы. Это могут быть ориентированные гиперграфы, GH-гиперграфы специального вида [5] и нечеткие графовые модели [2].
Выделим типы связей, которые могут быть использованы для представления и визуализации данных.
Неориентированные связи между простыми компонентами данных. Две вершины связаны неориентированным ребром, все связи в графе имеют одинаковый смысл («принадлежать к», «быть частью» – «состоять из»). Связь типа «gv-gv» (gv – graphvertex), представляется при помощи матриц (таблиц) инцидентности (Gv×Ge определяет, какое ребро связывает какие две вершины, где edge – ребро, vertex – вершина, Gv – множество вершин графа, Ge – множество ребер графа) или смежности (Gv×Gv определяет, какая вершина связана с какой вершиной; в неориентированном графе матрица смежности симметрична относительно диагонали, т.е. существуют связи gvi→ gvj и gvj→ gvi, элементы матрицы Gv×Gv gvij=gvji=1).
Ориентированные связи между простыми компонентами данных. Две вершины связаны ребром, все связи в графе имеют одинаковый смысл. Например, указание влияния, убывание/возрастание степени общности, обозначение последовательности процессов и т.д. Представляются также матрицами Gv×Ge и Gv×Gv, но матрица смежности не симметрична – при наличии связи gvi→ gvj, gvij=1, gvji=0.
Ориентированные и неориентированные связи между простыми компонентами данных. В графе присутствуют группы связей различных типов: «gv-gv» и «gv→gv». Например, на одном и том же множестве вершин одним типом связей представлены отношения персон в штатной структуре, другим типом – отношения во временном трудовом коллективе.
Каждая ориентированная или неориентированная связь графа имеет свое смысловое значение. В графе присутствуют группы связей различных типов: «gvi-tk-gvj» и «gvi-tk→gvj». Например, на одном и том же множестве вершин различными видами связей представлены отношения персон. На рис. 1 {A, B, C, D} – множество типов связей. Матрица Gv×Gv состоит из идентификаторов типов связей, 0 – отсутствие связи.
Неориентированные ребра гиперграфа представляют подмножества некоторого множества. Связь типа «hv-he» (h – hypergraph) представляется при помощи матриц инцидентности Hv×He, которые определяют, какое ребро какие вершины связывает. Например, пересечение областей научных интересов, где предметная область – ребро, вершины – индивиды.
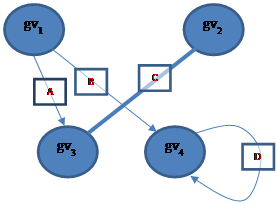
Рис. 1. Граф с группами связей различных типов
В ориентированных ребрах гиперграфа выделяется одна из вершин, которая имеет особый статус. Связь типа «hv-he*». Связи внутри ребра типа «все к одному» (рис. 2). Например, руководитель научной школы.
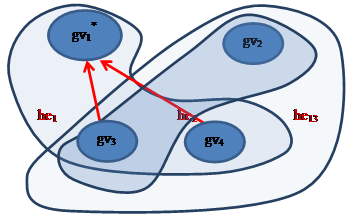
Рис. 2. Ориентированный гиперграф
Сложные связи внутри ребер гиперграфа. Графовые связи внутри ребра здесь не следует рассматривать как самостоятельные, они лишь описывают некоторые свойства конкретного ребра. Например, ребро гиперграфа – это конкурс, а вершины ребра – заявки, связанные внутри ребра гиперграфа ориентированными простыми (графовыми) ребрами в порядке возрастания значений некоторого параметра. Матрица инцидентности графа может содержать ссылки на матрицы смежности, описывающие отношения вершин внутри конкретного ребра.
«Графовые» связи между вершинами, входящими в разные ребра гиперграфа. Например, ребра гиперграфа – научные школы, вершины – индивиды, межреберные связи – связи цитирования.
Связи между ребрами гиперграфа. Например, ребра гиперграфа – стадии жизненного цикла заявки-вершины. Представляются несколькими матрицами инцидентности.
Развивая парадигму ориентированного гиперграфа [2; 4], предположим, что отношения вершин гиперграфа представлены неполным графом. Такая модель может отображать как отношения целых групп элементов, так и отношения между отдельными элементами.
Обобщенным гиперграфом назовем тройку следующего вида:
HX=(X,E , Gh (X)), X={x1, x2 ,…,xn}, E ={E1, E2 ,…,Em}, E1, E2 ,…,Em![]() X,
X,
Gh (X)=(X,U), U={u1,u2 ,…,ul,…,us}, ul=(xi, xj), xi, xj![]() X. (1)
X. (1)
Такое определение оставляет возможность представления отношений между вершинами разных ребер гиперграфа.
Частный случай обобщенного гиперграфа представлен определением (2). Он подразумевает графовые отношения только внутри ребер гиперграфа:
HX=(X,EX),X={x1, x2 ,…,xn}, EX = {(E1,GE1), (E2,GE2),…,(Er,GEl),…,
(Em,GEm)}, E1, E2 ,…, Er ,…,Em![]() X,GEr=(Er,Ur),Ur={u1,u2 ,…,ul,…,uk},ul=( xi, xj), xi, xj
X,GEr=(Er,Ur),Ur={u1,u2 ,…,ul,…,uk},ul=( xi, xj), xi, xj![]() Er. (2)
Er. (2)
Пример обобщенного гиперграфа показан на рис. 3.
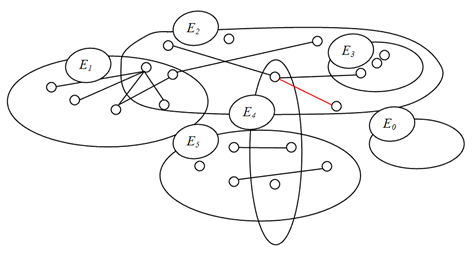
Рис. 3. Пример обобщенного гиперграфа
Нетрудно предположить, каким образом будет выглядеть таблица смежности нечеткого обобщенного гиперграфа. В ней должны присутствовать элементы следующих видов <µU(xi, xk)/(xi, xk)>, <µX(xi )/(xi)>, <µEi(xi )/(xi)>.
На рис. 4 предлагается пример представления обобщенного гиперграфа HX1. На представление гиперграфа HX1 двудольным графом GK=(XUEX ,V) наложены «графовые» связи вершин GS=GKUGE1UGE2,…,GEl),…, GEm.
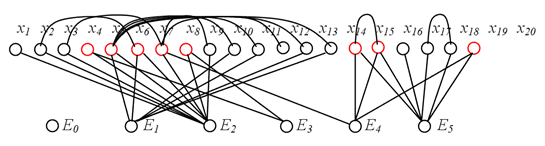
Рис. 4. Обобщенный гиперграф HX1
Предлагаемая модель позволяет отображать более сложные функциональные и смысловые связи между объектами.
Программное решение для визуализации и анализа больших массивов научно-технических показателей в виде графов
Разрабатываемое программное решение имеет клиент-серверную архитектуру (рис. 5).
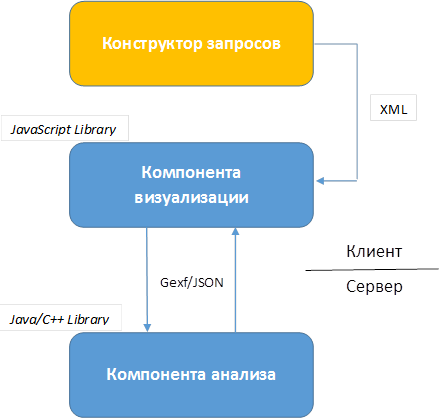
Рис. 5. Архитектура системы визуализации и анализа больших массивов научно-технических показателей в виде графов
Компонента визуализации работает на стороне клиента с использованием технологий HTML5 и JavaScript. Она предоставляет пользовательский интерфейс для формирования в режиме онлайн графового набора данных из реляционной таблицы, полученной по результатам работы конструктора запросов. Граф формируется последовательно с помощью несложных манипуляций на экране мобильного устройства. Поскольку даже небольшое замедление при формировании графа будет сказываться на удобстве работы пользователя, компонента визуализация должна поддерживать базовые операции на графах (добавление/удаление вершин и связей) и быстрые алгоритмы укладки, обеспечивающие отрисовку графа в реальном времени без запросов к серверу.
Серверная компонента анализа должна поддерживать дополнительные наглядные виды укладки сложных графов на плоскости, а также раскраску и ранжирование размера вершин на основе метрик центральности, фильтрацию, построение эго-сети, кластеризацию вершин, визуализацию картографической информации. На вход компоненты анализа поступает исходный граф в формате GEXF/JSON, задающий множество вершин и связей между ними, а на выходе – результирующий граф в формате GEXF/JSON для отрисовки, в котором для каждой вершины уже определены все атрибуты визуализации, включая тип, цвет, размер и позиционирование вершины в пространстве.
Заключение
С целью представления и визуализации связей между научно-техническими показателями внутри одной смысловой группы или в нескольких группах введено понятие обобщенного гиперграфа специального вида, который позволяет отображать более сложные функциональные и смысловые связи между объектами. Дана классификация типов связей, которые могут быть использованы для представления и визуализации данных.
Разрабатываемый программный комплекс имеет клиент-серверную архитектуру с компонентой визуализации на стороне клиента, реализуемой средствами HTML5 и Javascript, и компонентой анализа на стороне сервера с использованием внешней Java-библиотеки Gephi Toolkit. В качестве формата хранения и обмена графовыми данными между компонентами рекомендуется использовать формат GEXF.
Работа выполнена при финансовой поддержке Минобрнауки России по государственному контракту от 10 августа 2012 г. № 14.514.11.4037 в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы».
Рецензенты:
Карелин Владимир Петрович, д.т.н., профессор, заведующий кафедрой прикладной математики и информационных технологий НОУ ВПО «Таганрогский институт управления и экономики», г. Таганрог.
Ромм Яков Евсеевич, д.т.н., профессор, заведующий кафедрой информатики ФГБОУ ВПО «Таганрогский государственный педагогический институт имени А.П. Чехова», г. Таганрог.
Библиографическая ссылка
Целых А.А., Целых А.Н., Матвеев Д.А. МЕТОДЫ И СРЕДСТВА ВИЗУАЛИЗАЦИИ МАССИВОВ НАУЧНО-ТЕХНИЧЕСКИХ ПОКАЗАТЕЛЕЙ В ВИДЕ ГРАФОВ // Современные проблемы науки и образования. 2013. № 3. ;URL: https://science-education.ru/ru/article/view?id=9421 (дата обращения: 22.02.2026).



