Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Беляков А.К. 1 Крицына Н.А. 2 Кулябичев Ю.П. 2 Суханов А.А. 2

---

1 ОАО "Концерн "СИСТЕМПРОМ"

2 Национальный исследовательский ядерный университет (МИФИ)

Рассматривается метод формирования оптимальной упорядоченной выборки М точек из общего набора интерполяционных точек кривой, обеспечивающих минимум интеграла квадрата ошибки интерполя-ции. Для решения задачи предлагается критерий, представленный в виде суммы частных интегральных критериев. Данный подход позволяет использовать для решения общей оптимизационной задачи прин-цип дискретного динамического программирования Беллмана. Предлагаемый метод разрабатывается для использования в геоинформационных системах при формировании баз данных, содержащих интер-поляционные точки линий (дорожная сеть, различные границы и прочие линейные объекты) для после-дующего их отображения на карте местности. А также для предварительной фильтрации данных, вы-званной ограничениями оперативной памяти при использовании в специализированных навигационных устройствах.

Статья в формате PDF

211 KB

узловые точки

граф решения

критерий оптимизации

интерполяция

геоинформационная система

динамическое программирование

1. Бабич О.А. Обработка информации в навигационных комплексах. - М. : Машинострое-ние, 1991. - 512 с.

2. Крицына Н.А. Оптимизация параметров численного решения уравнений динамики // Алгоритмы цифрового оценивания, контроля и управления : сб. науч. трудов / под ред. д.т.н,, профессора Иващенко Н.Н. – М. : АТОМИЗДАТ, 1990, – 180 с.

3. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. — М. : Наука, 1978.

4. Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирование: моде-ли и вычислительные алгоритмы : учеб. пособие. — Изд. 2-е, испр. — М. : ФИЗМАТЛИТ, 2003. — 240 с.

5. Таха Х. Введение в исследование операций : в 2-х кн. / пер. с англ. – М. : Мир, 1985. - 496 с. : ил.

В настоящее время геоинформационные системы нашли широкое применение в различных областях деятельности. Как правило, в геоинформационных системах границы областей и фронтов распространения различных физических процессов, линии уровня рельефа местности, траектории движения подвижных объектов и т.д. отображаются на карте с помощью сплайн-интерполяции выбранного порядка по упорядоченному множеству , состоящему из N точек (N - большое число). Причем многие из этих точек являются избыточными и могут быть выведены из базы данных без существенной потери точности интерполяции.

В этой связи актуальной становится задача определения упорядоченного набора M точек из первоначального множества точек , (). В качестве критерия выбора точек рационально поставить условие минимизации площади, находящейся между линией, построенной по M упорядоченным точкам (линия ), и линии, построенной по N упорядоченным точкам (линия ). Такой критерий эквивалентен интегралу квадрата отклонения точек линии от соответствующих точек линии (рис. 1).

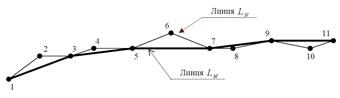
Рис. 1. Пример формирования линии .

Для примера: N=11, M=6.

Пусть , – число точек множества между точками множества , тогда справедливы следующие соотношения:

1. - первые и последние точки множеств и совпадают;

2. - узловые точки линий и совпадают.

Так как узловые точки совпадают, то общая площадь между линиями может быть представлена в виде суммы площадей, заключенных между узловыми точками. При этом критерий оптимизации выбора точек из множества запишем в виде суммы

(1)

где - площадь фигуры, находящейся между узловыми точками. .

Так как общее число точек множества равно , то нетрудно заключить, что если первые точек последовательностей совпадают, то интервал между последними точками и будет содержать точек множества , и, наоборот, если последние точек последовательностей совпадают, то интервал между первыми точками и будет содержать точек множества . Кроме того, общее число точек – N. Таким образом, ограничения, накладываемые на аргумент оптимизации, будут иметь вид:

, - целое число. (2)

. (3)

Представление критерия (1) в виде суммы дает основание использовать принцип метода дискретного динамического программирования [3; 4].

Решение данной оптимизационной задачи удобно представить в виде ограниченного графа на сетке решений (рис. 2) [2; 5].

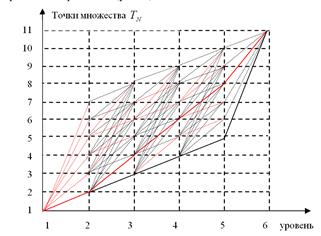
Рис. 2. Граф решения задачи методом дискретного динамического программирования.

Для примера:

Красной пунктирной линией отмечены «условно» оптимальные пути,

красной линией отмечен оптимальный путь.

По горизонтальной оси будем откладывать уровни решения задачи, причем число уровней соответствует числу точек множества ; по вертикальной оси – точки множества , в которые можно попасть на i-м уровне. Очевидно, в силу ограничений (2) и (3), каждый уровень (кроме первого и последнего) содержит точек.

Так как на первом уровне имеется единственная точка , то в точку второго уровня возможно попасть только единственным путем (рис. 2). При этом каждой точке уровня 2 будет соответствовать площадь фигуры , опирающейся на хорду между точками и (рис. 1). Значения этих площадей запоминаем.

При формировании третьего уровня в каждую точку уровня 3 возможно попасть многими путями из точек 2-го уровня (рис. 2). При этом каждому пути будет соответствовать свое значение суммы площадей

. (4)

(5)

Очевидно, чем больше номер , тем больше путей могут привести в эту точку, и тем больше различных значений площадей будет соответствовать этой точке. Выберем путь в точку , который соответствует минимальной площади. С этой целью для каждой точки найдем такое , которое обеспечивает минимум критерия (4),

, (6)

(7)

Полученные значения , запоминаем. На рисунке в качестве примера оптимальные пути для точек уровня 3 выделены красным цветом.

Описанную выше процедуру формирования точек уровня 3 повторяем для уровней В результате для уровня будем иметь следующие соотношения:

, (9)

(10)

Полученные значения , запоминаем.

Последний уровень M имеет только одну точку , попасть в которую можно из точек предыдущего уровня (рис. 2). Причем каждому пути будет соответствовать значение площади:

(11)

Найдем единственный путь, обеспечивающий минимум критерия (11):

, (12)

(13)

Используя соотношения (12), (9) и (6), пройдем весь путь по оптимальным точкам в обратном направлении:

(14)

Перечисленная в (14) последовательность будет оптимальным набором точек множества , обеспечивающих минимум критерия (1).

Зная номера точек множества , входящих в множество , нетрудно найти оптимальное число точек между узлами .

Приведенный алгоритм может быть применен в информационных системах различного назначения для «фильтрации» большого объема данных при обработке линейных объектов. В частности, маршрутов (треков), полученных с помощью автоматизированных средств записи перемещения объектов (GPS/ГЛОНАСС-приемники), для уменьшения времени обработки изображений различных линейных объектов в ГИС.

Кроме того, многие специализированные навигационные устройства позволяют загружать в память пути (треки) с ограниченным количеством точек (например, максимальное количество точек пути, которые можно загрузить в популярные устройства серии FORERUNNER производства компании GARMIN составляет 500 точек). Приведенный метод позволяет осуществлять предварительную обработку данных для загрузки в такие устройства [1]. Особенностью метода является максимальное сохранение степени кривизны исходного линейного объекта при заданном уровне фильтрации.

Рецензенты:

Загребаев Андрей Маркоянович, д.т.н., профессор, Национальный исследовательский ядерный университет (МИФИ), г. Москва.

Крянев Александр Витальевич, д.ф-м.н., профессор, Национальный исследовательский ядерный университет (МИФИ), г. Москва.

Библиографическая ссылка