Введение
Для обеспечения надежности всей энергетической системы используются вакуумные выключатели. Для включения вакуумных выключателей целесообразно применять электромагнитные приводы от емкостных накопителей, например конденсаторов, способных потреблять электроэнергию с меньшими мощностями, которые имеют ряд преимуществ: имеют наименьшее количество деталей, повышая уровень надежности, просты в изготовлении, имея одну подвижную деталь – якорь, наименее габаритные [1; 4].
Математическое описание процесса включения выключателя с электромагнитным приводом от емкостного накопителя представляет значительные трудности, т.к. задача получается многофакторной в силу нелинейности следующих элементов: нелинейности кривой намагничивания материала магнитопровода электромагнита и изменения его индуктивности в процессе включения, сопротивления пружин поджатия и отключения. В связи с этим становится актуальным теоретическое изучение физических процессов, происходящих в электромагнитном приводе вакуумного выключателя (ЭПВВ).
Цель исследования
Целью исследования является построение и исследование математической модели ЭПВВ, расчет магнитного поля системы сложной конфигурации с последующим расчетом динамики изменения переменной индуктивности. Исследование осуществляется на примере модельного вакуумного выключателя типа ВБСК-10-20/1000, соответствующего реально используемому на практике устройству [5].
Вывод основных соотношений
На рисунке 1 представлена упрощенная модель электромагнитного привода вакуумного выключателя. Для описания процессов, происходящих в электромагнитном приводе, представим его как электромеханическое устройство [3].
На том же рисунке приводится электротехническая схема замещения, в которой 
– емкость батареи конденсаторов, 
– переменная индуктивность электромагнитного привода, 
– сопротивление, 
– начальная индуктивность катушки.
Для математического описания рассматриваемого устройства необходимо иметь величины параметров 
электромеханической модели. Приведем их описание.
В электротехнической схеме батарея конденсаторов емкостью 
заряжается до напряжения 
. Энергия электростатического поля, запасенная в конденсаторе, передается в электрическую цепь. Сопротивление цепи будем считать равным 
. Далее необходимо рассчитать два следующих параметра: и 
.
Катушка имеет сложную конфигурацию электродов, поэтому расчет индуктивности катушки в работе проведен через известное энергетическое соотношение, в соответствии с которым:
, (1)
здесь 
– ток в цепи, 
– энергия магнитного поля, – индуктивность.
а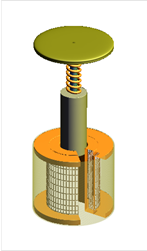 
б 
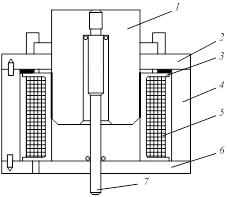в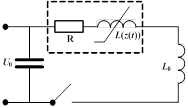 
1) якорь (сталь); 2) плита верхняя (сталь); 3) каркас катушки (дерево); 4) плита боковая; 5) токовая обмотка из меди; 6) плита нижняя; 7) вал (дерево)
Рис. 1. Упрощенная модель электромагнитного привода вакуумного выключателя: а) сечение электромагнитного привода; б) модель электромагнитного привода; в) электротехническая схема замещения привода
В свою очередь энергию магнитного поля при заданной конфигурации электродов и заданном распределении токов можно определить, используя последовательность соотношений [6]:
, (2)
где 
– векторный магнитный потенциал, 
– вектор плотности тока.
Апробация метода была произведена на примере цилиндрической катушки с многослойной обмоткой прямоугольного сечения [2].
Используя (2) и рис. 1б была получена расчетная формула (3) для расчета индуктивности катушки на основе расчета электромагнитного поля [2]:
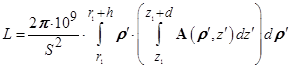, (3)
где 
- площадь сечения; 
- внутренний радиус; 
- высота обмотки; 
- ширина обмотки; 
- нижний предел интегрирования по оси 
; 
- функция распределения векторного потенциала, пространственный вид которого представлен на рис. 3; 
- радиус элементарной кольцевой трубки тока; 
- переменная интегрирования вдоль оси ; 
- сечение элементарной кольцевой трубки тока.
Расчет поля векторного потенциала проведен на основе метода конечных элементов в программе MATLAB в декартовой системе координат и, используя сплайновую технологию, преобразован в цилиндрическую систему координат. Результаты расчетов приведены ниже (рис. 3).
Алгоритм для расчета динамической индуктивности ЭПВВ в программно-интегрированных средах MATLAB и MathCAD
- Ввод данных: геометрические размеры установки, плотность тока, магнитная проницаемость, граничные условия.
- Построение геометрической конфигурации установки и граничные условия области.
- Учет неоднородного распределения псевдомагнитной проницаемости.
- Триангуляция области со сложной геометрией электродов в плоскости.
- Расчет поля распределения потока магнитной индукции.
- Преобразование триангулированной сетки в прямоугольную сетку.
- Пересчет полученных величин из декартовой системы в цилиндрическую систему.
- Расчет поля распределения векторного магнитного потенциала.
- Сохранение данных в текстовом документе в кодах ASCII.
- Перевод данных в среду MathCAD.
- Преобразование дискретных значений поля в непрерывные с помощью сплайновой аппроксимации.
- Апробация алгоритма с помощью справочных данных
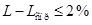. - Выход: расчет динамики изменения индуктивности катушки.
Новизна алгоритма заключается в пересчете результатов решения из декартовой системы координат в цилиндрическую систему на основе введения неоднородного распределения псевдомагнитной проницаемости.
На рис. 2 показан интерфейс программы, позволяющей рассчитывать индуктивности коаксиальных устройств, в том числе и переменную индуктивность катушки электромагнитного привода вакуумного выключателя (ЭПВВ) (левое окно), где:
y1 – начальное положение нижней границы якоря (ЭПВВ);
y2 – конечное положение нижней границы якоря (ЭПВВ);
h – шаг;
m - магнитная проницаемость;
j - плотность тока.
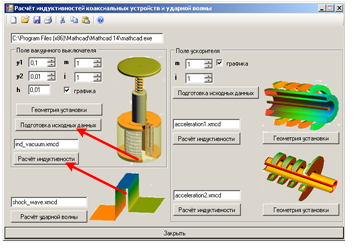
Рис. 2. Интерфейс программы для расчета индуктивностей коаксиальных устройств
Методика исследования
На рисунке 3 представлено распределение векторного потенциала в зависимости от положения якоря и соответствующее значение индуктивности.
а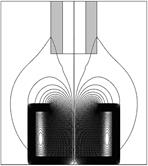 
б 
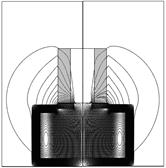в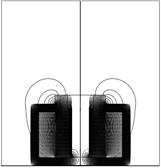 
Рис. 3. Распределение векторного потенциала поля при различном положении якоря и соответствующее значение индуктивности катушки: а) 
; б) 
; в) 
Начальная индуктивность катушки, рассчитанная по разработанному алгоритму, равна . При движении якоря в сторону стопа индуктивность сначала плавно увеличивается, затем резко возрастает почти в 20 раз.
Динамику изменения расположения якоря по отношению к катушке можно проследить на рисунке 4:
а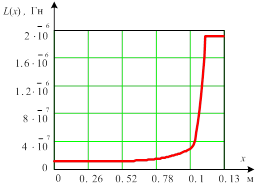
б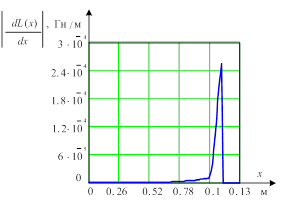 
Рис. 4. Динамика изменения расположения якоря по отношению к катушке: а) зависимость индуктивности 
от положения якоря 
; б) зависимость производной индуктивности 
Таким образом, в DLL MATLAB было получено распределение векторного потенциала поля исследуемой модели. Дискретные значения индуктивности с помощью кубической сплайновой аппроксимации преобразовывались в непрерывные. Получена начальная индуктивность катушки, используя уравнение (3) и зная геометрические параметры катушки:
.
Математическая модель ЭПВВ
На основе уравнения Лагранжа с использованием второго закона Кирхгофа и второго закона Ньютона получена система нелинейных дифференциальных уравнений (4), которая решена численно, для повышения точности расчета она предварительно была сведена к системе дифференциальных уравнений первого порядка:
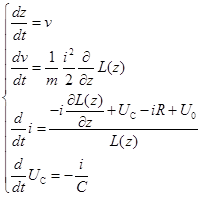в векторной форме 
, (4)
здесь 
– вектор состояния содержит следующие компоненты: 
– координату, 
– скорость, 
– ток и 
– напряжение на конденсаторе; 
– расширенная матрица. После расчета основных величин 
полезно рассчитать вспомогательные величины: кинетическую энергию движения якоря 
, магнитную энергию индуктивности 
, электрическую энергию конденсатора 
, омическую энергию потерь 
(рис. 5).
В качестве правильности работы алгоритма расчета была проведена проверка баланса энергии (5) рассматриваемой системы (рис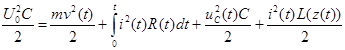. 5):
. (5)
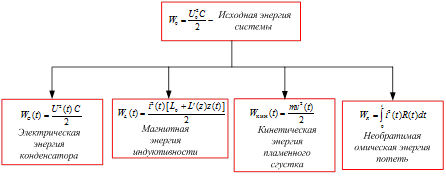
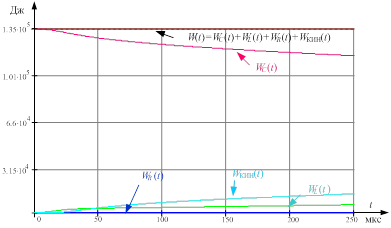
Рис. 5. Схема распределения энергии в плазменном ускорителе
Заключение
В работе предложена математическая модель для исследования процессов, происходящих в ЭПВВ, и алгоритм расчета электрических и кинематических параметров на основе использования представленной электротехнической схемы замещения (рис. 1в).
Представлен алгоритм расчета переменной индуктивности катушки, имеющей сложную конфигурацию, на основе расчета энергии электромагнитного поля, в зависимости от положения якоря, получена зависимость производной индуктивности (рис. 4б).
Получено решение системы дифференциальных уравнений равновесия напряжения и тока в цепи, установлена ее связь с механическими процессами в системе.
В качестве правильности работы алгоритма расчета проведен расчет баланса энергии рассматриваемой системы.
Рецензенты:
Сивков А.А., д.т.н., профессор кафедры ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Новиков С.А., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Васильева О.В. МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПРИВОДА ВАКУУМНОГО ВЫКЛЮЧАТЕЛЯ // Современные проблемы науки и образования. – 2013. – № 3. ;URL: https://science-education.ru/ru/article/view?id=9347 (дата обращения: 13.10.2024).