Главными показателями эффективности торможения автотранспортных средств (АТС) рабочей тормозной системой являются время срабатывания тормозной системы и тормозная сила между колесом и опорной поверхностью, пропорциональная тормозному моменту и, соответственно, силе нажатия на тормозную колодку.
Быстродействие гидромеханической тормозной системы, которой оснащается подавляющее большинство современных АТС, в лучшем случае составляет 0,2 с. Прогрессивный электрогидравлический тормозной привод по результатам испытаний способен создавать максимальное давление в тормозной системе до 150·105 Па за 0,1 с [5].
Повышение безопасности дорожного движения в современных условиях предъявляет ещё более высокие требования к эффективности торможения АТС – время срабатывания тормозной системы менее 0,1 с при силе нажатия на тормозную колодку порядка 25-30 кН. При меньшей силе тормозной момент может оказаться недостаточным, особенно при экстренном торможении.
Электромеханический тормозной привод, подобно электрогидравлическому, построен по модульному принципу, но вместо гидроцилиндров в колесных тормозных модулях установлены электродвигатели с исполнительными механизмами. Двигатели связаны с датчиками, электронным блоком управления и аккумуляторной батареей только электрическими проводами. Из-за отсутствия промежуточных звеньев (гидронасоса, электромагнитных клапанов) прогнозируемое время срабатывания электромеханического тормозного привода меньше, чем у электрогидравлического. Кроме того, он легко встраивается в антиблокировочную систему автомобиля [4]. Поэтому над созданием перспективных электромеханических тормозных приводов ведутся работы во всем мире (фирмы Bosch, Lucas Varity, ContiTeves, Mercedes-Benz, Tojota). Однако до сих пор эти разработки не вышли из стадии экспериментальных, так как к электромеханическому тормозному приводу предъявляются весьма высокие и к тому же противоречивые требования. Нужен быстродействующий, силовой и вместе с тем компактный электропривод, который можно разместить в ограниченном пространстве обода колеса автомобиля. Такой привод может быть реализован при сочетании малогабаритного высокомоментного электродвигателя и малоинерционного исполнительного механизма, обладающего высокой редукцией, нагрузочной способностью и КПД.
Среди известных механических передач наиболее полно указанным требованиям удовлетворяют планетарные роликовинтовые передачи (ПРВП), представляющие собой одну из разновидностей передач винт-гайка качения для преобразования вращательного движения в поступательное [3].
ПРВП состоит из винта, ходовой и опорной гаек, резьбовых роликов с зубчатыми венцами на концах, которые входят в зацепление с зубчатыми венцами винта и опорной гайки для предотвращения проскальзывания роликов по виткам резьбы. Она удачно компонуется с вентильным двигателем серии ДБМ, так как может быть встроена в полый ротор, а ее винт выполнен заодно с валом двигателя, исключая промежуточный редуктор. Кроме того, конструкция вентильного двигателя этой серии оптимизирована по критерию максимума отношения пускового момента к массе [1].
При вращении винта резьбовые ролики, расположенные в пространстве между винтом и гайками, совершают планетарное движение, а ходовая гайка-шток, закрепленная от вращения, перемещается в осевом направлении вместе с рабочим органом (тормозной накладкой). После выборки конструктивного зазора между тормозной накладкой и опорной фрикционной поверхностью в колесе на штоке ПРВП возникает осевая сила (нормальная сила реакции опорной фрикционной поверхности), равная по величине силе нажатия на тормозную колодку.
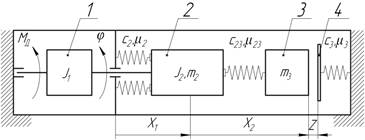
Рис. 1. Динамическая модель электромеханического тормозного привода. 1 – ротор электродвигателя; 2 – блок винта с роликами ПРВП; 3 – ходовая гайка-шток; 4 – опорная фрикционная поверхность.
Для оценки технического уровня спроектированного электромеханического тормозного привода [8] на базе ПРВП, обеспечивающей перемещение штока на 1 мм за оборот винта, и вентильного двигателя ДБМ120-1-0,8-2 необходимо проведение всестороннего динамического анализа привода. С этой целью, прежде всего, была построена его динамическая модель (рис. 1). Исполнительный механизм привода в виде ПРВП является многопоточным, но основная часть осевой силы, развиваемой на штоке, передается по цепи ходовая гайка – блок роликов – опорная гайка – корпус привода. На этом основании учитывались осевая податливость и диссипативные силы внутреннего трения в материале только звеньев, находящихся в наиболее нагруженной силовой цепи, а также потери на трение скольжения и качения в сопряжениях этих звеньев. Винт ПРВП, выполненный заодно с валом двигателя, воспринимает на два порядка меньшую нагрузку, следовательно, крутильной податливостью винта и роликов можно пренебречь.
В указанной постановке ПРВП представляет собой трехмассовую механическую систему с сосредоточенными параметрами, которая состоит из абсолютно твердых тел, соединенных между собой безынерционными упругодиссипативными элементами, подчинена стационарным голономным связям и обладает тремя степенями свободы.
При составлении дифференциальных уравнений движения ПРВП методом Лагранжа за обобщенные координаты принимались: φ – угол поворота винта ПРВП; x1 – линейная координата блока винта с роликами относительно корпуса; x2 – относительная координата ходовой гайки-штока, начало отсчета которой выбрано в положении ходовой гайки на блоке винта с роликами, соответствующем определенному углу φ при отсутствии осевой нагрузки на штоке. В результате получена математическая модель ПРВП в виде системы обыкновенных линейных дифференциальных уравнений шестого порядка с постоянными коэффициентами [7]:
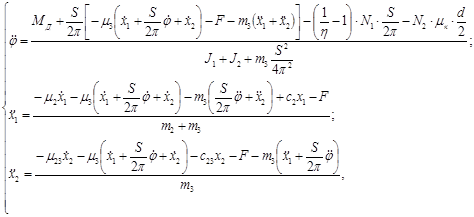 (1)
(1)
где МД – момент электродвигателя; J1 – момент инерции ротора электродвигателя; J2 – приведенный момент инерции блока винта с роликами; m2 – приведенная масса блока винта с роликами; m3 – приведенная масса ходовой гайки-штока и рабочего органа; c2 – линейная жесткость в сопряжении опорной гайки с роликами; c23 – линейная жесткость в сопряжении ходовой гайки-штока с роликами; c3 – линейная жесткость в сопряжении ходовой гайки-штока с опорной фрикционной поверхностью; μ2 – коэффициент демпфирования при осевой деформации деталей в сопряжении опорной гайки с роликами; μ23 – коэффициент демпфирования при осевой деформации деталей в сопряжении ходовой гайки-штока с роликами; μ3 – коэффициент демпфирования при осевой деформации деталей в сопряжении ходовой гайки-штока с опорной фрикционной поверхностью; μк – безразмерный коэффициент, учитывающий потери на трение качения в сопряжении опорной гайки с роликами; S – перемещение ходовой гайки-штока за оборот винта; d – средний диаметр резьбы опорной гайки; η – КПД ПРВП; ![]() – осевая сила в резьбовом сопряжении ходовой гайки-штока с роликами;
– осевая сила в резьбовом сопряжении ходовой гайки-штока с роликами; ![]() – осевая сила в резьбовом сопряжении опорной гайки с роликами; F – осевая сила на штоке ПРВП, если
– осевая сила в резьбовом сопряжении опорной гайки с роликами; F – осевая сила на штоке ПРВП, если ![]() , то
, то ![]() , иначе
, иначе ![]() , где z – зазор между тормозной накладкой и опорной фрикционной поверхностью.
, где z – зазор между тормозной накладкой и опорной фрикционной поверхностью.
Эти уравнения необходимо дополнить зависимостью МД от параметров движения, определяющей характер взаимодействия двигателя с ПРВП. Зададим эту зависимость нелинейной динамической характеристикой вентильного двигателя [2], которую представим в виде:
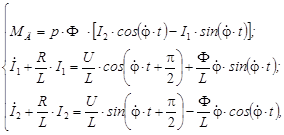 (2)
(2)
где Ф – магнитное потокосцепление ротора; U – амплитудное значение напряжения на обмотках статора; L – индуктивность рассеяния фазы обмотки статора; R – активное сопротивление фазы обмотки статора, p – число пар полюсов. Будем полагать, что в этой характеристике учтено и влияние сил сопротивления, действующих на звенья двигателя.
Исследование динамики тормозного привода состояло в анализе решений дифференциальных уравнений математической модели (1) и (2), соответствующих двум характерным переходным режимам его работы. Первый – режим неуправляемого разбега из состояния покоя при постоянном значении напряжения на обмотках статора электродвигателя и отсутствии сопротивления на штоке ПРВП до возникновения на нем осевой силы. За время этого переходного процесса тормозная накладка, перемещаясь в осевом направлении вместе с ходовой гайкой-штоком, выбирает конструктивный зазор и подходит к опорной фрикционной поверхности. Этот интервал времени называют временем запаздывания тормозной системы τc [6]. Второй – режим, при котором осевая сила на штоке ПРВП увеличивается от нуля до максимального установившегося значения (наброс нагрузки). Интервал времени, в течение которого достигается это значение осевой силы и соответствующее ей установившееся замедление АТС, называется временем нарастания замедления τн. Время срабатывания тормозной системы определялось как время работы привода на обоих режимах τср= τс + τн.
В связи с нелинейностью и достаточно высоким порядком системы дифференциальных уравнений математической модели тормозного привода их решение проводилось на ЭВМ с использованием разработанного программного обеспечения в среде программирования Delphi методом Рунге-Кутты четвертого порядка.
Построенный по результатам расчетов график зависимости осевой силы на штоке от времени (кривая 1 на рис. 2) наглядно иллюстрирует динамику срабатывания электромеханической тормозной системы. Кривая 1 построена при следующих параметрах привода: амплитудное значение напряжения на обмотках статора U = 27 В, соответствующий ему пусковой момент двигателя MД = 4,5 Н![]() м, приведенный к оси винта момент инерции привода J = = J1 + J2 +
м, приведенный к оси винта момент инерции привода J = = J1 + J2 + ![]() = 1,01·10-3 кг·м2, c3 = 9·106 Н/м, μ3 = 27.4·104 Н·с/м, z = 3·10-4 м. Для сравнения на том же рисунке приведены аналогичные графики, построенные по результатам испытаний электрогидравлической (кривая 2) и гидромеханической (кривая 3) тормозных систем [5]. Соответствующие этим графикам показатели эффективности торможения АТС тормозными системами различного типа сведены в таблицу 1.
= 1,01·10-3 кг·м2, c3 = 9·106 Н/м, μ3 = 27.4·104 Н·с/м, z = 3·10-4 м. Для сравнения на том же рисунке приведены аналогичные графики, построенные по результатам испытаний электрогидравлической (кривая 2) и гидромеханической (кривая 3) тормозных систем [5]. Соответствующие этим графикам показатели эффективности торможения АТС тормозными системами различного типа сведены в таблицу 1.
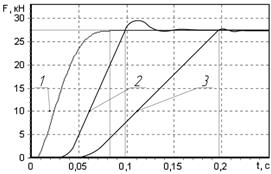
Рис. 2. Динамика срабатывания тормозных систем: 1 – электромеханической, 2 – электрогидравлической, 3 – гидромеханической.
Таблица 1. Показатели эффективности торможения АТС тормозными системами различного типа
|
Тип привода |
τс, с |
τн, с |
τср, с |
F, кН |
|
Электромеханический |
0,008 |
0,07 |
0,078 |
27 |
|
Электрогидравлический |
0,03 |
0,07 |
0,10 |
27 |
|
Гидромеханический |
0,05 |
0,15 |
0,20 |
18 |
Из таблицы следует, что расчетное время срабатывания τср электромеханической тормозной системы меньше на 22%, чем у электрогидравлической, и на 61%, чем у гидромеханической.
Заметим, что такое уменьшение τср достигается за счет уменьшения интервалов времени обоих переходных процессов как τс, так и τн. Кроме того, осевая сила на штоке спроектированного электромеханического тормозного привода F = 27 кН равна силе нажатия на тормозную колодку, которая обеспечивается электрогидравлическими тормозными системами АТС категории М1 при давлении 150·105 Па, и на 9 кН больше той, которая обеспечивается гидравлическими тормозными системами при площади типовой тормозной накладки 15·10-4 м2.
Математическое моделирование динамики электромеханического тормозного привода в широком диапазоне изменения параметров позволило установить, что определяющее влияние на время срабатывания тормозной системы и силу нажатия на тормозную колодку оказывают коэффициенты жесткости c3 и демпфирования μ3 в сопряжении штока с опорной поверхностью и приведенный момент инерции привода J. Установлен характер влияния каждого из этих параметров на время срабатывания тормозной системы.
На рис. 3, 4, 5 показаны графики зависимостей осевой силы на штоке от времени при различных значениях параметров c3, μ3, J соответственно. Для сравнения на каждом из рисунков кривая 2 та же, что кривая 1 на рис. 2.
Сравнительный анализ показал, что увеличение c3 и уменьшение μ3 сказывается на динамике срабатывания электромеханического тормозного привода, вызывая уменьшение интервала времени τср за счет уменьшения τн при неизменном τс (рис. 3, 4).
Уменьшение приведенного момента инерции привода Jпр по известным причинам приводит к уменьшению времени запаздывания тормозной системы τс и осевой силы на штоке (рис. 5). Вместе с тем, пропорционально приведенному моменту инерции привода, увеличивается динамическая составляющая осевой силы на штоке, что может привести к значительному увеличению времени срабатывания тормозной системы τср (кривая 3 на рис. 5).
Изменение конструктивного зазора z между тормозной накладкой и опорной фрикционной поверхностью мало влияет на время срабатывания тормозной системы τср. Так, при изменении z в 4 раза в диапазоне 0,15-0,6 мм τср изменяется лишь на 4·10-3 с в диапазоне 0,073-0,077 с. То же можно сказать о влиянии на τср жесткостей c2 и c23, а также коэффициентов демпфирования μ2 и μ23, величины которых на порядок превосходят c3 и μ3 соответственно.
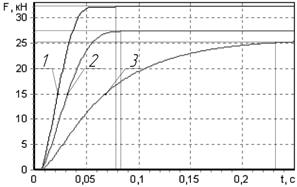
Рис. 3. Графики зависимостей осевой силы на штоке от времени при различных значениях с3(Н/м): 1 – c3 = 3.5·106; 2 – c3 = 9.0·106; 3 – c3 = 16.0·106.
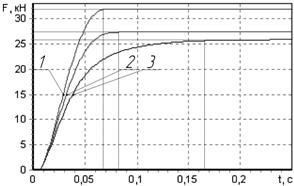
Рис. 4. Графики зависимостей осевой силы на штоке от времени при различных значениях μ3(Н·с/м): 1 – μ3 = 19·104; 2 – μ3 = 27.4·104; 3 – μ3 = 40·104.
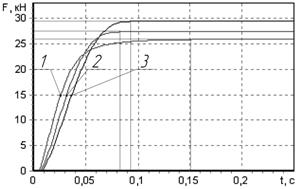
Рис. 5. Графики зависимостей осевой силы на штоке от времени при различных значениях J(кг·м2):
1 – J = 0.0005; 2 – J = 0.0010; 3 – J = 0.0015.
Осевая сила на штоке не зависит от параметров исполнительного механизма и полностью определяется пусковым моментом электродвигателя. Например, при пусковом моменте МД = 2,5 Н·м при прочих равных условиях на штоке развивается сила F = 12 кН, а при пусковом моменте МД = 4,5 Н·м осевая сила достигает F = 27 кН. Однако такое увеличение пускового момента связано с необходимостью повышения тока на обмотках статора и предъявляет повышенные требования к силовым транзисторам системы управления, которые, как показал опыт испытаний, могут выйти из строя.
Проведенный динамический анализ электромеханического тормозного привода показал его более высокий технический уровень по сравнению с электрогидравлическим и гидромеханическим приводами по таким качественным показателям, как время срабатывания и осевая сила на рабочем органе. Установлены конструктивные параметры электромеханического тормозного привода, при обоснованном сочетании которых на этапе проектирования возможно дальнейшее улучшение этих показателей.
Рецензенты:
Гоц, Александр Николаевич д.т.н., профессор кафедры тепловых двигателей и энергетических установок ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.
Кульчицкий Алексей Рэмович, д.т.н., профессор, главный специалист ООО «Завод инновационных продуктов», г. Владимир.
Библиографическая ссылка
Тутубалин Р.Ю., Филимонов В.Н. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ ЭЛЕКТРОМЕХАНИЧЕСКОГО ТОРМОЗНОГО ПРИВОДА // Современные проблемы науки и образования. 2013. № 3. ;URL: https://science-education.ru/ru/article/view?id=9207 (дата обращения: 22.02.2026).



