Введение. Болезни системы кровообращения (БСК) занимают первое место среди причин смертности во всем мире [3; 6]. Для получения оценок нормативных значений уровней заболеваемости, смертности и инвалидности от БСК и онкологических заболеваний на отдельных административных территориях применяют математические модели развития первичного заболевания по ограниченному числу наблюдений. На основе такого анализа принимаются меры по приведению медицинских служб в состояние, при котором локализуются причины и очаги роста заболевания [5; 8].
Цель исследования. Исследовать механизм и алгоритм построения образа обратного развития БСК и его представления по двум разнохарактерным группам исследования на основе его математического моделирования, численных методов расчета, программирования.
Материалы и методы исследования. В данной работе изучена и оценена динамика БСК в сравнении с онкозаболеваниями на территории Чувашской Республики, составлены и подготовлены таблицы по первичной заболеваемости, общей заболеваемости, смертности для сравнения. Рассчитаны показатели санитарной статистики за 10 лет. Далее нами были использованы методы математического анализа, методы абстрактной алгебры, приложения теории вероятности и математической статистики, методы теорий групп, групповых кодов, помехозащищенных кодов, помехоустойчивого кодирования.
1. Проведен анализ погрешностей и различия по критерию Стьюдента нормативных значений показателей первичной заболеваемости, общей заболеваемости и смертности в динамике развития БСК и новообразований, определяющих состояние здоровья населения. Вероятность, что гипотеза различия показателей по двум разнохарактерным группам исследования не подтвердится, рассчитывалась интегрированием функции T(x,N) распределения Стьюдента в пределах от -
до x. Рассчитываемые параметры: t – квантиль распределения Стьюдента по смыслу решаемой задачи является коэффициентом различия по критерию Стьюдента; p – уровень значимости, который связан с вероятностью попадания искомого значения q центральной статистики 
, определяющей гипотезы различия показателей по двум разнохарактерным группам исследования, в доверительный интервал Db с вероятностью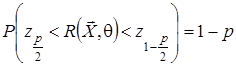 
. Значения 
и 
- квантили уровней p/2, 1–p/2 распределения T(x,N).
2. Использованы математические модели для оценки динамики заболеваемости и смертности от онкологических болезней и БСК и сравнения этих моделей для определения общего характерного контраста в развитии этих заболеваний. Суть математической модели сложного явления заключалась в привязке последнего по характерным признакам к известным структурам двоичного кодирования («Да» – 1, «Нет» – 0) из теории помехозащищенных кодов, описывающих пространство реализации некоторого множества квазиустойчивых, двухпозиционных состояний: включен, выключен. Для описания сложного явления здесь нами подключается весь аппарат генерации (создания) натуральных и ненатуральных групповых кодов разными методами. Это и получение новых кодов посредством декодирования линейных групповых кодов (ЛГК), и построение матриц ошибок разной кратности для ЛГК, и формирование кодов с малой плотностью проверок на четность, и создание циклических кодов.
Составим расчетный макет таблицы сравнения данных на листе автоматизированного расчета в Excel. Добавим еще два столбца к статистическим данным новой табл. 1: значения коэффициента различия по критерию Стьюдента t и достоверности различия p. Приведем сравнительный расчет первого столбца показателя – первичной заболеваемости населения соответственно по БСК и онкологии за 2001 год в исходной статистической таблице. Создадим для удобства ячейки сравнения со средними ошибками. Учтем, что при вычислении t масштабы самих показателей (не ошибки их) должны быть выровнены. Рассчитаем вероятность и уровень значимости, квантили распределения. Составим алгоритм предварительного проверочного расчета квантилей распределения Стьюдента T(x, n) при n=8. Поставим управляющую командную кнопку «Расчет квантиля T(n) для уровня p» автоматизированного расчета на листе Excel. Напишем программу с использованием алгоритма численного расчета p методом Рунге-Кутта 4 степени точности [4].
Таблица 1
Оценка достоверности различия показателя первичной заболеваемости БСК и онкологией (на 10 тыс. населения) с расчетом их веса в процентах (частоты и ошибки показателя) по 26 группам (в 19 районах и 5 городах) Чувашской Республики
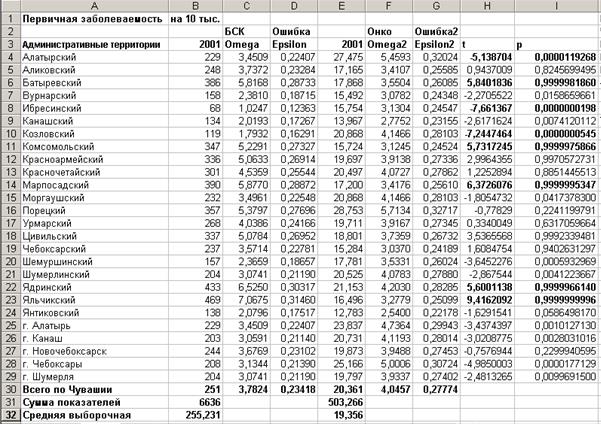
Из табл. 1 видно, что достаточное значение t, равное 5 и более, у 8 районов (Алатырский, Батыревский, Ибресинский, Козловский, Комсомольский, Марпосадский, Ядринский, Яльчикский). Именно эти районы дают большие веса в различии характера возникновения и течения заболеваний (БСК и онкологии) и сильно контрастируют на общем эпидемиологическом фоне с другими районами и даже городами Чувашии. Их суммарный вес составляет более 56,42% в общем эпидемиологическом контрасте (сумма абсолютных значений t).
Выделенным шрифтом отмечены значения показателя заболеваемостей в районах, имеющих сильные контрастные и достоверные различия в характере течения заболевания, и которые являются основой для перестроения всех остальных показателей в других районах.
В соответствии с табл. 1 сформируем исходные данные в табл. 2 для формирования множества векторов ненатурального равномерного двоичного кода G длины n с ошибкой кратности t, определенным количеством информационных разрядов k, расстоянием в смысле Хэмминга dmin, описывающие характер БСК. Методом наименьших квадратов [4] оценим коэффициенты С1, С2 уравнения спирали 
с учетом критерия максимального приближения к построенным точкам. Запишем значения CS, С1, С2, n, t, k, dmin в виде табл. 2. Определим значение 
=С1×С2 для двух фаз формирования векторов кода G [1].
Таблица 2
Основные параметры алгоритма построения образа обратного развития заболевания БСК организма человека и его представление по двум разнохарактерным группам исследования на основе построения множества двоичных векторов
|
Административная территория |
C |
С1 |
С2 |
n |
t |
k |
dmin |
|
Алатырский район |
-14,45 |
-0,994 |
14,533 |
35 |
5 |
15 |
8 |
|
Батыревский район |
-1,85 |
-0,118 |
15,614 |
58 |
6 |
34 |
8 |
|
Ибресинский район |
1,99 |
0,239 |
8,333 |
20 |
8 |
4 |
8 |
|
Козловский район |
-2,31 |
-0,239 |
9,667 |
20 |
7 |
4 |
8 |
|
Комсомольский район |
30,22 |
-1,194 |
25,300 |
52 |
6 |
4 |
8 |
|
Марпосадский район |
15,37 |
0,764 |
20,109 |
59 |
6 |
11 |
8 |
|
Ядринский район |
8,95 |
0,431 |
20,743 |
65 |
6 |
17 |
8 |
|
Яльчикский район |
17,64 |
0,852 |
20,690 |
71 |
9 |
35 |
8 |
В табл. 2 представлены параметры сгенерированных фаз состояния процесса неразвития и характера течения заболеваний БСК на 8 административных территориях.
Для генерации ненатурального двоичного кода можно использовать разные схемы. Самой распространенной является выборка векторов искомого кода G из линейного группового кода (ЛГК) [7]. И в этом случае также возможны разные алгоритмы подбора подходящих массивов векторов. Мы использовали автоматизированный прием выборки ненатурального кода из ЛГК, порождаемого матрицей на основе программы, разработанной профессором кафедры технологии роботизированного производства Чувашского госуниверситета Ивановым А.Г. [2] Особенностью этой программы является универсальность алгоритма генерации двоичных векторов в диапазоне n = 20… 100, t = 1…10, dmin = 4…10. Требуется подготовить данные таким образом, чтобы они попали в этот диапазон. Можно рекомендовать использовать другие алгоритмы генерации, например используя циклические коды [7].
Рассмотрим сеанс работы программы generic.exe при генерации векторов ненатурального двоичного кода G, размещаемых на фазовой плоскости в полярной системе отсчета, описывающего характер болезней систем кровообращения (БСК) с параметрами, записанными в табл. 2.
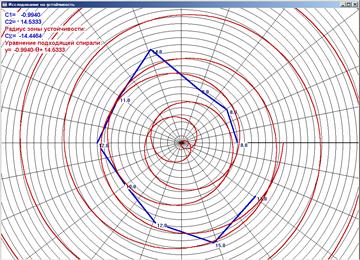
Рис. 1. Сеанс работы программы spiral.exe при генерации метрического пространства на основе спиралей на фазовой плоскости в полярной системе отсчета, описывающего характер БСК по Алатырскому району
Отобразим точки в полярной системе отсчета (рис. 1), соответствующие искаженным векторам кода, радиус ρ = dmin, а угол определяется рассеянием точек в диапазоне q = 0…2π. Отобразим все фазы для построения образа на лепестковой диаграмме (рис. 2). Далее рассмотрим образ обратного развития заболевания БСК человека и его представление в виде лепестковой формы, отклоняющейся к центру в область отрицательных, соответствующих устойчивому характеру стабильного, корневого, здорового состояния организма, представленный на рис. 2. Величина и сила отклонения лепестка и его привязка к административным региональным влияниям четко просматривается на рисунке. Алатырский район, имеющий устойчивый синдром к БСК, создает контрасты с группой районов, менее устойчивых к заболеваниям БСК (Батыревский, Ибресинский, Козловский), нейтральных к корневому влиянию на развитие более устойчивой ситуации. Но контраст устойчивого, стабильного развития ситуации, обратного развития заболеваний вдвое меньше деструктивного контраста Комсомольского группового фактора и равен по весу деструктивному контрасту в Яльчикском, Ядринском и Мариинско-Посадском районах.
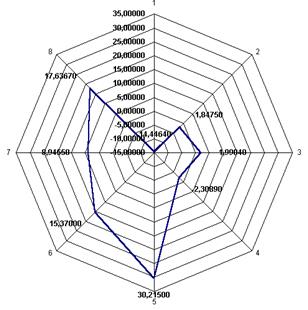
Рис. 2. Образ обратного развития заболевания (БСК) человека и его представление в виде лепестковой формы, отклоняющейся к центру в область отрицательных, соответствующих устойчивому характеру стабильного, корневого, здорового состояния организма
Выводы
1. Анализируя образ обратного развития заболевания (болезней систем кровообращения) человека и его представление в виде лепестковой формы, можно отметить сценарий сворачивания всех негативных, растущих в положительную сторону лепестков. Это сценарий обратного развития заболевания. Он соответствует искоренению различий, контрастов в процессах разнохарактерных (по разным нозологиям заболеваний) групп исследования. Математически надо создать условия для выборочного уменьшения значений t (равные 5 и более), которые достоверны и достаточны для контрастного геометрического построения образа лепестка. Практически – выполнить мероприятия, медико-организационные меры, разрешающие отличия в разнохарактерных группах больных. Уменьшение размеров лепестков будет соответствовать оздоровлению ситуации в районах и в целом в регионе. Фазовое приближение к центру, в область нуля и отрицательных значений – характерно описывает образ обратного развития заболевания человека.
2. Отклонение формы, определяющей образ обратного развития заболевания человека и его представление в виде лепестковой формы, к центру, в область отрицательных значений соответствует устойчивому характеру стабильного, корневого, здорового состояния организма.
Рецензенты:
Алексеев Григорий Алексеевич, доктор медицинских наук, профессор кафедры общественного здоровья и здравоохранения АУ Чувашии «Институт усовершенствования врачей» Минздравсоцразвития Чувашии, г. Чебоксары.
Денисова Тамара Геннадьевна, доктор медицинских наук, доцент, проректор по научной работе и международным связям АУ Чувашии Чувашской Республики «Институт усовершенствования врачей» Минздравсоцразвития Чувашии, г. Чебоксары.
Библиографическая ссылка
Шувалова Н.В., ИВАНОВ А.Г., Герасимова Л.И., ТЮРНИКОВА С.Р. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ПОСТРОЕНИЯ ОБРАЗА ОБРАТНОГО РАЗВИТИЯ БОЛЕЗНЕЙ СИСТЕМЫ КРОВООБРАЩЕНИЯ НА ТЕРРИТОРИИ ЧУВАШСКОЙ РЕСПУБЛИКИ // Современные проблемы науки и образования. – 2013. – № 3. ;URL: https://science-education.ru/ru/article/view?id=9149 (дата обращения: 19.04.2024).