Для получения достоверных данных при проведении лабораторных испытаний необходимо обеспечить идентичность процессов на фрикционном контакте реального сопряжения с процессами на модели.
В качестве модели использовалась пара трения «колодка-ролик», устанавливаемая на машину трения СМТ-1. Одной из наиболее распространённых задач физического моделирования является расчёт масштабного фактора, определяющего количественную связь между режимами работы реального сопряжения и модели в зависимости от геометрических размеров контактирующих элементов трибосистемы.
Основными условиями идентичности процессов в реальном сопряжении и в моделируемой паре трения будут соблюдение реальных температур и равенство контурных давлений в трибоконтакте [3]. По данным исследований [2], температура поверхности трения поршневого пальца и втулки шатуна двигателя КамАЗ-740 находится в пределах Тср=180.
Тепловыделение в трибоконтакте зависит от режима работы сопряжения и определяется по формуле:
, (1)
где R – количество теплоты, выделившееся на контакте в единицу времени, Вт; Vск – скорость скольжения, м/с; fтр – коэффициент трения, при граничном трении fтр=0,1.
Количество теплоты, отведённое от сопряжения, можно определить по формуле Ньютона [4]:
, (2)
где Q – количество теплоты, отведённое от ролика в результате конвективного теплообмена, Вт; α – коэффициент теплоотдачи, Вт/(м2∙град); F – площадь поверхности ролика, м2; Т1 – температура поверхности ролика, °К; Т2 – температура окружающего воздуха, °К.
Добиться идентичности температурных характеристик реального сопряжения и моделируемой трибопары можно путём решения уравнения теплового баланса относительно нагрузки N=Nкр.т., которая будет являться верхним пределом возможного диапазона нагружения моделируемой трибопары:
, (3)
где Nкр.т. – нагрузка, обеспечивающая в моделируемом сопряжении верхний критический предел температуры реального сопряжения Т1=Ткр., Н.
Коэффициент теплоотдачи можно определить из критериального уравнения, составленного для случая отдачи тепла стенками труб при поперечном обдуве воздухом [4]:
, (4)
где Nu – критерий Нуссельта; Re – критерий Рейнольдса; с, n – коэффициенты, определяемые экспериментальным путём.
Подставив значения критериев Нуссельта и Рейнольдса в уравнение, можно получить значение коэффициента теплоотдачи:
, (5)
где λ – коэффициент теплопроводности воздуха, λ=2,59∙10-2 Вт/м∙К; d – диаметр ролика, м; υ – кинематическая вязкость воздуха, υ=15,06∙10-6 м2/с.
Определить коэффициенты c и n можно, выразив α из уравнения (2) и подставив его в критериальное уравнение (4):
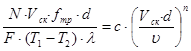. (6)
Прологарифмировав данное уравнение, можно представить его в виде степенного полинома:
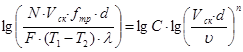. (7)
Подставляя экспериментальные значения переменных в уравнение (7) и аппроксимируя результаты по методу наименьших квадратов, находим значение коэффициентов, и, поставив (5) в (3), окончательно получим:
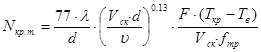, (8)
где Tкр – температура в зоне бобышек поршня при работе двигателя КамАЗ-740 на режиме номинальной мощности, °К; Тв – температура окружающего воздуха, °К.
Поверхность охлаждения ролика определяется по формуле:
, (9)
где d – диаметр ролика, м; b – ширина ролика, м.
Вторым необходимым условием достижения идентичности условий трения в сопряжении и моделируемой паре является равенство напряженных состояний трибоконтакта [1], которое при прочих равных условиях определяется равенством контурных давлений [3; 5].
Для подшипников скольжения для расчётов контурных давлений можно использовать формулу:
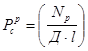, (10)
где 
– контурное давление в реальном сопряжении, Па; Np – нормальная нагрузка на подшипники, Н; Д – диаметр поршневого пальца, м; l – длина втулки, м.
Для моделируемой пары трения (типа «колодка-ролик») после тщательной обработки контурная площадь будет соответствовать номинальной, а давление будет определяться по формуле:
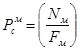, (11)
где 
– контурное давление в моделируемой паре трения, Па; Nм – усилие прижатия колодки к поверхности ролика, Н; Fм – площадь контакта моделируемой пары трения, м2.
Усилие прижатия колодки к ролику Nм ограничено с одной стороны (сверху) условием идентичности температурных режимов Nм ≤ Nкр.т, а с другой стороны – техническими возможностями машины трения СМТ-1, Nм ≥ 200 Н.
Таким образом, выполняя условие 200 ≤ Nм ≤ Nкр.т и приравняв уравнения (10) и (11), получим диапазон возможных площадей контакта в моделируемой паре трения:
. (12)
Для выбранной площади контакта моделируемой пары трения пересчёт нагрузок с модели на реальные условия будет производиться по формуле:
. (13)
Скорость скольжения поверхности поршневого пальца относительно втулки верхней головки шатуна имеет сложный характер и зависит как от частоты вращения, так и от угла поворота коленчатого вала двигателя. В связи с этим при моделировании процессов трения принимается средняя скорость скольжения, определяемая по формуле:
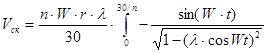, (14)
где Vск – скорость скольжения поршневого пальца, м/c; n – частота вращения коленчатого вала двигателя, об/мин; W – угловая скорость, с-1; r – радиус поршневого пальца, м.
, (15)
где R – радиус кривошипа, м; L – длина шатуна, м.
Результаты расчёта основных параметров моделирования трения в сопряжении «поршневой палец - втулка» на машине трения СМТ-1 приведены в таблице 1.
Таблица 1 – Основные параметры моделирования трения в сопряжении «поршневой палец – втулка» на машине трения СМТ-1
|
Моделируемое сопряжение |
Температура в раб. зоне, Т, °С |
Коэф. трения Н |
Скорость скольжения, Vск, м/с |
Nкр.т, Н |
Nм, Н |
Площадь моделир. трибоконт., мм2 |
Nр, Н |
|
Поршневой палец (сталь 12ХН2) |
180 |
0,1 |
1 |
867 |
800 |
50 |
29,6∙Nм |
|
Втулка ВГШ (Бр ОС10-10) |
Определение основных размеров колодки производилось с использованием формулы для определения площади трибоконтакта колодки с роликом:
, (16)
где Fкол. – площадь контакта, определённая из условий моделирования, мм2; Д – диаметр ролика, мм; h – ширина колодки, мм; b – длина колодки, мм.
Таким образом, полученные параметры моделирования трения в сопряжении «поршневой палец – втулка» позволяют создать при лабораторных исследованиях максимально приближенные условия процесса трения, происходящие в реальном сопряжении, тем самым свести к минимуму ошибку результатов опытов.
Рецензенты:
Котиков Ю.Г., д.т.н., профессор, преподаватель кафедры «Транспортные системы» ГОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.
Евтюков С.А., д.т.н., профессор, заведующий кафедрой «Наземные транспортно-технологические машины» ГОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.
Библиографическая ссылка
Романов Д.В. ОПРЕДЕЛЕНИЕ УСЛОВИЙ МОДЕЛИРОВАНИЯ ТРИБОТЕХНИЧЕСКИХ ПРОЦЕССОВ СОПРЯЖЕНИЯ ТИПА «ВАЛ – ВТУЛКА» НА МАШИНЕ ТРЕНИЯ СМТ-1 // Современные проблемы науки и образования. – 2013. – № 2. ;URL: https://science-education.ru/ru/article/view?id=9138 (дата обращения: 01.12.2023).