Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бараков В.С. 1

---

1 ФГБОУ ВПО «Волгоградский государственный университет»

В статье рассмотрены подходы к построению многофакторной оценки результативности модернизационных преобразований, позволяющие проанализировать взаимосвязь исследуемых факторов и прогнозировать развитие исследуемого объекта. Смоделирована эконометрическая модель многофакторной оценки влияния различных факторов на сальдированный финансовый результат в расчете на 1 руб. инвестиций в основной капитал, основанная на применении корреляционного и регрессионного анализа. Проводится поэтапный регрессионный анализ оценки результативного показателя «сальдированный финансовый результат в расчете на 1 руб. инвестиций в основной капитал» по всем макрорегионам РФ за период с 2000 по 2011 г., включающий: отбор показателей, корреляционный анализ их взаимозависимости, проверка значимости, как отдельных коэффициентов, так и полученного уравнения множественной регрессии в целом. Сформулирована экономическая интерпретация полученных результатов.

Статья в формате PDF

142 KB

результативность модернизационных преобразований

регрессионный анализ

корреляционный анализ

регион

инвестиции

оценка

экономическое развитие

1. Буянова М. Э. Оценка риска социально-экономического развития регионов Юга России (факторный подход) // Вестник Волгоградского государственного университета. Серия 3. Экономика. Экология // Научно-теоретический журнал. – Волгоград: Изд-во ВолГУ. – № 1(20). – 2012. – С. 85–94.

2. Вуколов Э. А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXCEL: Учебное пособие / Э. А. Вуколов. – М: ФОРУМ: ИНФРА-М, 2004. – С. 160.

3. Дегтярева Т. Д., Буреш О. В., Чепасов В. Статистический анализ транспортного комплекса региона на основе регрессионных моделей / Т. Д. Дегтярева, О. В. Буреш, В. Чепасов // Вопросы статистики. – 2003. – № 8. – С. 65–67.

4. Калинина А. Э., Калинина В. В. Многофакторная оценка состояния промышленности регионов Южного федерального округа (ЮФО) // Современные проблемы науки и образования. – 2012. – № 5.

5. Плышевксий Б. О промышленной политике // Экономист. – 2004. – № 9. – С. 9.

6. Регионы России. Социально-экономические показатели. 2010: Стат. сб. / Росстат.  М. – Режим доступа http://www.gks.ru/bgd/regl/B05_14p/Main.htm.

7. Регионы России. Социально-экономические показатели. 2012: Стат. сб. / Росстат.  М., 2012.  990 с.

8. Читая Г. О. Источники инвестиционного обеспечения экономического развития макрорегионов России // Вопросы статистики. – 2005. – № 9. – С. 34–43.

9. Юзбашев М. М. Расчет объема выборки для надежного установления связи / М. М. Юзбашев // Вопросы статистики. – 2004. – № 6. – С. 38–39.

Введение

Определение потенциала экономического развития регионов является одной из важнейших задач региональной экономики. Данный процесс во многом зависит от инвестиций, которые осуществляются в региональной хозяйственной системе. Для выявления тенденций модернизационных преобразований в России в макрорегиональном срезе возможно применение эконометрических методов анализа [1, 3]. Особый интерес представляет оценка влияния факторов на эффективность инвестиционных процессов в макрорегионе (МР). Решение этой задачи требует определения результирующего показателя, характеризующего эффективность инвестиционных процессов. Здесь речь идет о процессах инвестирования средств в основной капитал.

Результаты и обсуждения

Отношение финансового результата к инвестициям в основной капитал по МР отражает совокупную эффективность инвестиционных процессов. В таком случае получится своего рода обобщающий индикатор, позволяющий оценивать отдачу вложенных в основной капитал средств, а эффект выражается совокупным (сальдированным) финансовым результатом.

В соответствии с методологическими пояснениями российского статистического ведомства «сальдированный финансовый результат (прибыль минус убыток) представляет собой сумму прибыли (убытка) от продажи товаров, продукции (работ, услуг), основных средств, иного имущества организаций и доходов от внереализационных операций, уменьшенных на сумму расходов по этим операциям» [7]. Другими словами, сальдированный финансовый результат регионов и макрорегионов страны, являющийся частью прибавочного продукта, является важным обобщающим показателем их производственно-хозяйственной деятельности. В частности, Б. Плышевский при анализе возможностей самофинансирования инвестиций, в качестве показателя прибыли использует сальдированный финансовый результат [5].

Оценка эффективности инвестиционных процессов в МР, входящих в состав ФО РФ, является актуальной проблемой. Уровень эффективности процессов инвестирования средств в основной капитал является интегральной характеристикой и определяется достаточно большим множеством факторов. Построение такого показателя в рамках детерминированных моделей затруднительно. Наш подход основан на применении линейной модели множественной факторной регрессии. Зависимой, обобщающей переменной мы предлагаем использовать отношение сальдированного финансового результата к объему инвестиций в основной капитал [8].

Многофакторная модель строится в соответствии с функциональной зависимостью типа:

=x1, …, x12, ) , (1)

– сальдированный финансовый результат в расчете на 1 руб. инвестиций в основной капитал, %;

– уровень безработицы (%);

– доля инвестиции в основной капитал организаций с участием иностранного капитала (%);

– уровень экономической активности населения (%);

– индекс промышленного производства (в % к предыдущему году);

– удельный вес убыточных организаций (в % от общего числа организаций);

– степень износа основных фондов, %;

– инвестиции в основной капитал на душу населения (тыс. руб.);

– индекс физического объема инвестиций в основной капитал (в % к предыдущему году);

– удельный вес инвестиций в основной капитал в валовом региональном продукте;

– доля собственных средств в источниках финансирования инвестиций в основной капитал, %;

– доля банковских кредитов в привлеченных источниках финансирования инвестиций в основной капитал, %;

– доля бюджетных средств в привлеченных источниках финансирования инвестиций в основной капитал, %;

– случайная составляющая.

Исходная система данных рассчитана по восьми МР России за 2000–2011 гг. Значения признаков-показателей были отобраны на основе статистических сборников: «Регионы России – 2005», «Регионы России – 2005», «Регионы России – 2010» «Регионы России – 2012» и данных единой межведомственной информационно-статистической системы – http://www.fedstat.ru/indicators/start.do%20%5b46, 7].

Обработка собраной аналитической информации проводится с помощью корреляционного и регрессионного анализа [2]. Корреляция характеризует меру зависимости переменных между собой. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Значение -1.00 означает полностью отрицательную корреляцию, значение +1.00 означает полностью положительную корреляцию. Значение 0.00 означает отсутствие корреляции. Две переменные могут быть связаны таким образом, что при возрастании значений одной из них значения другой убывают. Это и показывает отрицательный коэффициент корреляции. Про такие переменные говорят, что они отрицательно коррелированны.

Связь между двумя переменными может быть следующей,когда значения одной переменной возрастают, значения другой переменной также возрастают. Это и показывает положительный коэффициент корреляции. Про такие переменные говорят, что они положительно коррелированны. Наиболее часто используемый коэффициент корреляции Пирсона r называется также линейной корреляцией, т.к. измеряет степень линейных связей между переменными.

Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными и зависимой переменной. Информация о наличии такой связи может быть использована при анализе множественной регрессии, для построения регрессионного уравнения [3, 9]. Когда определено уравнение регрессии, аналитик может построить график ожидаемого изменения величины зависимой переменной.

Описанный выше метод используется в исследовании для анализа корреляционной зависимости 12 факторов, предположительно влияющих на итоговый показатель – сальдированный финансовый результат в расчете на 1 руб. инвестиций в основной капитал.

Корреляционная матрица независимых факторных признаков показывает, что они слабо коррелируют между собой, и поэтому с применением метода пошаговой регрессии появляется возможность построить значимую модель линейной регрессии (см. табл. 1).

Таблица 1

Корреляционная матрица независимых факторных признаков

Для получения регрессионного уравнения необходимо провести ступенчатый отсев регрессоров. Процесс повторяется до тех пор, пока не останутся только значимые регрессоры.

В результате получено следующее уравнение множественной регрессии следующего вида:

Y=259,2-1,4х5+0,3х7+0,3х8-6,1х9-0,8х10-1,7х11 (2)

Коэффициенты регрессионной модели на заданном уровне значимы.

Статистические оценки модели и ее параметров оказались полностью состоятельными (рис. 1):

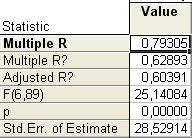
Рис. 1. Параметры оценки регрессионной модели

R – коэффициент множественной корреляции (описывает степень линейной зависимости между Y и факторами);

F- F – статистика;

p – вычисленный уровень значимости модели.

Коэффициент множественной корреляции показывает, что 79,3 % суммарной вариации результирующего показателя объясняется вариабельностью включенных в модель факторов. О неслучайной природе полученных значений коэффициентов регрессии свидетельствуют их стандартные ошибки. В наших расчетах принят 5 %-й ( уровень вероятности ошибки. В модели расчетные значения стандартных ошибок для всех коэффициентов регрессии меньше задаваемого уровня.

Из рис. 1 видно, что статистика критерия Фишера равна F(6,89)=25,14. Так как p=0,0000, что меньше, чем = 0,05, то гипотеза о незначимости модели отклоняется.

На рисунке 2 представлен фрагмент графика остатков:

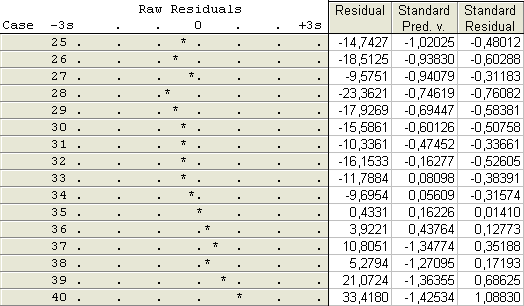
Рис. 2. График остатков

Все остатки укладываются в симметричную относительно нулевой линии полосу шириной ±2S. Это означает, что, по-видимому, дисперсии ошибок наблюдений постоянны.

Из графика видно, что точки расположены близко к прямой, значит, можно предположить, что остатки распределены по нормальному закону. Таким образом, можно считать, что предположения регрессионного анализа выполняются.

Таблица 2.3

Приоритеты факторных признаков по степени их влияния на эффективность инвестиционных процессов в МР России

Таким образом, полученное уравнение множественной регрессии (2) показывает высокую тесноту связи между эффективностью инвестиционных процессов по МР России и выделенными приоритетными признаками-показателями. Об этом свидетельствуют высокое значение коэффициента множественной корреляции, превышающего критический его уровень (0,7), и коэффициент детерминации.

По величине коэффициентов при факторных признаках уравнения регрессии (2) представляется возможным выделить приоритеты изучаемых факторов по степени их влияния на эффективность процессов инвестирования средств в основной капитал. Полученные результаты приведены в табл. 2.3, в которой приоритетность факторов-признаков ранжируется в соответствии со значениями коэффициентов регрессии, позволяющих определить степень их влияния на уровень показателя «финансовый результат / инвестиции в основной капитал», отражающего динамику эффективности инвестиционных процессов в российской экономике в срезе ее крупных макрорегионов, интегрированных в рамках федеральных округов. При этом следует заметить, что приведенное в табл. 2.3 экономическое содержание факторов служит для описания имевших за анализируемую динамику место тенденций в распределении и использовании инвестиций в основной капитал по макрорегионам России.

Заключение

На основе проведенного факторного исследования динамики инвестиций в МР можно сформулировать следующие основные выводы по России:

1. Уравнение линейной множественной регрессии (2), его аналитическое качество, подтверждаемое высоким значением множественного коэффициента корреляции , а также отмеченные выше статистически состоятельные оценки параметров модели показывают, что эффективность процессов инвестирования средств в основной капитал в России имеет высокую тесноту связи с выделенными приоритетными факторными признаками. Кроме того, на основе полученной регрессионной модели выявлен ряд важных тенденций в динамике инвестирования средств в ФО России.

2. На увеличение совокупной чистой прибыли предприятий и организаций России в МР срезе в результате инвестирования средств в основной капитал наибольшее положительное влияние оказывали следующие два фактора:

инвестиции в основной капитал на душу населения (тыс. руб.);

индекс физического объема инвестиций в основной капитал (в % к предыдущему году).

3. На уровень эффективности инвестиционных процессов в России негативное влияние оказывали:

слабая инвестиционная активность банков и собственных средств, выражавшаяся в малой доле долгосрочных инвестиционных кредитов в активных операциях, что в значительной мере было обусловлено ограниченностью долгосрочных пассивов кредитных организаций страны;

большая доля убыточных предприятий и организаций в общей их численности, что существенно снижает эффективность инвестиционных процессов и выражается в снижении суммарного прибавочного продукта.

Рецензенты:

Мосейко В. О., д-р экон. наук, профессор, директор института управления и региональной экономики, ФГАОУ ВПО «Волгоградский государственный университет», г. Волгоград.

Буянова М. Э., д-р экон. наук, профессор кафедры мировой и региональной экономики, ФГАОУ ВПО «Волгоградский государственный университет», г. Волгоград.

Библиографическая ссылка