Введение
Ультразвуковая окорка – это сложный технологический процесс, включающий в себя кавитационный эффект, разрушающий связи между элементами коры, звукокапиллярный эффект и гидродинамические возмущения. Для оценки качества ультразвуковой окорки лесоматериалов, исследования данного процесса осуществляется дифференцированным методом, каждый процесс которого описывается раздельно.
Цель исследования
Целью работы является оценка влияния гидродинамических возмущений, возникающих в жидкой среде, на элементы коры при ультразвуковой окорке лесоматериалов.
Материалы и методы исследования
Задачи построения течения с образованием гравитационных и капиллярных волн на свободной поверхности (поверхности каверны) не имеют принципиальной разницы с задачами для невесомой жидкости. В обоих случаях требуется построить течение, частью ограниченное поверхностями заданной геометрии, а частью – свободными поверхностями, давление на которых постоянно. Форма свободных поверхностей (границ) заранее неизвестна, и определяется в ходе решения задачи из условия постоянства давления [1–5].
Если учесть силы тяжести в формуле Бернулли, то окажется, что скорость на свободной границе не постоянна, а зависит от ординат свободной поверхности:
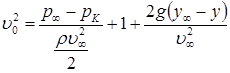 , (1)
, (1)
где ![]() – давление в каверне; g – ускорение свободного падения;
– давление в каверне; g – ускорение свободного падения; ![]() – ордината горизонтальной линии, на которой определяется величина
– ордината горизонтальной линии, на которой определяется величина ![]() в невозмущенном потоке. В формуле (1) скорость на границе каверны, как и ранее, выражена в безразмерном виде, т. е. отнесена к
в невозмущенном потоке. В формуле (1) скорость на границе каверны, как и ранее, выражена в безразмерном виде, т. е. отнесена к![]() .
.
Если свободная граница искривлена, как у естественной формы коры, то на ней возникнут капиллярные силы, величина которых пропорциональна кривизне. Они направлены внутрь каверны, если её граница обращена выпуклостью в сторону жидкости, и наоборот. Обусловленная капиллярностью величина давления:
![]() , (2)
, (2)
где ![]() – кривизна поверхности каверны.
– кривизна поверхности каверны.
Условия (1) и (2) нетрудно учесть при составлении интегральных уравнений кавитационной задачи, которые, естественно, окажутся сложнее уравнений невесомой жидкости. Кроме того здесь возникнут дополнительные трудности в связи с отсутствием гладких решений в окрестности точек сопряжения свободных границ с твердыми поверхностями [5].
При формировании кавитационного течения для разрушения слоёв коры и гидродинамических возмущений на свободной поверхности жидкости образуются гравитационные волны.
Рассмотрим плоское потенциальное установившееся обтекание поступательным потоком безграничной несжимаемой идеальной жидкости удлиненного контура, изображенного на рис. 1, имитирующей окариваемый лесоматериал в технологическом желобе.
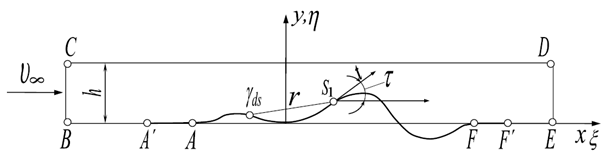
Рис. 1. Схема обтекания удлиненного контура
Часть этого контура ABCDEF соответствует сечению твердых стенок, a AF – сечению свободной поверхности, над которой внутри замкнутого объема, ограниченного твердыми стенками и этой поверхностью, заключен под определенным давлением газ. Такое течение представляет собою типичный пример так называемого искусственного кавитационного течения.
Свободная поверхность, вообще говоря, будет возмущена вследствие влияния на нее обтекания оконечностейСВ и DE. При этом порядок скоростей возмущения на достаточном удалении от указанных оконечностей будет таким же, как от плоских источника и стока, расположенных вблизи СВ и DE, интенсивность которых пропорциональна произведению ширины контура h на модуль скорости невозмущенного потока. Другой причиной возмущений может быть давление газа внутри упомянутого выше объема, заключенного между твердыми стенками и свободной поверхностью (поверхностью коры), если оно будет отличаться от статического давления в невозмущенном потоке на уровне оси х (см. рис. 1).
Обтекание контура коры окариваемого лесоматериала заменяется обтеканием вихрей, распределенных непрерывным образом на твердых стенках и свободной поверхности. Поскольку контур замкнут, величина вихревой интенсивности в его произвольной точке равна модулю скорости в этой точке. Используя условие непроницаемости твердых стенок и свободной поверхности, заключающееся во взаимной компенсации нормальных составляющих скоростей в любой точке контура, обусловленных индукцией вихрей, невозмущенным набегающим потоком и наличием в потоке каких-либо источников возмущений, можно написать интегральное уравнение, дающее связь между формой контура и интенсивностью вихревого:
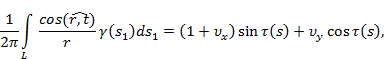 (1а)
(1а)
где![]() – угол между направлением указанной касательной к контуру и отрезком r (см. рис. 1); r – расстояние от точки S1, в которой расположен вихрь
– угол между направлением указанной касательной к контуру и отрезком r (см. рис. 1); r – расстояние от точки S1, в которой расположен вихрь![]() ds1, до произвольной точки s, лежащей на контуре;
ds1, до произвольной точки s, лежащей на контуре;![]() ,
, ![]() – проекции на оси декартовых координат скоростей возмущения в точке s, вызванных каким-либо источником возмущения (например, вихрем, источником, телом, частично или полностью погруженным под свободную поверхность и т. п.);
– проекции на оси декартовых координат скоростей возмущения в точке s, вызванных каким-либо источником возмущения (например, вихрем, источником, телом, частично или полностью погруженным под свободную поверхность и т. п.);![]() угол между вектором скорости набегающего потока и касательной к контуру в точкеs. Интегрирование производится по контуру сечения твердых стенок и свободной поверхности, а все величины, имеющие размерность скорости, отнесены к
угол между вектором скорости набегающего потока и касательной к контуру в точкеs. Интегрирование производится по контуру сечения твердых стенок и свободной поверхности, а все величины, имеющие размерность скорости, отнесены к ![]() .
.
Пределы интегрирования разбиваются на промежутки АА', А'В, ВС, CD,DE, EF',F'F и FA и производится оценка отдельных интегралов по этим промежуткам для значений s, соответствующих точкам свободной поверхности и участкам твердых стенок А'А и FF'.
При оценке интеграла поCD, на этом участке контура можно положить ![]() поскольку вихревая интенсивность равна модулю скорости, а скорость на верхней стороне плоской бесконечно тонкой пластинки равна
поскольку вихревая интенсивность равна модулю скорости, а скорость на верхней стороне плоской бесконечно тонкой пластинки равна ![]() , за исключением малых окрестностей вблизи точек С и D:
, за исключением малых окрестностей вблизи точек С и D:
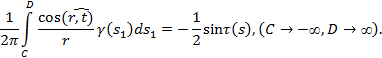 (2а)
(2а)
Используя теорему Бернулли и условие постоянства давления на свободной поверхности, вихревую интенсивность можно выразить через значения ординат свободной поверхности:
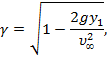 (3)
(3)
где![]() – ускорение свободного падения.
– ускорение свободного падения.
После подстановки и преобразования в соответствии с заданными условиями получается интегро-дифференциальное уравнение для определения формы свободной поверхности воды. При отсутствии возмущений ![]() одним из решений является
одним из решений является ![]() , которое соответствует горизонтальной невозмущенной поверхности.
, которое соответствует горизонтальной невозмущенной поверхности.
Ниже получены интегральные зависимости, исходя из условия равенства нулю суммарной нормальной составляющей скорости в точках свободной поверхности и сечения твердых стенок и из условия равенства вихревой интенсивности в произвольной точке контура значению касательной составляющей скорости к контуру в этой точке.
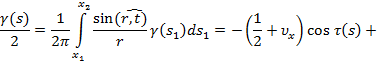
![]() (4)
(4)
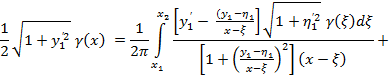
![]() (5)
(5)
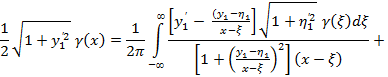
![]() (6)
(6)
Уравнения типа (4) обычно получают иным путем, не рассматривая обтекание замкнутого контура со свободной границей (каверной) на нижней стороне, например, так, как это сделано в работе [7]. Вихревой слой при этом располагают на линии, соответствующей свободной поверхности. Из условия непроницаемости свободной поверхности получают интегро-дифференциальное уравнение, отличающееся формально от соотношения (4) только величиной численного коэффициента, стоящего в правой его части при ![]() (единица вместо
(единица вместо ![]() ). Однако поскольку линия свободной поверхности представляет собою контур незамкнутый, вихревая интенсивность уже не будет равна модулю скорости, а, следовательно, не имеет места такая простая связь между вихревой интенсивностью и формой свободной поверхности, какая дается формулой (5). В этом случае для определения
). Однако поскольку линия свободной поверхности представляет собою контур незамкнутый, вихревая интенсивность уже не будет равна модулю скорости, а, следовательно, не имеет места такая простая связь между вихревой интенсивностью и формой свободной поверхности, какая дается формулой (5). В этом случае для определения![]() (х) необходимо дополнительное нелинейное интегральное соотношение, в которое входит интеграл такого же типа, что и интеграл, стоящий в правой части уравнения (6). Таким образом, вместо простого алгебраического уравнения (5) получают нелинейное интегральное уравнение. В такой постановке задача существенно усложняется и сводится к решению системы, состоящей из упомянутого интегрального уравнения и интегро-дифференциального уравнения типа (4).
(х) необходимо дополнительное нелинейное интегральное соотношение, в которое входит интеграл такого же типа, что и интеграл, стоящий в правой части уравнения (6). Таким образом, вместо простого алгебраического уравнения (5) получают нелинейное интегральное уравнение. В такой постановке задача существенно усложняется и сводится к решению системы, состоящей из упомянутого интегрального уравнения и интегро-дифференциального уравнения типа (4).
Формирование гидродинамической волны, разрушающей элементы коры, определяется конечной амплитудой как на свободной поверхности жидкости, в которой находится окариваемый лесоматериал, так и у границы коры.
Путем элементарных вычислений легко можно получить зависимости теории волн конечной амплитуды. Если положить в формуле (4) ![]() ,
, ![]() то получится уравнение, которое может быть использовано для исследования волн конечной амплитуды:
то получится уравнение, которое может быть использовано для исследования волн конечной амплитуды:
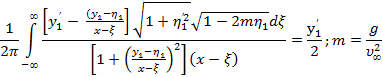 (7)
(7)
Полагая ![]() производя разложение подынтегрального выражения в ряд по степеням
производя разложение подынтегрального выражения в ряд по степеням ![]() подставляя затем в левую и правую части выражения для
подставляя затем в левую и правую части выражения для ![]() в виде ряда:
в виде ряда:
![]() (8)
(8)
и производя элементарные вычисления с использованием формул:
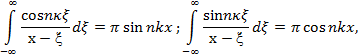
получим в левой и правой частях уравнения (7) ряды по синусам. Сравнение коэффициентов при синусах одинаковых углов позволяет составить систему алгебраических уравнений для определения коэффициентов ![]() ,
, ![]() и т. д. (коэффициент
и т. д. (коэффициент ![]() – величина заданная). Ниже приведена система для вычисления коэффициентов ряда (8), в котором сохранены только три первых члена:
– величина заданная). Ниже приведена система для вычисления коэффициентов ряда (8), в котором сохранены только три первых члена:
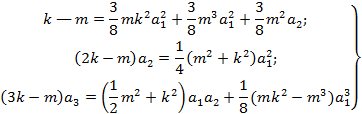 (9)
(9)
где ![]() ; l – длина волны.
; l – длина волны.
Из первого уравнения системы (9) следует, что разность между т и k выражается членами не ниже второго порядка малости отношения амплитуды первой гармоники к длине волны. Значит, с принятой точностью вычислений из второго уравнения следует, что![]() . Тогда из первого уравнения следует что
. Тогда из первого уравнения следует что![]() , откуда можно вычислить зависимость скорости распространения волны от её длины и амплитуды:
, откуда можно вычислить зависимость скорости распространения волны от её длины и амплитуды:
Из третьего уравнения следует, что![]() . Вычисленные данные находятся в согласии с результатами, приведенными в работах [6, 8]. Не представляет принципиальных затруднений и вычисление коэффициентов следующих членов ряда, имеющих более высокий порядок малости. Для волн исчезающе малой амплитуды в формуле (10) можно пренебречь величиной
. Вычисленные данные находятся в согласии с результатами, приведенными в работах [6, 8]. Не представляет принципиальных затруднений и вычисление коэффициентов следующих членов ряда, имеющих более высокий порядок малости. Для волн исчезающе малой амплитуды в формуле (10) можно пренебречь величиной ![]() по сравнению с единицей и получить известное выражение линейной теории волн, связывающее скорость распространения волны с ее длиной.
по сравнению с единицей и получить известное выражение линейной теории волн, связывающее скорость распространения волны с ее длиной.
Заключение
Математическое описание гидродинамических возмущений, возникающих при ультразвуковой окорке в водной среде, дает возможность определить наиболее оптимальные режимы работы технологического комплекса в целом и разработать комплекс рекомендаций при реализации процесса.
Рецензенты:
Иванов Виктор Александрович, д-р техн. наук, профессор, заведующий кафедрой «Лесные машины и оборудование» ФГБОУ ВПО «Братский государственный университет», г. Братск.
Мамаев Леонид Алексеевич, д-р техн. наук, профессор, проректор по учебной работе ФГБОУ ВПО «Братский государственный университет», г. Братск.
Библиографическая ссылка
Гаспарян Г.Д. МОДЕЛИРОВАНИЕ ГИДРОДИНАМИЧЕСКОГО ДАВЛЕНИЯ, ИНИЦИИРОВАННОГО ИЗЛУЧАТЕЛЕМ ПРИ УЛЬТРАЗВУКОВОЙ ОКОРКЕ ЛЕСОМАТЕРИАЛОВ // Современные проблемы науки и образования. 2013. № 3. ;URL: https://science-education.ru/ru/article/view?id=8959 (дата обращения: 22.02.2026).



