Практические задачи управления многими промышленными механизмами предполагают регулирование скорости и положения исполнительного механизма, соединенного с электроприводом через упругую кинематическую передачу, содержащую зазор. К такого рода объектам управления относят опорно-поворотные устройства различного назначения, металлообрабатывающие станки, механизмы металлургического производства и т.п. Системы регулирования для них рационально строить по принципу электромеханической выборки зазора на основе реверсивных многодвигательных электроприводов, с индивидуальными силовыми преобразователями, с учетом упругих механических передач от электродвигателей к общей массе.
К числу основных требований, предъявляемых к указанным электроприводам, относятся высокие показатели надежности работы, а также точности и быстродействия при управлении движением общей массы [1].
Известны способы управления двухдвигательным электроприводом с зазорами в кинематических передачах по принципам электромеханического торсиона (распора), как указано в литературе [2–4], и подчиненного регулирования координат (тока и скорости), основанные на раздельном формировании управляющих воздействий на каждый электродвигатель, в зависимости от разности заданного и действительного значений скорости общей массы, применении корректирующих воздействий на электродвигатели по сумме их скоростей таким образом, что в определенном диапазоне скоростей и моментов нагрузки общей массы электродвигатели развивают моменты разного знака (направления), исключая тем самым влияние зазоров на динамику системы, а за пределами этого диапазона работают в тандеме, развивая одинаковые по величине и знаку моменты и обеспечивая тем самым максимальную перегрузочную способность объединенного электропривода [1].
Математическое описание трехмассового объекта радиотелескопа включает в себя: инерционность первой массы – двигателя; упругая механическая связь с зазором между первой и второй массой; инерционность второй массы – платформы; упругая механическая связь между второй и третей массой; инерционность третьей массы – главного зеркала [2].
На рисунке 1 показана общая структурная схема объекта с регулятором скоростью, где управление по контуру скорости включает в себя модальный регулятор и адаптивное управление с эталонной моделью.
Для радиотелескопа характерно наличие таких внешних и внутренних возмущений как влияние зазора, упругости и ветра, из-за которых возникают колебательные процессы в электрической и механической частях электропривода, что приводит к их повышенному износу, снижению надежности системы и ухудшению качества управления движением рабочего органа. При этом в системах упругие звенья в кинематических передачах приводят к еще более значительному ухудшению показателей качества и надежности работы САУ.
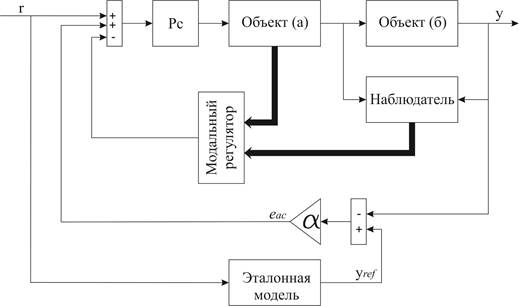
Рис. 1. Структурная схема системы управления радиотелескопа с модально-адаптивным регулятором
Составленные дифференциальные уравнения объекта:
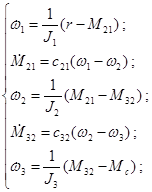
Исходя дифференциальных уравнений, составляется векторно-матричное описание радиотелескопа:
,
,
,
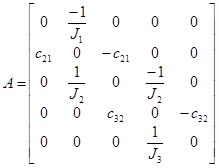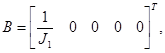
где x – [ω1 M21ω2 M32 ω3].
Для расчета модального регулятора объект управления разбивается на две части:
– объект (а) с непосредственными обратными связями, поскольку скорости двигателя ω1 и платформы ω2 и момент упругости М21 измеряются датчиками (см. рисунок 2 (а)).
– объект (б) с обратными связями по идентифицированным переменам от наблюдателя (см. рисунок 2 (б)). По всем, таким образом, полученным обратным связям рассчитывается модальный регулятор для управления объектом пятого порядка.
Для определения коэффициентов модального регулятора принято распределение корней характеристического уравнения по стандартной форме Баттерворта [3], доставляющего минимум интеграла от квадрата ошибки. Среднегеометрический корень для трехмассовой модели равен w0=24с-1.
При расчетах модального регулятора на основе трехмассовой модели использованы матрицы пятого порядка. Расчеты выполнены по команде PLACE – «Желаемое размещение полюсов системы», MATLAB. Кроме того, в регулятор контура скорости, замкнутого по скоростям двигателя и второй и третьей масс, добавлен коэффициент [4]:
kp.c=k1+k2+k3 = 70.4 + 131.685 + 10.834 = 212.919,
а коэффициенты обратных связей модального регулятора по скоростям поделены на этот коэффициент, т.е. определяются какki’=ki/kp.c при i= 1, 3, 5. С учетом сказанного получены значения коэффициентов модального регулятора для трехмассовой модели:
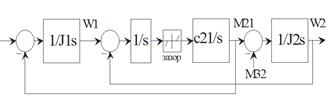
а) объект а – включает в себя: двигатель – J1; платформа – J2; коэффициент упругости механической связи – c21; зазор
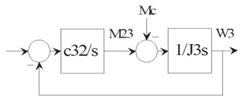
б) объект б – включает в себя: главное зеркало – J3; коэффициент упругости механической связи – c32; возмущение ветра – Mc
Рис. 2
Поскольку наблюдатель построен по описанию объекта (б), уравнения наблюдателя будут иметь следующий вид:
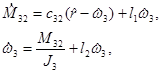где rˆ =ω2,
, 
,
, ,
,
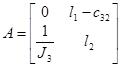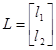где L – коэффициенты наблюдателя, значения коэффициентов при ω0=100с-1таковы
.
Такой подход в синтезе модального регулятора обеспечивает устранение влияния упругости и зазора [5] на объекте. Таким образом, система наведения радиотелескопа сохраняет качество управления, в случае изменения параметров объекта во времени на 200–300 %.
Для устранения влияния ветра на объект используется адаптивное управление с эталонной моделью [6]. Ошибка между значениями на выходе объекта и эталонной модели поставляется в контур скорости с коэффициентом усиления, см. рисунок 1. Эталонная модель является передаточной функций первого порядка 1/s+1.
Ошибка адаптации равна 
где eac – ошибка на выходе эталонной модель и объект, α – коэффициент усиления, yref – выходной сигнал эталонной модели, y – выходной сигнал объекта.
На рисунке 3 результаты получены в среде MATLAB-SIMULINK, в виде переходных процессов скоростей при задании скорости 5 рад/с, с адаптацией (withMR) и без адаптации (withoutMR). Сигнал возмущения приложен на 10 секунде и составляет 10 % от номинального значения двигателя, т.е. Мс= 0.1·356 =35.6 Н·м.
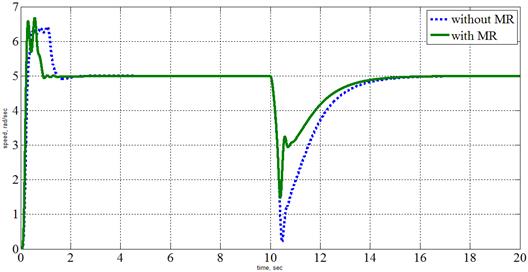
Рис. 3. Переходный процесс скорости главного зеркала при задании 5 рад/с и задания возмущения 35,6 Н.м в 10 секунд
Адаптивное управление обеспечивает больше быстродействия объекту, также система успешно устраняет действие ветра на объекте. Подобный подход даст высокую точность наведения и робастность против различных возмущений или изменения параметров объекта.
Рецензенты:
Поляхов Николай Дмитриевич, доктор технических наук, профессор, «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Зубков Василий Иванович, доктор физико-математических наук, профессор, «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Библиографическая ссылка
Абрахим А.А. УПРАВЛЕНИЕ СКОРОСТЬЮ ТРЁХМАССОВОГО РАДИОТЕЛЕСКОПА НА ОСНОВЕ МОДАЛЬНОГО И АДАПТИВНОГО УПРАВЛЕНИЯ // Современные проблемы науки и образования. 2013. № 2. ;URL: https://science-education.ru/ru/article/view?id=8667 (дата обращения: 09.05.2025).