Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Колесников В.А. 1 Юров В.М. 1

---

1 Карагандинский государственный университет им. Е.А.Букетова

В работе рассмотрены некоторые аспекты метода аналогий, в частности термодинамический, физический и экономический вопросы и их применение к проектированию различных информационно-измерительных систем. Построены наглядные аналогии между термодинамическими, информационно-измерительными и микроэкономическими системами. Получены формулы для оценки эффективности проектирования информационно-измерительных систем, в частности математические выражения, которые можно использовать для выбора процессора при проектировании информационно-измерительных систем и оценить потерю информации. Показано, что объем памяти процессора определяется, в основном, произведением количества информации, поступающей от исследуемого объекта и точности информационно-измерительной системы.

Статья в формате PDF

177 KB

информационно-измерительная система

формула

экономика

физика

термодинамика

метод аналогий

1. Бинс К., Лауренсон П. Анализ и расчет электрических и магнитных полей. – М.: Энергия, 1970. – 376 с

2. Вильсон А. Дж. Энтропийные методы моделирования сложных систем. – М: Наука, 1978. – 246 с.

3. Краузе А., Райхлин Р. Экономика как необратимая (нереверсивная) термодинамическая система // http://finansbibl.ru/bibl/biblioteka/1.htm.

4. Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. – М.: Гостехиздат, 1954. – С. 12.

5. Меркулов В. И. Опыт применения термодинамических методов в экономике // www.cemi.rssi.ru/emm/abst38.htm.

6. Портнов В. С., Юров В. М. Связь магнитной восприимчивости магнетитовых руд с термодинамическими параметрами и содержанием железа // Известия ВУЗов. Горный журнал. – 2004. – № 6. – С. 122–126.

7. Ранеев Г. Г. Измерительные информационные системы. – М: Изд-во МГОУ, 2003. – 536 c.

8. Семёнов В. В. Математическое моделирование динамики транспортных потоков мегаполиса // Препринт ИПМ им. М. В. Келдыша РАН. – М.: 2004. – 32 с.

9. Сергеев В. М. Пределы рациональности. Термодинамический подход к проблеме экономического равновесия. – М: Изд-во Фазис, 1999. – 146 с.

10. Цирлин А. М. Математические модели и оптимальные процессы в макросистемах. – М.: Наука, 2006. – 500 с.

11. Юров В. М., Ещанов А. Н., Портнов В. С, Математические модели электропроводности твердых тел // Материалы III межд. конф. «Математическое моделирование и информационные технологии в образовании и науке». – Алматы, 2005. – Т. 1. – С. 234–237.

12. Яворский В. В., Юров В. М. Прикладные задачи термодинамического анализа неравновесных систем. – М.: Энергоатомиздат, 2008. – 336 с.

Введение

Дж. Максвелл сопоставил созданную им классическую теорию электромагнетизма с гидродинамикой несжимаемых жидкостей и подчеркнул значение такого подхода в науке [7]: В седьмом томе знаменитых фейнмановских лекций по физике глава 12 полностью посвящена электростатическим аналогиям. В настоящее время мы имеем примеры использования физических аналогий для описания процессов различной природы. Так, например, энтропийные модели успешно применяются при анализе процессов миграции населения, обмена и распределения экономических ресурсов и др. [2]. Идеи и методы гидродинамики, нелинейных волновых процессов использовались при построении теории транспортных потоков в больших городах [8]. В [6, 11–12] метод аналогий применялся для анализа процессов в гетерогенных средах. В настоящей работе рассмотрены некоторые вопросы метода аналогий и его применение к информационно-измерительным системам.

Метод аналогий, термодинамика, физика, экономика

В табл. 1 показана аналогия, существующая между величинами в различных скалярных потенциальных полях [1], а в табл. 2 – аналогия между электрическими и акустическими переменными и параметрами [3].

Таблица 1. Аналогия между величинами в потенциальных полях [1]

Таблица 2. Аналогия между электрическими и акустическими переменными и параметрами [3]

В последние годы число работ по использованию методов термодинамики в экономике начало резко возрастать. Как отмечают швейцарские ученые А. Краузе и Р. Райхлин: «Сходство между макроэкономикой и термодинамикой поражает. Перспектива использования достижений термодинамики в исследованиях по экономике представляется многообещающей…» [5]. В работах Меркулова В. И. методы термодинамики применяются к экономическим процессам [9]. В. М. Сергеев публикует монографию: «Пределы рациональности. Термодинамический подход к проблеме экономического равновесия» [10]. Вернемся теперь к методу аналогий. В работе [5] предлагается следующая аналогия между термодинамикой и экономикой (таблица 3).

Таблица 3. Сравнение понятий термодинамики и экономики [5]

В монографии А. М. Цирлина [10] приводится аналогия между термодинамикой и микроэкономической системой (таблица 4).

Таблица 4. Аналогии между термодинамическими и микроэкономическими системами и характеризующими их переменными [10]

Различия между таблицами 3 и 4 связаны: во-первых, с различием между макроэкономической и микроэкономической системами; во-вторых, с различным подходов при выявлении аналогий. А. Краузе и Р. Райхлин исходили в своих рассуждениях из цикла Карно, а А.М. Цирлин – из второго начала термодинамики. Однако, как и в случае аналогии между потенциальными полями (см. таблицу 1), можно провести такую же аналогию и для таблиц 3 и 4 (таблицы 5 и 6).

Таблица 5. Аналогии между термодинамическими и микроэкономическими системами и характеризующими их переменными

Таблица 6. Аналогии между термодинамическими, макроэкономическими и микроэкономическими системами

Используя данные таблиц 1–6, мы можем построить следующую аналогию между полем электрического тока, термодинамикой и микроэкономикой (таблица 7).

Таблица 7. Аналогии между термодинамическими, электрическими и микроэкономическими системами

Метод аналогий и информационно-измерительные системы

Информационно-измерительные системы (ИИС) – это комплекс измерительных устройств, обеспечивающих одновременное получение человеком-оператором или ЭВМ необходимой информации о свойствах и состоянии какого-либо объекта [7]. Структурная схема любой ИИС может быть представлена так, как это показано на рисунке 1. Датчики воспринимают различные параметры объекта измерения, унифицирующие преобразователи унифицируют и передают по каналам связи сигналы датчиков в единый пункт сбора данных. Программное устройство воспринимает информацию датчиков и передаёт её получателю информации. По такой схеме строятся практически все ИИС, включая современные системы передачи информации со спутников и автоматических межпланетных станций.

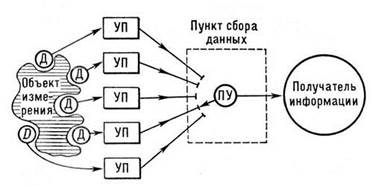
Рисунок 1. Структурная схема информационно-измерительной системы [7]

Построим теперь таблицу аналогий между термодинамикой, ИИС и микроэкономикой (таблица 8).

Таблица 8. Аналогии между термодинамическими, ИИС и микроэкономическими системами

Рассмотрим некоторые примеры использования таблицы 8. Наиболее важным параметром ИИС (да и для любой системы) является ее эффективность η. В термодинамике она соответствует коэффициенту полезного действия тепловой машины:

, (1)

где Тн и Тх – температуры нагревателя и холодильника, соответственно.

Для ИИС уравнение (1) будет выглядеть так:

, (2)

где, согласно таблице 8, Δвх и Δвых – входная и выходная точность ИИС, соответственно. Первая определяется чувствительностью датчика, а вторая – чувствительностью датчика и параметрами унифицирующего преобразователя (рисунок 1). Из формулы (2) следует, что эффективность ИИС в значительной степени определяется структурой и параметрами УП и ПУ (рисунок 1).

Если в качестве функции отклика Ф из [6] взять эффективность ИИС h, то получим:

(3)

где А – работа (энергия), Т – температура, G0 – потенциал Гиббса, m – количество вещества, k – постоянная Больцмана, С – постоянная.

Используя таблицу 8, мы получаем следующее выражение для эффективности ИИС:

(4)

Здесь C1=const. Предельное значение η=1 и из формулы (4) следует:

(5)

Формула (5) определяет правило выбора процессора при проектировании ИИС. Из нее следует, что объем памяти процессора определяется, в основном, произведением количества информации, поступающей от исследуемого объекта и точности ИИС. Последняя, как правило, обратно пропорциональна отношению сигнал / шум и стремится к оптимальному значению при снижении уровня шума. Отметим, что правильный выбор процессора определяет в большей степени стоимость разрабатываемой ИИС. Рассмотрим еще один пример. Вероятность диссипативных процессов в термодинамической системе в большинстве случаев определяется законом Аррениуса:

(6)

где ν=1/τ, τ – время релаксации; Q – энергия активации.

Для ИИС τ – время срабатывания системы, а Q = A = W. С учетом (5), получим:

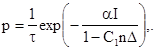(7)

где α – коэффициент размерности.

Из формулы (7) следует, что потеря информации в ИИС тем меньше, чем больше время измерения τ и больше количества информации I от объекта. Необходимо сделать следующее замечание. Действительно, как это следует из (7), замедление переходного процесса (т.е. при увеличении ), вероятность диссипативных процессов уменьшается. Однако на практике такой путь неприемлем, и, наоборот, современные и будущие ИИС должны обладать большим быстродействием для передачи большого массива информации.

В настоящей работе мы стремились показать не только новый подход при анализе проектирования и создания ИИС, но и возможности их разработки, используя полученные выше формулы.

Работа выполнена по программе МОН РК 055 «Научная и / или научно-техническая деятельность», подпрограмма 101 «Грантовое финансирование научных исследований». Контракт № 1932.

Рецензенты:

Портнов Василий Сергеевич, д-р техн. наук, профессор, начальник УМУ, Карагандинский государственный технический университет, г. Караганда.

Турсунбаева Асель Кенжибековна, д-р техн. наук, профессор кафедры ММиН, Карагандинский государственный технический университет, г. Караганда.

Библиографическая ссылка