Введение
Обеспечение предприятий информационными ресурсами обычно сводится к задаче синтеза оптимальных логических структур распределённых баз данных (РБД). Синтез оптимальной логической структуры РБД рассматривается как процесс поиска оптимального варианта отображения канонической структуры РБД в логическую, обеспечивающего оптимальное значение заданного критерия эффективности функционирования корпоративных информационных систем и удовлетворяющего основным системным, сетевым и структурным ограничениями [3, 4]. При отображении канонической структуры в логическую группы данных объединяются в типы логических записей с одновременным распределением их и локальных баз метаданных (ЛБмД) репозитария по узлам ВС. Сложность решения задач синтеза определяется их большой трудоемкостью, связанной с необходимостью учета большого числа параметров и характеристик хранимой в РБД и ЛБмД репозитария информации, запросов и транзакций [3, 4].
Логическая структура РБД и структура размещения БмД репозитария должны обеспечивать сохранение семантических свойств информационных элементов и связей между ними, зафиксированных в канонической структуре РБД с учетом ограничений, накладываемых параметрами СУРБД и локальных СУБД, аппаратных средств передачи данных, топологией ВС и требованиями различных режимов функционирования корпоративных информационных систем.
В качестве одного из основных критериев эффективности используются минимумы: общего времени последовательной обработки множества запросов; транзакций; общего суммарного времени запросов и транзакций. Задачи синтеза оптимальных логических структур РБД и БмД являются нелинейными задачами целочисленного программирования, относящиеся к классу NP-сложных. Разработаны и известны точные и приближённые алгоритмы их численного решения [3,4].
Соответствующие постановки задач оптимизации являются нелинейными задачами целочисленного программирования и включают целевые функции из композиций: линейных форм с бинарными функциями от взвешенных скалярных произведений искомых аргументов; квадратичных форм в сумме с линейными. В работе предложена целевая функция сбалансированной оптимизации по времени выполнения как запросов, так и транзакций. Анализ комбинаторных особенностей сформулированных задач в одном из практически важных частных случаев, проведённый в данной работе, позволил получить их эффективные точные и приближённые аналитические решения, в явном виде как способ прямого заполнения матриц искомых аргументов.
Постановка задач оптимизации
Задача синтеза по критерию минимума общего времени последовательного выполнения множества транзакций формулируется следующим образом [3]:
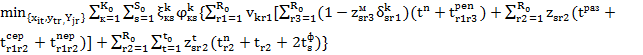 , (1)
, (1)
где переменная ![]() определяет множество узлов-серверов ЛБД, к которым обращается s-транзакция:
определяет множество узлов-серверов ЛБД, к которым обращается s-транзакция:
![]() , если
, если 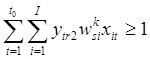 ;
;![]() , если
, если 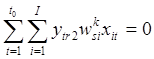 ;
;
переменная ![]() определяет…:
определяет…:
![]() , если
, если 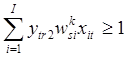 ;
; ![]() , если
, если 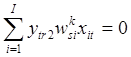 ;
;
переменная ![]() определяет…:
определяет…:
![]() , если
, если 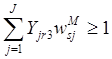 ;
; ![]() , если
, если 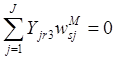 .
.
Аргументами целевой функции (1) являются координаты бинарного вектора, но для удобства трактовки они сгруппированы в 3 бинарных матрицы xit , ytr2 и Yjr3, суть которых следующая: ![]() – включена ли группа данных в логическую запись,
– включена ли группа данных в логическую запись, ![]() – размещена ли логическая запись на сервере узла ВС,
– размещена ли логическая запись на сервере узла ВС, ![]() располагается ли ЛБмД репозитария на сервере узла ВС. Заметим, что целевая функция (1) является композицией линейной формы с бинарными функциями от взвешенных скалярных произведений искомых аргументов.
располагается ли ЛБмД репозитария на сервере узла ВС. Заметим, что целевая функция (1) является композицией линейной формы с бинарными функциями от взвешенных скалярных произведений искомых аргументов.
Для задачи синтеза оптимальной логической структуры РБД на ряде предприятий некоторые технические характеристики, например, временные t можно считать константами [1,2], и вид целевой функции (1) упрощается следующим образом:
![]() , (2)
, (2)
![]() (Yjr3)
(Yjr3)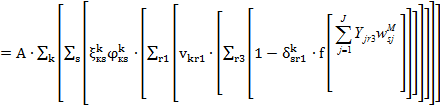 ;
;
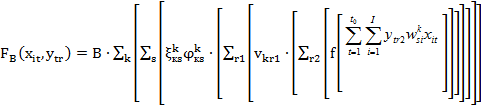 ;
;
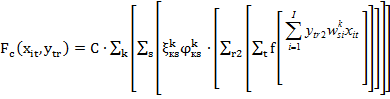 ;
;
где f(x) – бинарная функция ступенчатая функция от взвешенного скалярного произведения соответствующих строк и столбцов матриц аргументов;
![]() ;
; ![]() ;
;![]() – постоянные временные характеристики РБД.
– постоянные временные характеристики РБД.
Полная постановка задачи оптимизации приведена в [3]. В соответствии с принятыми ограничениями в структуре построения ИС, практически важных частных случаев существенными являются только три [1,2]:
В матрице xit в каждой строке только одна 1, остальные 0, что определяет структуру используемых БД.
В матрице xit в каждом столбце не более чем Ft единиц, что определяет ограничение по структуре БД.
В матрице ytr2 в каждой строке не менее одной 1 и не более kкопt штук 1, остальные 0, что определяет необходимое количество копий![]() на используемых вычислительных узлах
на используемых вычислительных узлах ![]() .
.
Тогда решение поставленной задачи будет заключаться в поиске таких матрицxit , ytr2 и Yjr3, при которых целевая функция (2) достигает минимума при указанных ограничениях. Это нелинейная задача целочисленного (бинарного, логического, булевого) программирования, относящаяся к классу NP-сложных.
Задача синтеза по критерию минимума общего времени последовательного выполнения множества запросов имеет следующую целевую функцию [2]:
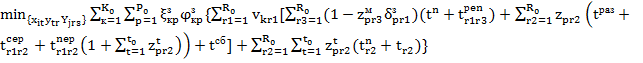 , (3)
, (3)
где переменная ![]() определяет:
определяет:
![]() , если
, если 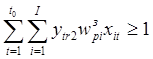 ;
; ![]() , если
, если 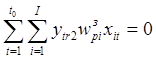 ;
;
переменная ![]() определяет:
определяет:
![]() , если
, если 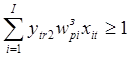 ;
; ![]() , если
, если 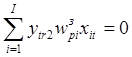 ;
;
переменная ![]() определяет…:
определяет…:
![]() , если
, если 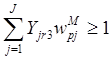 ;
; ![]() , если
, если 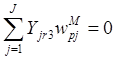 ,
,
при указанных выше ограничениях. Заметим, что целевая функция (3) является композицией квадратичной и линейной форм с бинарными функциями от взвешенных скалярных произведений искомых аргументов.
Аналогично (2), вид целевой функции упрощается:
![]() , (4)
, (4)
![]() (
(![]() )
)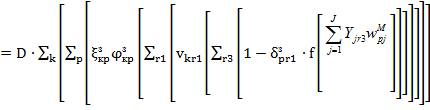 ;
;
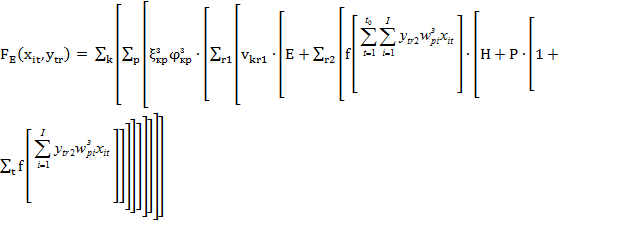 ;
;
FG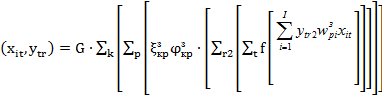 ;
;
где ![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() – постоянные временные характеристики РБД.
– постоянные временные характеристики РБД.
Если необходима оптимизация сразу и по транзакциям, и по запросам, то для задачи синтеза оптимальной логической структуры РБД возможно применение суммы целевых функций (2) и (4):
![]() . (5)
. (5)
Выражение (5) обладает тем недостатком, что слагаемые могут оказаться разного масштаба; соответственно оптимизированным будет либо только время запросов, либо только время транзакций. Для предупреждения этого можно нормировать каждое слагаемое (5):
![]() , (6)
, (6)
где Fmin_z – абсолютный минимум (4), Fmin_tr – абсолютный минимум (2), достигаемые при значениях xit≡0, ytr2≡0 и Yjr3≡1.
Алгоритм аналитического решения.
Общий точный (и приближённый) численный алгоритм решения (методом ветвей и границ) изложен в [3, 4]. Для задач (2) и (4) – а также (5) или (6) – синтеза оптимальной логической структуры РБД, с учётом рассматриваемых ограничений в данном случае, решение может быть получено в явном аналитическом виде как способ прямого заполнения матриц искомых аргументов xit, ytr2 и Yjr3 .Это решение определяется следующими выводами.
1) Целевая функция (2) линейна по переменным zMsr3 , zsr2 и ztsr2 , а целевая функция (4) – и соответственно (5) или (6) – квадратична по переменным zMpr3 , zpr2 и ztpr2 , которые в свою очередь нелинейно определяются независимыми аргументами xit , ytr2 и Yjr3. Ясно, что все zMsr3 и zMpr3, полностью определяемые только Yjr3, для синтеза без ограничений должны быть равны 1, т.к. только они вычитаются, а все остальные добавляются. Это возможно только при матрице Yjr3, все элементы которой 1, что определяет размещение ЛБМд на всех узлах.
2) Для идеальной системы без ограничений все zsr2 и ztsr2, а также все zpr2 и ztpr2, должны быть равны 0. Но это невозможно из-за ограничений, поэтому нулевых должно быть как можно больше. Причём тех, чьи весовые коэффициенты в целевой функции (2) или (4) максимальны.
Таким образом, необходимо обнулить как можно больше zsr2 и ztsr2, zpr2 и ztpr2, это возможно только двумя способами с помощью независимых аргументов xit и ytr2. Первый – с помощью пар произведений xit ∙ ytr2, т.е. как можно меньше должно быть тех индексов t, при которых есть 1 как в xit , так и в ytr2. Ясно, что при заданном Ft таких столбцов с 1 в xit минимум (I = Ft) +1 штук, где I – количество групп данных. Второй – с помощью обнуления скалярного произведения столбцов матриц wksi или wзpi на строки матрицы xit (т.е. выбором ортогональной строки xit), причём тех s или p, которые соответствуют s-му или p-му весовому коэффициенту целевой функции (2) или (4), наибольшему среди остальных. Заметим, что веса попарных произведений в (4) переменных zpr2∙ztpr2 более значимы, чем веса линейных по zpr2 и ztpr2 слагаемых.
3) Если в столбце xit есть хоть одна 1, то в соответствующей строке ytr2 должна быть только одна 1, причём обязательно в одном и том же столбце r2 .
Для переменных zpr2∙ztpr2 , zpr2 и ztpr2 , zsr2 и ztsr2 необходимо учитывать все их весовые коэффициенты. Далее существенно предположение, что расстановка по убыванию весов zpr2∙ztpr2 и ztpr2 одинакова, т.е. можно учитывать только веса, например, ztpr2 , сопоставимые с весами ztsr2.
Таким образом, в данном случае пошаговый алгоритм вычисления оптимального, или по крайней мере приближённо оптимального, решения в явном аналитическом виде как способ прямого заполнения матриц искомых аргументов xit, ytr2 и Yjr3 для целевых функций (2), (4) и (5) или (6) имеет следующий вид.
Шаг 1. а) Для транзакций вычисляются весовые коэффициенты перед переменными ztsr2и zsr2в целевой функции (2):
![]() и
и![]() . (7)
. (7)
в) Для запросов – весовые коэффициенты целевой функции (4) перед переменными zpr2∙ztpr2 , ztsr2 и zpr2 :
![]() и
и ![]() . (8)
. (8)
Шаг 2. Для (2) ранжируются Cs и Bs – с сохранением номера – по убыванию. Если предположение об одинаковости порядков номеров в них не выполнено, то далее можно использовать только Cs, но решение будет приближённо оптимальным из-за высокой степени влияния Сs на значение целевой функции. Для (4), где используется квадратичные зависимости по zi, ранжируются B_Cp , Cp и Bp – с сохранением номера по убыванию. Следует проверить, что предположение об одинаковости порядков номеров в них выполнено – тогда далее можно использовать только B_Cp. Для (5), где используется оптимизация по транзакциям и запросам, ранжируются вместе B_Cp и Cs с сохранением номера p и s – по убыванию. Для (6), где используется нормирование целевых функций, ранжируются вместе B_Cp /2Fmin_z и Cs/2Fmin_tr – с сохранением номера p и s – по убыванию.
Шаг 3. а) Для транзакций из (2) выбирается номер 1-го, т.е. максимального, элемента Cs; (после использования из Cs он удаляется). В матрице wksi выбирается s-тая строка. С_s определяет номер строки, куда переносится единица в заполняемый столбец матрицы решений xit , пока их менее чем Ft, что обеспечивает соблюдение второго ограничения.
в) Для запросов из выражения (4) выбирается номер 1-го, т.е. максимального, элемента B_Cp; (из B_Cp он удаляется после использования).
В матрице wзpi выбирается p-тая строка. B_Cp определяет номер строки, куда переносится 1 в заполняемый столбец матрицы решений xit , пока их менее чем Ft.
с) Для суммарной целевой функции (5) выбирается 1-й, т.е. максимальный, номер B_Cp или Cs. Для (6) это номер B_Cp /2Fmin_z или Cs/2Fmin_tr (из B_Cp или Cs после использования он удаляется). В матрице wзpi или wksi выбирается p-тая или s–я строка. B_Cp или Cs определяет номер p-ой или s-ой строки соответственно, куда заносится единица в заполняемый столбец матрицы решений решения xit , пока их менее чем Ft.
При дублировании 1 или наличии 1 в этой строке уже ранее заполненных столбцов перенос игнорируется. При превышении Ft перенос производится в следующий незаполненный пустой столбец xit (при наличии 1 в этой строке уже ранее заполненных столбцов перенос игнорируется).
Шаг 4. Матрица решения xit заполнена. Матрица решения ytr2 заполняется только одной 1 в каждой из строк, остальные 0. При нулевых столбцах в xit , в соответствующей строке может быть только kкопt единиц; что соответствует ограничению![]() ,где
,где ![]() – максимально допустимое количество копий t-й логической записи.
– максимально допустимое количество копий t-й логической записи.
Шаг 5. Матрица решения Yjr3 заполняется только 1. Здесь не рассматривается ограничение (во многих практически важных случаях несущественное), требующее не более kкопj штук копий j-й ЛБмД в каждой из строк матрицы Yjr3:
![]() , (9)
, (9)
где ![]() – максимальное количество допустимых копий j-й ЛБмД.
– максимальное количество допустимых копий j-й ЛБмД.
Алгоритм заполнения с учётом ограничения (9) требует учёта других весовых коэффициентов переменных при zMsr3 и zMpr3 .
Таким образом, матрицы независимых аргументов xit , ytr2 и Yjr3 заполнены – решение найдено.
Заключение
Результаты, полученные на этапе синтеза оптимальной логической структуры РБД, являются исходными для проектирования физической структуры ЛБмД, а также логических структур локальных и сетевых БД, эффективных сетевых протоколов, обеспечивающих предотвращение взаимоблокировок и появления тупиковых ситуаций при функционировании корпоративных информационных систем.
Результаты решения задач синтеза позволяют определить: состав, структуру, характеристики типов логических записей отношения между ними; размещение типов записей в ВС и использование их процедурами обработки данных; структуру размещения ЛБмД по узлам ВС.
Рассмотрены основные критерии эффективности – минимумы: общего времени последовательной обработки множества запросов; транзакций; общего суммарного времени запросов и транзакций. Предложена целевая функция сбалансированной оптимизации по времени выполнения как запросов, так и транзакций. Анализ комбинаторных особенностей сформулированных задач в одном из практически важных частных случаев, проведённый в данной работе, позволил получить их эффективные точные и приближённые аналитические решения, в явном виде как способ прямого заполнения матриц искомых аргументов.
Список обозначений
![]() – матрица использования групп данных при выполнении запросов;
– матрица использования групп данных при выполнении запросов;
![]() – матрица частот использования запросов пользователями;
– матрица частот использования запросов пользователями;
![]() – матрица использования групп данных при выполнении транзакций;
– матрица использования групп данных при выполнении транзакций;
![]() – матрица частот использования транзакций пользователями;
– матрица частот использования транзакций пользователями;
![]() – матрица прикрепления пользователей к узлам ВС;
– матрица прикрепления пользователей к узлам ВС;
![]() – матрица использования запросов пользователями РБД;
– матрица использования запросов пользователями РБД;
![]() – матрица использования транзакций пользователями РБД;
– матрица использования транзакций пользователями РБД;
![]() – матрица прикрепления запросов к узлам-клиентам;
– матрица прикрепления запросов к узлам-клиентам;
![]() – матрица прикрепления транзакций к узлам-клиентам;
– матрица прикрепления транзакций к узлам-клиентам;
![]() – матрица использования ЛБмД запросами пользователей;
– матрица использования ЛБмД запросами пользователей;
![]() – матрица использования ЛБмД транзакциями пользователей.
– матрица использования ЛБмД транзакциями пользователей.
Рецензенты:
Шевцов Юрий Дмитриевич, доктор технических наук, профессор кафедры информатики и вычислительной техники, ФГБОУ Кубанский государственный технологический университет, г. Краснодар.
Сингаевский Николай Алексеевич, доктор технических наук, профессор, заместитель директора по науке, филиал «Электроазпроект» ДОАО «Электрогаз» ОАО «Газпром», г. Краснодар.
Библиографическая ссылка
Атрощенко В.А., Усатиков С.В., Дьяченко Р.А., Тишковский Д.В. ОПТИМАЛЬНОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ ЗАДАЧ БИНАРНОГО ПРОГРАММИ-РОВАНИЯ ДЛЯ РАСПРЕДЕЛЁННОЙ БАЗЫ ДАННЫХ С ПОСТОЯННЫМИ ВРЕ-МЕННЫМИ ХАРАКТЕРИСТИКАМИ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8565 (дата обращения: 09.03.2026).



