Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Пивень В.В. 1 Уманская О.Л. 1

---

1 ФГБОУ ВПО «Тюменский Государственный нефтегазовый университет»

Для снижения стоимости машины, улучшения ее технических характеристик необходимо оптимальное проектирование конструкций. Оптимальное проектирование позволяет конструкции быть лучшей из всех конструкций данного типа. Первым этапом оптимального проектирования является выбор критерия оптимальности конструкции. Другими словами, это означает выбор целевой функции. Наиболее распространенными целевыми функциями являются следующие: минимум массы; минимум стоимости; минимум веса подкрепляющего или армирующего материала; минимум математического ожидания затрат на конструкцию; минимум суммы стоимости конструкции и затрат на машинное время; принцип одинаковой прочности всех элементов конструкции. При условии однородности конструкции минимум стоимости тождественен минимуму массы. Большинство приведенных критериев будет также соблюдаться при минимуме массы. Масса рамы машины рассматривается как сумма масс составляющих ее элементов. Масса отдельных элементов представлена как функция от площади поперечного сечения и от моментов инерции сечения. Изложенная методика, полученные аналитические зависимости позволят в дальнейшем разработать математическую модель для оптимизации параметров конструкции.

Статья в формате PDF

145 KB

рамная конструкция

сепарирующие машины

целевая функция

оптимизация

математическое моделирование

1. Абгарян К. Л. К теории балок минимального веса. Расчеты на прочность. Вып. 8. – М.: Машгиз, 1962. – 452 с.

2. Анурьев В. И. Справочник конструктора-машиностроителя. Т 1. – М.: Машиностроение, 1982. – 730 с.

3. Виноградов А. И. Проблемы оптимального проектирования в строительной механике. – Харьков: Вища школа, 1970. – 78 с.

4. Куницкий Л. П. Закономерности веса и оптимальная компоновка сплошных изгибаемых металлических элементов // Известия вузов. Строительство и архитектура. – 1965. – № 5. – С. 25-31.

5. Пивень В. В., Уманская О. Л. Определение динамических параметров несущих конструкций вибрационных машин, установленных на упругом основании // Вестник машиностроения. – 2007. – № 5. – С. 14–16.

6. Прагер В. Основы теории оптимального проектирования конструкций: пер. с англ. – М.: Мир, 1977. – 109 с.

7. Рейтман М. И. Методы оптимального проектирования деформируемых тел (постановки и способы решения задач оптимизации параметров элементов конструкций) / М. И. Рейтман, Г. С. Шапиро. – М.: Наука, 1976. – 258 с.

8. Сергеев Н. Д. Проблемы оптимального проектирования конструкций / Н. Д. Сергеев, А. И. Богатырев. – Л.: Стройиздат, 1971. – 135 с.

Введение

При конструировании машин большое значение уделяется созданию машин с оптимальными характеристиками. Вопросам оптимального проектирования конструкций посвящено большое количество научных работ [3, 6, 7, 8]. Под оптимальным проектированием подразумевается такое назначение характеристик конструкции, несущей заданные нагрузки, при котором она в определенном смысле будет наилучшей из всех конструкций рассматриваемого типа. Первым этапом оптимального проектирования является выбор критерия оптимальности конструкции или, иными словами, выбор целевой функции.

Целевая функция является показателем качества конструкции, к оптимизации которого стремятся при ее проектировании. Целевая функция в конечном итоге носит экономический характер и должна иметь практическое значение. Наиболее распространенными целевыми функциями являются следующие [1, 4]: минимум массы; минимум стоимости; минимум веса подкрепляющего или армирующего материала; минимум математического ожидания затрат на конструкцию; минимакс затрат; минимум суммы стоимости конструкции и затрат на машинное время; принцип равнопрочности конструкции.

При условии однородности конструкции минимум стоимости тождественен минимуму массы. Минимум веса подкрепляющего или армирующего материала применяется к армированным бетонным или полимерным конструкциям, в рассматриваемом случае он не актуален. Минимум математического ожидания затрат на конструкцию является аналогом критерия минимальной стоимости, но носит вероятностный характер, как и критерий минимакса затрат. Принцип равнопрочности конструкции аналогичен критерию минимума массы. Следовательно, для рассматриваемой конструкции наиболее подходящим вариантом целевой функции является функция минимума массы.

Уменьшение массы несущей конструкции машины уменьшает металлоемкость конструкции и, как следствие, уменьшение стоимости машин. Снижаются нагрузки на фундамент, что, в свою очередь, оказывает меньшее влияние на протекание технологического процесса.

Во всем многообразии применяемых в промышленности машин проблема снижения массогабаритных характеристик наиболее актуальна для вибрационных сепарирующих машин, применяемых для сепарирования многокомпонентных сыпучих смесей [5]. Особенностью машин данного класса является то, что для осуществления технологического процесса сепарирования рабочим органам машины необходимо задавать вибрационное движение. Это приводит к возникновению значительных динамических нагрузок на детали машины, ее несущую конструкцию, основание, на котором она установлена. Применение уравновешивающих механизмов снижает динамические нагрузки лишь частично. В связи с этим оптимальное проектирование конструкций данных машин является актуальной научной задачей.

Цель исследования: определение целевой функции, позволяющей с помощью математического моделирования спроектировать оптимальную несущую конструкцию вибрационной сепарирующей машины с наименьшими массогабаритными характеристиками.

Материал и методы исследования: в работе использовались теоретические методы исследования, основанные на основных законах механики.

Результаты исследований и их обсуждение

Массу рамы данной машины можно рассматривать как сумму масс, составляющих ее элементов, а именно балок различного профиля. На рис. 1 представлен один из вариантов несущей конструкции. А ниже приведен пример определения массы конструкции из представленных элементов.

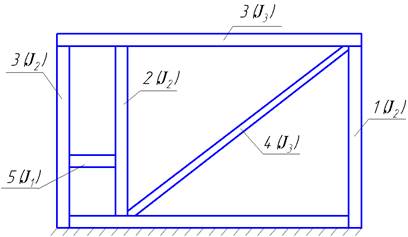
Рисунок 1. Пример схемы несущей конструкции с обозначениями моментов инерции (J) и номерами составляющий балок

Масса каждого стержня может быть представлена формулой:

, (1)

где m – масса стержня, кг; s – площадь поперечного сечения стержня, м2; l – длина стержня, м; – плотность материала, кг/м3.

Массу стержня можно рассматривать как функцию от площади поперечного сечения. Зависимость площади поперечного сечения балок от моментов инерции рассматриваемых балок приведена на рис. 2. Аппроксимация данных графических зависимостей

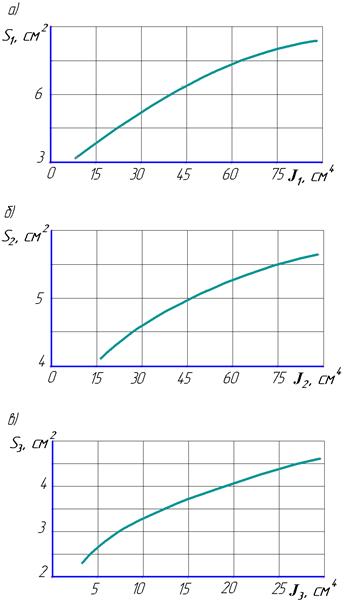
Рисунок 2. Зависимость площади сечения балки (S) от его момента инерции (J): а – для балки № 5; б - для балок № 1, 2 и вертикального участка балки № 3; в – для горизонтального участка балки № 3 и балки № 4

аналитическими выражениями в качестве примера приведена для следующих параметров: длина конструкции L= 2,27 м; высота конструкции H= 1,585 м; длина балки с моментом инерции сечения J1 l1= 0,4 м; J1= 88,35×10-8 м4 (гнутый стальной неравнополочный уголок); J2= 87,88×10-8 м4 (гнутый стальной равнополочный швеллер); J3= 29,96×10-8 м4 (гнутый стальной равнополочный уголок).

Функциональные зависимости площадей поперечного сечения элементов конструкции от их моментов инерции были получены при помощи программы “Maple”:

S1 = -0.7328·J12 + 1.407·J1 + 1.701,

S2 = -0.013·J22 + 0.35·J2 + 3.594 ,

S3 = -0.7328·J12 + 1.407·J1 + 1.701. (2)

Для варианта несущей конструкции из шести балок с тремя различными моментами инерции общую массу конструкции можно представить как сумму масс составляющих ее балок:

m =[ S1 ·l1 + 3S2 ·H + S3 ·(l2 +L)]ρ. (3)

Принимая постоянный профиль балок и используя справочные материалы [2], получаем зависимости масс балок при принятой постоянной длине от моментов инерции сечения (рис.3).

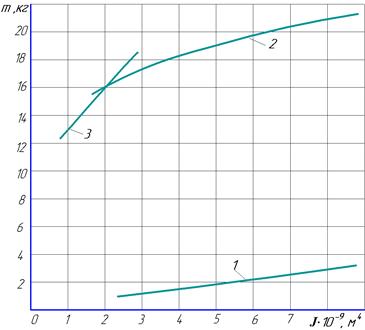
Рисунок 3. Зависимость массы балок (m) от моментов инерции (J): а – для балки № 5; б - для балок № 1, 2 и вертикального участка балки № 3; в – для горизонтального участка балки № 3 и балки № 4

В результате аппроксимации вышеприведенных графических зависимостей при помощи программы “Maple” получены следующие аналитические выражения для определения масс балок:

m1 = -0.0329·10-18 ·J12 + 0.64·J1 ·10-9 - 0.3878,

m2 = -0.049·10-18 ·J22 + 1.3293·J2 ·10-9 + 13.38,

m3 = -0.553·10-18 ·J32 + 5.06·J3 ·10-9 + 8.137. (4)

Общая масса несущей рамной конструкции будет определяться по следующей зависимости:

m = - 0.0329·10-18 ·J12 + 0.64·J1 ·10-9 - 0.049·10-18 ·J22 + 1.3293·J2 ·10-9 –

-0.553·10-18 ·J32 + 5.06·J3 ·10-9 + 21.128 . (5)

Заключение. Изложенная методика, а также полученные аналитические зависимости массы конструкции от составляющих элементов, позволят в дальнейшем разработать математическую модель для оптимизации параметров конструкции.

Рецензенты:

Чумаков В. Г., д-р техн. наук, заведующий кафедрой “Тракторы и сельскохозяйственные машины” Курганской государственной сельскохозяйственной академии имени Т. С. Мальцева Министерства сельского хозяйства РФ, Курганская область, с. Лесниково.

Лапшин И. П., д-р техн. наук, профессор, профессор Государственного аграрного университета Северного Зауралья Министерства сельского хозяйства РФ, г. Тюмень.

Библиографическая ссылка