Введение
Современные тенденции развития бумагоделательной промышленности направлены на увеличение производительности бумагоделательных машин. Это происходит за счет изменения технологических параметров работы машины – увеличения скорости, линейного давления в захвате валов. Увеличение линейного давления в захвате приводит к сокращению срока службы покрытий из-за отслоения полимерного покрытия от металлической рубашки вала.
Одна из важных проблем, стоящих перед производителями покрытий валов, – увеличение адгезии покрытий из полимерных материалов к металлической рубашке вала. Повышения адгезии можно добиться путем совершенствования нескольких факторов: технологии нанесения покрытий (специфическая подготовка поверхности рубашки вала, газотермическая обработка и т.д.), методов расчета напряженно-деформированного состояния (НДС) покрытий с учетом условий их эксплуатации (нагрузки, скорость, температура и т.д.).
Аналитические методы расчета весьма трудоемки и имеют ряд допущений, поэтому не позволяют одновременно учесть несколько факторов: нелинейно-упругое поведение покрытий, нагрузки, температуру. Обладают невысокой точностью расчета. Дорогостоящие комплексные экспериментальные методы занимают много времени для проведения и обработки экспериментальных данных, требуют специальной измерительной аппаратуры и порой не позволяют получить необходимых данных и используются, как правило, для подтверждения результатов численного моделирования. Наиболее полное исследование процессов, протекающих в зоне контакта прессовых валов с полиуретановыми покрытиями, возможно лишь с использованием численных методов расчета, в частности МКЭ, позволяющего учесть сложность геометрии, граничных условий, нагрузок, нелинейные свойства материалов и другие параметры.
В данной статье решается основной подход к исследованию процессов и закономерностей, протекающих в зоне контакта валов с эластомерным покрытием, а также исследование их напряженно-деформированного состояния.
В статье рассматривается имитационное моделирование процессов НДС в зоне контакта валов путем постановки следующих задач:
- определения межосевого расстояния при реальных силовых воздействиях в статике;
- определения нормальных и сдвиговых напряжений в зоне контакта валов;
- исследования напряженно-деформированного состояния в покрытии при изменении его толщины.
Моделирование контакта двух цилиндров с покрытием реализуем в конечно-элементном пакете Ansys (в рамках обучающих лицензий и студенческих версий программ).
Ввиду симметрии модели для сокращения времени расчета и повышения точности результатов целесообразно использовать ¼ часть плоской геометрической модели (рис. 1).
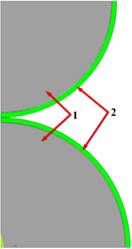
Рис. 1. 2D-модель контакта валов: 1 – валы (сталь 45), 2 – покрытие (полиуретан).
Геометрическая модель служит основой для нанесения регулярной сетки и создания конечно-элементной модели.
Исследуемые покрытия валов представляют собой гиперупругий материал (полиуретан) с нелинейно-упругими свойствами. В первом варианте расчета толщина покрытий составляла 8 мм, во втором 20 мм. Для моделирования таких материалов необходимо выбрать модель поведения материала на основе данных диаграммы «напряжение-деформация», полученной на разрывной машине. В модели используется полиуретан с твердостью 70D, диаграмма «напряжение-деформация» которого показана на рис. 2.
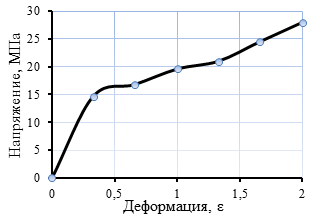
Рис. 2. Диаграмма «напряжение-деформация» полиуретана твердостью 70 ШорD.
Данная модель поведения материала хорошо аппроксимируется моделью Муни-Ривлина с тремя параметрами (рис. 3).
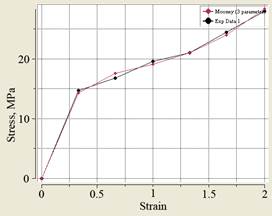
Рис. 3. Аппроксимация экспериментальных данных моделью Муни-Ривлина с 3 параметрами.
Плотность энергии деформации для материала Муни-Ривлина с тремя параметрами имеет вид [4]:
![]() (1)
(1)
где С10 = -8,64·106 МПа, С01 = 2,33·107 МПа, С11 = 1,08·106 МПа – константы материала, характеризующие девиатор деформации материала, ![]() ,
, ![]() – первая и вторая инварианты девиатора деформаций,
– первая и вторая инварианты девиатора деформаций, ![]() ,
, ![]() – параметр сжимаемости материала, J – относительное изменение объема.
– параметр сжимаемости материала, J – относительное изменение объема.
В работе [5] показан тот факт, что сохранение более высокого порядка в модели Муни-Ривлина приводит к лучшей согласованности с экспериментальными данными при большей деформации.
Согласно [1] большинство эластомеров (резиноподобных материалов) характеризуется малой сжимаемостью и изотропией свойств. Материал моделируемого покрытия – полиуретан с коэффициентом Пуассона μ = 0,45.
После построения геометрической модели и определения модели материала следует разбиение площадей рубашки вала и покрытия на подобласти с различными между собой группами признаков. К таким признакам относятся физико-механические свойства материалов, принадлежность подобласти к контактному слою с определенным видом взаимодействия и т.п. Каждая подобласть делится конечным числом четырехугольных элементов, элементы которой образуют регулярную сетку в пределах рассматриваемой подобласти [2]. Эффективность применения МКЭ при решении двух- и трехмерных задач во многом определяется качеством разбиения [3], границы элементов которой должны хорошо аппроксимировать геометрию. Дуги окружностей аппроксимируются ломаными, поэтому плотность сетки контактной подобласти должна быть увеличена для повышения точности расчета.
Задача контакта двух цилиндров, имеющих эластомерные покрытия, относится к классу контактных задач flexible-to-flexible, когда жесткости контактируемых тел близки и происходит деформирование обоих тел. В предположительной зоне контакта валов моделируется симметричный контакт без трения, с использованием 2D-конечных элементов (КЭ) CONTA 175 и TARGE 169 (для контакта типа node-to-surface). На вал и покрытие наносятся элементы PLANE 182 с назначением соответствующего материала. Покрытие крепится к рубашке вала с помощью элементов LINK11 (так как данный элемент характеризует свойства, такие как жесткость сцепления материала). Оба вала имеют соответствующие закрепления: нижний вал закреплен относительно всех степеней свободы. Верхний вал – имеет возможность перемещаться вертикально, относительно оси ОY. К верхнему валу в направлении ОY приложена сила. Конечно-элементная модель валов представлена на рис. 4.
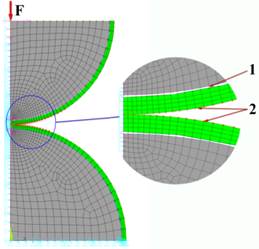
Рис. 4. Конечно-элементная модель валов: 1 – LINK11, 2 – CONTA 175 и TARGE 169.
При решении задачи используем метод внутренних многоточечных ограничений – Multipoint constraint algorithm (или MPC algorithm).
Для расчета используем метод последовательных нагружений с использованием уравнений принципа виртуальных перемещений с начальной базовой конфигурацией [1]:
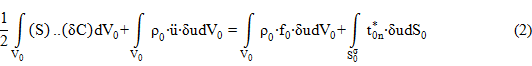
Процесс деформирования представляется как последовательность равновесных состояний, где переход от одного состояния к другому определяется приращением нагрузки. При этом приращение вектора перемещений u при переходе от одного состояния к другому описывается линейными уравнениями. Для каждого шага нагружения вычисляются необходимые меры деформации, по которым рассчитываются необходимые тензоры напряжений.
Результаты численных расчетов для валов с толщиной покрытий 8 мм сведены в таблицу 1, картины распределения напряжений и перемещений представлены на рис. 5.
Таблица 1
Результаты численных расчетов
|
Толщина покрытий, мм |
Усилие прижима F, кН |
Δrрасч, м |
|
|
|
8 |
10 |
0,4·10-3 |
2,4 |
0,5 |
|
15 |
0,64·10-3 |
3,7 |
0,84 |
|
|
20 |
0,86·10-3 |
4,71 |
1,2 |
|
|
25 |
1,1·10-3 |
7,31 |
1,64 |
|
|
30 |
1,42·10-3 |
10,4 |
2,32 |
а) 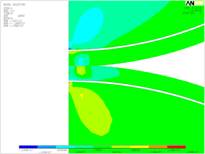 б)
б) 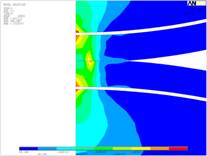 в)
в) 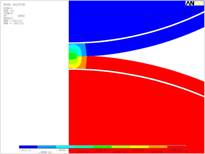
Рис. 5. Характерные картины распределения напряжений и перемещений в покрытии при деформации: а – напряжения сдвига, б – нормальные напряжения, в – перемещения.
Результаты численных расчетов для валов с толщиной покрытий 20 мм сведены в таблицу 2, картины распределения напряжений и перемещения представлены на рис. 6.
Таблица 2
Результаты численных расчетов
|
Толщина покрытий, мм |
Усилие прижима F, кН |
Δrрасч, м |
|
|
|
20 |
10 |
0,33·10-3 |
1,1 |
0,19 |
|
15 |
0,5·10-3 |
1,6 |
0,3 |
|
|
20 |
0,68·10-3 |
2 |
0,42 |
|
|
25 |
0,87·10-3 |
2,6 |
0,55 |
|
|
30 |
0,96·10-3 |
3,1 |
0,71 |
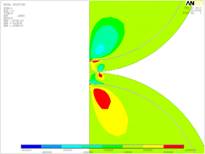
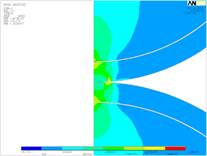
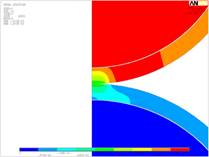
Рис. 6. Характерные картины распределения напряжений и перемещений в покрытии при деформации: а – напряжения сдвига, б – нормальные напряжения, в – перемещения.
Результаты расчетов нормальных напряжений и напряжений сдвига представлены в виде графиков на рисунке 7.
а)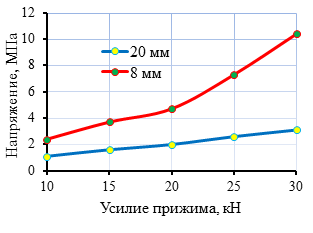 б)
б)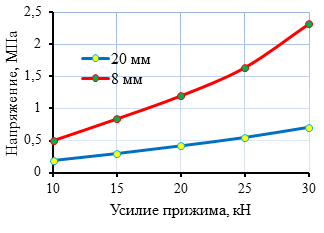
Рис. 7. Графики изменения напряжений: а – нормальные напряжения, б – напряжения сдвига.
В статье приведены количественные и качественные результаты моделирования напряженно-деформированного состояния покрытий. Было установлено, что в зоне контакта на границе «металл-полимер» возникают противоположно направленные сдвиговые напряжения. Если величина сдвиговых напряжений превысит адгезионную прочность соединения «металл-полимер», которая достигает значения порядка 12 МПа, то с большой вероятностью можно утверждать, что может произойти отслоение полимерного покрытия.
Изменение толщины покрытия приводит к изменению напряжений в зоне контакта. Так, при уменьшении толщины покрытия с 20 до 8 мм напряжения в зоне контакта увеличиваются на 60%, что существенно снижает долговечность адгезионного соединения. Но это также приводит к увеличению площадки контакта в захвате.
Данная методика может помочь при выборе свойств полимерных покрытий для работы в конкретных условиях эксплуатации и может быть рекомендована производителям полимерных покрытий.
В дальнейшем планируются исследования напряженного состояния в зоне контакта, зависящего от величины касательных напряжений на поверхности покрытия при передаче момента от одного вала другому.
Рецензенты:
Черемных Николай Николаевич, доктор технических наук, профессор кафедры начертательной геометрии и машиностроительного черчения, УГЛТУ, г. Екатеринбург.
Потехин Борис Алексеевич, доктор технических наук, профессор кафедры технологии металлов, УГЛТУ, г. Екатеринбург.
Библиографическая ссылка
Королев А.В., Санников А.А. ИССЛЕДОВАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ ПОКРЫТИЙ ПРЕССОВЫХ ВАЛОВ БУМАГОДЕЛАТЕЛЬНЫХ МАШИН // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8490 (дата обращения: 09.03.2026).



