Введение
В работе рассматривается задача оптимизации выпуска партии однотипных деталей. Большие партии деталей обычно обрабатываются на конвейерной линии. Задача построения расписаний для конвейера является достаточно простой. Однако в последнее время постоянно меняющаяся номенклатура изделий требует гибкой перенастройки производственной линии, что достигается за счет использования дорогостоящих многофункциональных рабочих станций. Требование загрузки такого универсального оборудования приводит к тому, что на одних и тех же машинах выполняются различные операции технологической последовательности и возникают задачи обработки деталей со сложным технологическим маршрутом.
Постановка выглядит следующим образом. На производственной линии, состоящей из ![]() различных машин
различных машин ![]() , необходимо обработать партию из
, необходимо обработать партию из ![]() однотипных деталей. Обработка детали заключается в последовательном выполнении
однотипных деталей. Обработка детали заключается в последовательном выполнении ![]() операций
операций ![]() . Операция
. Операция ![]() выполняется на машине
выполняется на машине ![]() в течение
в течение ![]() единиц времени,
единиц времени, ![]() . Машины в технологическом маршруте могут повторяться. Прерывания операций запрещены. Одновременное выполнение двух и более операций на одной машине не допускается. Требуется минимизировать общее время обработки всех деталей.
. Машины в технологическом маршруте могут повторяться. Прерывания операций запрещены. Одновременное выполнение двух и более операций на одной машине не допускается. Требуется минимизировать общее время обработки всех деталей.
Эта задача является частным случаем разномаршрутной задачи теории расписаний, которая заключается в минимизации общего времени обработки N деталей на m машинах, но число операций каждой детали и их технологические маршруты различны. Такая задача в англоязычной литературе называется Job-Shop и обозначается ![]() . Она является NP-трудной в сильном смысле. В [4] показано, что задача
. Она является NP-трудной в сильном смысле. В [4] показано, что задача ![]() при условии, что количество обрабатываемых деталей n ограничено константой, разрешима за псевдополиномиальное время. Более того, для ее решения построена вполне полиномиальная аппроксимационная схема трудоемкости
при условии, что количество обрабатываемых деталей n ограничено константой, разрешима за псевдополиномиальное время. Более того, для ее решения построена вполне полиномиальная аппроксимационная схема трудоемкости ![]() , где R – общее число операций всех деталей, а
, где R – общее число операций всех деталей, а ![]() – относительная оценка точности полученного решения [9]. Еще одно важное утверждение доказано в [10]: задача минимизации общего времени с тремя работами
– относительная оценка точности полученного решения [9]. Еще одно важное утверждение доказано в [10]: задача минимизации общего времени с тремя работами ![]() является NP-трудной.
является NP-трудной.
Естественно, утверждения о существовании псевдополиномиального алгоритма и аппроксимационной схемы верны и для частного случая задачи Job-Shop, когда все детали одинаковые. Понятно, что задача с однотипными деталями проще, однако полиномиальных алгоритмов ее решения до настоящего времени не разработано. В данной работе проведен анализ сложности решения этой задачи. В §1 доказывается ее NP-трудность. В §2 рассматривается вопрос использования циклических расписаний при минимизации общего времени обработки однотипных деталей. В §3 введено понятие периодических расписаний, описываются их недостатки и преимущества.
1. Сложность задачи обработки однотипных деталей.
Критерий минимизации общего времени обработки партии деталей является наиболее естественным. Однако, несмотря на простоту формулировки, вопрос о трудности решения задачи обработки однотипных деталей со сложным технологическим маршрутом оставался открытым. В настоящей работе удалось получить ответ на этот вопрос.
Теорема 1. Задача минимизации общего времени обработки однотипных деталей со сложным технологическим маршрутом является NP-трудной.
Доказательство. Рассмотрим NP-трудную разномаршрутную задачу ![]() с тремя машинами
с тремя машинами ![]() и тремя деталями
и тремя деталями ![]() [8]. Сформулируем ее как задачу распознавания. Задано число
[8]. Сформулируем ее как задачу распознавания. Задано число ![]() . Существует ли допустимое расписание выполнения работ длины не более
. Существует ли допустимое расписание выполнения работ длины не более ![]() ? Сведем ее к задаче с тремя идентичными деталями. Без ограничения общности, пусть
? Сведем ее к задаче с тремя идентичными деталями. Без ограничения общности, пусть ![]() и
и ![]() машины, на которых выполняется соответственно первая и последняя операция детали
машины, на которых выполняется соответственно первая и последняя операция детали ![]() . Если эти операции выполняются на одной машине, то обозначим ее
. Если эти операции выполняются на одной машине, то обозначим ее ![]() . Рассмотрим деталь со следующими параметрами:
. Рассмотрим деталь со следующими параметрами:
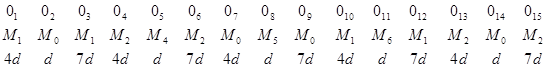
Минимальное время обработки трех таких деталей равна ![]() и достигается на циклическом расписании с длиной цикла
и достигается на циклическом расписании с длиной цикла ![]() . Все прочие расписания имеют длину, по крайней мере,
. Все прочие расписания имеют длину, по крайней мере, ![]() . Расписание изображено на рисунке 1.
. Расписание изображено на рисунке 1.

Рис. 1. Оптимальное расписание для трех деталей.
Номера машин подписаны. Операции каждой детали обрабатываются без простоев, и операция ![]() второй детали выполняется только после завершения операции
второй детали выполняется только после завершения операции ![]() первой детали. Теперь операции
первой детали. Теперь операции ![]() заменим соответственно на последовательность операций деталей
заменим соответственно на последовательность операций деталей ![]() . Заметим, что суммарная длительность операций каждой из деталей
. Заметим, что суммарная длительность операций каждой из деталей ![]() не превосходит
не превосходит![]() . Получим деталь со следующей последовательностью операций:
. Получим деталь со следующей последовательностью операций:
![]()
Рассмотрим задачу составления расписания для трех таких деталей. Покажем, что для нее расписание длины не более ![]() существует тогда и только тогда, когда для разномаршрутной задачи с деталями
существует тогда и только тогда, когда для разномаршрутной задачи с деталями ![]() существует расписание длины не более чем
существует расписание длины не более чем ![]() . Очевидно, что в расписании минимальной длины порядок выполнения операций выглядит следующим образом:
. Очевидно, что в расписании минимальной длины порядок выполнения операций выглядит следующим образом:

Рис. 2. Схема расположения операций деталей ![]() в оптимальном расписании.
в оптимальном расписании.
В одну сторону доказательство очевидно. Если для деталей ![]() и
и ![]() существует расписание длины не более чем
существует расписание длины не более чем ![]() , то для пар
, то для пар ![]() и
и ![]() тем более существует расписание длины не более чем
тем более существует расписание длины не более чем ![]() , и изображенное на рисунке 2 расписание имеет длину не более
, и изображенное на рисунке 2 расписание имеет длину не более ![]() .
.
Теперь в другую сторону. Прежде всего, на рисунке 3 выделим в расписании операции, сдвиг которых может влиять на общую длину расписания.

Рис. 3. Множество возможных критических работ.
Пусть для деталей ![]() не существует расписания длины
не существует расписания длины ![]() . Это означает, что длина оптимального расписания больше
. Это означает, что длина оптимального расписания больше ![]() . Выделим в оптимальном расписании критический путь. Критический путь – это такая последовательность непрерывно выполняемых операций, сдвиг любой из которых приводит к увеличению длины расписания. Уменьшить критический путь тоже нельзя. Осталось заметить, что совместная обработка деталей
. Выделим в оптимальном расписании критический путь. Критический путь – это такая последовательность непрерывно выполняемых операций, сдвиг любой из которых приводит к увеличению длины расписания. Уменьшить критический путь тоже нельзя. Осталось заметить, что совместная обработка деталей ![]() ограничена окном длины
ограничена окном длины ![]() , расположенным в середине расписания на рисунке 3. Действительно, детали
, расположенным в середине расписания на рисунке 3. Действительно, детали ![]() и
и ![]() ограничены с обеих сторон критическими работами, сдвигать которые нельзя. Операции детали
ограничены с обеих сторон критическими работами, сдвигать которые нельзя. Операции детали ![]() также ограничены с обеих сторон, так как первая операция этой детали обрабатывается на машине
также ограничены с обеих сторон, так как первая операция этой детали обрабатывается на машине ![]() , а последняя на
, а последняя на ![]() или
или ![]() . А критический путь оптимального расписания имеет длину больше
. А критический путь оптимального расписания имеет длину больше ![]() . Противоречие. Теорема доказана.
. Противоречие. Теорема доказана.
В доказательстве показано, что для решения задачи с однотипными деталями в случае сложного технологического маршрута фактически приходится решать разномаршрутную задачу Job-Shop. Проведем структурный анализ сложности задачи, в зависимости от входных параметров. Задача Job-Shop является NP-трудной в сильном смысле, но если число деталей фиксировано, то задача NP-трудна в обычном смысле и псевдополиномиально разрешима. Как следствие, задача минимизации общего времени обработки фиксированного числа однотипных деталей будет псевдополиномиально разрешима. Таким образом, доказанный в теореме результат означает, что трудность задачи определяется длительностями операций, а от количества операций n зависимость полиномиальная. Однако остается открытым вопрос о сложности задачи в зависимости от числа деталей N.
2. Подходы к решению задачи.
При обработке однотипных деталей удобно использовать так называемые циклические расписания. Обозначим через ![]() время начала выполнения операции
время начала выполнения операции ![]() детали
детали ![]() . Расписание называется циклическим, если для любого
. Расписание называется циклическим, если для любого ![]() и для любого
и для любого ![]() выполняется
выполняется ![]() , где
, где ![]() – длина цикла или циклическое время. Циклические расписания играют важную роль в организации производства. Они обеспечивают ритмичность загрузки оборудования и исполнителей, позволяют эффективно планировать как поставки ресурсов, так и сбыт продукции. Задача построения расписания с минимальной длиной цикла полиноминально разрешима. Минимальное время цикла
– длина цикла или циклическое время. Циклические расписания играют важную роль в организации производства. Они обеспечивают ритмичность загрузки оборудования и исполнителей, позволяют эффективно планировать как поставки ресурсов, так и сбыт продукции. Задача построения расписания с минимальной длиной цикла полиноминально разрешима. Минимальное время цикла ![]() есть сумма операций на самой загруженной машине.
есть сумма операций на самой загруженной машине.
В данном параграфе исследуется возможность использования оптимальных циклических расписаний при минимизации общего времени обработки всех деталей. Такой подход развивается в работах [5; 6]. Идея алгоритма из [5] следующая. Строим расписание с минимальным временем цикла и выполняем по нему все N работ. При этом достаточно большими оказываются периоды запуска деталей на производственную линию и их завершение. Эти два блока обработки деталей в начале и в конце приводят к тому, что оптимум в задаче минимизации общего времени обработки всех деталей может не достигаться. Но если N растет, то в пределе получаем максимальную производительность линии. Следовательно, такой алгоритм будет асимптотически точным. В [6] предложен аппроксимационный алгоритм, в котором отклонение от оптимума не зависит от числа работ. Ключевым моментом является демонстрация того, как относительно легко получить хорошие аппроксимационные решения для задач с однотипными деталями.
Таким образом, оптимальное значение длины цикла обеспечивает асимптотическую точность алгоритма. Недостатками такого подхода являются длительное время обработки каждой детали, возникающие простои, промежуточное хранение и дополнительная транспортировка, а также издержки, связанные с запуском всей партии в производство. Ниже предлагается алгоритм, который частично нивелирует эти недостатки.
Приведем формальное описание алгоритма.
Шаг 0. Находим C*, равное суммарной длительности операций на самой загруженной машине.
Шаг 1. Все операции первой детали выполняем последовательно без простоев, начиная с нулевого момента времени.
Шаг k. Полагаем t(j, k) = t(j, k-1) + C* и, начиная с последней, устанавливаем все операции этой детали в соответствии с этим расписанием. Если очередную операцию поставить нельзя, то сдвигаем операции предыдущих деталей, пересчитывая расписание.
Алгоритм заканчивает свою работу, когда очередная деталь устанавливается уже без сдвига операций.
Теорема 2. Предложенный алгоритм построения циклических расписаний минимизирует время цикла и является асимптотически точным для задачи минимизации общего времени обработки однотипных деталей.
Доказательство. Минимизация времени цикла непосредственно следует их из построения, так как в цикле машина с максимальной загрузкой не простаивает. Как было сказано выше, минимальная длина цикла С* совпадает с загрузкой этой машины. Пусть обработка одной детали растянулась на K циклов. Заметим, что K не зависит от количества деталей N. Первая деталь завершится не позднее момента KС*. После этого каждая последующая деталь будет выпускаться через промежуток времени, равный С*, и все детали завершаются не позднее KС*+(N-1) С*. С другой стороны, расписание не может иметь длину меньше, чем NС*. Тогда относительная оценка предложенного алгоритма для критерия общего времени завершения работ не превзойдет величины ![]() . Так как K от N не зависит, то при
. Так как K от N не зависит, то при ![]() оценка стремится к нулю, то есть алгоритм является асимптотически точным.
оценка стремится к нулю, то есть алгоритм является асимптотически точным.
Отметим, что предложенный алгоритм, в отличие от подхода из [5], направлен, в том числе, и на уменьшение значения K, и получаемые оценки относительной погрешности будут лучше.
3. Периодические расписания.
Расписание называется L-периодическим со временем периода T, если для каждого j=1,2,...,n и натурального k>L выполняется t(j, k) = t(j, k-L) + T, где t(j, k) – время начала выполнения операции j детали k, а L – количество деталей в периоде. Циклические расписания, рассматриваемые в предыдущем параграфе, являются 1-периодическими. Поэтому периодические расписания являются более широким классом и, естественно, оптимальное значение общего времени завершения работ в этом классе расписаний должно быть не больше, чем в классе циклических. При фиксированном L задача построения L-периодического расписания также полиномиально разрешима. Возникает вопрос, насколько существенно может быть улучшена целевая функция?
В работе было проведено исследование различных характеристик L-периодического расписания. Кроме общей длины периода T и времени завершения работ ![]() рассматривалась величина
рассматривалась величина ![]() – максимальное число одновременно обрабатываемых деталей. Она становится важной, когда на производственной линии недостаточно позиций для хранения незавершенных деталей либо затраты на промежуточное хранение и транспортировку велики. Примером производственной линии с таким ограничением является сборка самолетов, когда количество позиций для сборки ограничено. Другим примером может служить химическая обработка деталей. Деталь крепится на оснастку и последовательно обрабатывается в различных резервуарах. Количество одновременно обрабатываемых деталей ограничено числом таких оснасток, которое также фиксировано.
– максимальное число одновременно обрабатываемых деталей. Она становится важной, когда на производственной линии недостаточно позиций для хранения незавершенных деталей либо затраты на промежуточное хранение и транспортировку велики. Примером производственной линии с таким ограничением является сборка самолетов, когда количество позиций для сборки ограничено. Другим примером может служить химическая обработка деталей. Деталь крепится на оснастку и последовательно обрабатывается в различных резервуарах. Количество одновременно обрабатываемых деталей ограничено числом таких оснасток, которое также фиксировано.
Удалось установить, что при заданном H для любого L-периодического расписания с периодом T=LC существует циклическое расписание с таким же значением H и длиной цикла C. Таким образом, несмотря на расширения множества, на котором оптимизируется целевая функция, по этому параметру улучшения не получаем.
Эксперимент показал, что удается сократить общее время обработки всех деталей в период запуска партии и ее завершения. Но основной цикл для L-периодических и циклических расписаний по производительности линий полностью совпадает. То есть при большом количестве деталей циклические расписания сравнимы с L-периодическими, но существенно лучше в смысле ритмичности производства.
Выпишем основные выводы проведенного исследования.
1. Доказано, что задача обработки однотипных деталей при сложном технологическом маршруте не проще общей разномаршрутной задачи теории расписаний.
2. Для построения приближенных решений минимизации общего времени обработки однотипных деталей эффективно использовать оптимальные циклические расписания.
3. Расширение класса изучаемых расписаний от циклических до L-периодических не приводит к улучшению характеристик по критериям средней частоты выпуска готовых деталей, числа одновременного обрабатываемых деталей и других. Кроме того, циклические расписания предпочтительнее L-периодических по критериям регулярности и ритмичности.
4. Можно добиться улучшения для критерия общего времени завершения работ, однако при большом объеме партии существенных выгод L-периодические расписания по сравнению с циклическими не дают, так как улучшения возможны только в начале и в конце расписания.
Рецензенты:
Забудский Геннадий Григорьевич, д.ф.-м.н., профессор, ведущий научный сотрудник лаборатории дискретной оптимизации, Омский филиал института математики им. С.Л. Соболева СО РАН, г. Омск.
Задорин Александр Иванович, доктор физико-математических наук, зав. лабораторией математического моделирования в механике, Омский филиал института математики им. С.Л. Соболева СО РАН, г. Омск.
Библиографическая ссылка
Межецкая М.А., Сервах В.В. ЗАДАЧИ ОБРАБОТКИ ДЕТАЛЕЙ СО СЛОЖНЫМ ТЕХНОЛОГИЧЕСКИМ МАРШРУТОМ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8407 (дата обращения: 09.03.2026).



