Введение
В данной работе рассматривается проблема стратегического управления муниципальными образованиями в России. Анализ публикаций за последние несколько лет показал, что государство в лице федерального уровня власти будет развивать крупные инфраструктурные проекты в больших городах и мегаполисах [5, 7]. По мнению автора, подобная федеральная стратегия является неверной, так как из сферы государственной политики полностью исключают малые и средние муниципальные образования. В связи с этим появляется необходимость обоснования государственной политики в сфере малых муниципальных образований с применением математического аппарата и использованием широкой статистической базы данных, что и выступает в качестве цели исследования.
Исходные данные
Действительно, согласно Всероссийской переписи населения в 2010 г. в малых и средних городах России (с численностью населения до 100 тыс. человек, включая поселки городского типа) проживало 33 % от всего городского населения, в больших (до 250 тыс. чел.) – 13 %, в крупных (до 1 млн чел.) – 27 % и в крупнейших (свыше 1 млн чел.) – 27 % (рис. 1). Характер данного расселения служит обоснованием для формулировки инфраструктурных стратегий поддержки крупных городов на федеральном уровне.

Источник: рассчитано автором по данным Росстата
Рис. 1. Распределение жителей России по типам городских населенных пунктов
Следует отметить, что существует несколько классификаций городов в зависимости от их размера. По численности населения согласно Градостроительному кодексу они классифицируются на следующие категории [6, с. 99]:
- малые (до 50 тыс. чел.),
- средние (50 – 100 тыс. чел.),
- большие (100 – 250 тыс. чел.),
- крупные (250 – 1000 тыс. чел.),
- крупнейшие (свыше 1 млн. чел.).
Очень важна граница, отделяющая малые и средние города, около 100 тыс. чел. Переходя этот рубеж, города начинают приобретать новые качества.
С другой стороны, можно сделать аналогичный структурный анализ не по населенным пунктам, а в разрезе муниципальных образований (МО). Указанное деление территории страны осуществляется с целью государственного управления согласно федеральному закону № 131-ФЗ «Об общих принципах организации местного самоуправления в РФ». Все МО делятся на городские округа, муниципальные районы и поселения, к которым относятся сельские и городские. Статус городского округа присваивается, как правило, большой по населению территории, например, областному центру. Территории всех поселений, за исключением городских округов, входят в состав муниципальных районов. Границы городского поселения могут отличаться от образующего его одноименного города, например, из-за включения в его состав близлежащих деревень. В Российской Федерации в 2010 г. насчитывалось 1825 муниципальных районов, 516 городских округов (ГО), 1734 городских поселений (ГП), 19126 сельских поселений (СП), а также межсельных территорий – 79; всего 23280 муниципальных образований [2]. В г. Москва число внутригородских территорий города федерального значения составило 125, в г. Санкт-Петербург – 111. В 2010 г. население ГО составило 67 883,4 тыс. чел, ГП – 23844,3 тыс. чел., СП – 34 728,7 тыс. чел. Ниже приводятся данные без Москвы и Санкт-Петербурга (табл. 1).
Таблица 1
Численность и число городских муниципальных образований России
|
|
Всего |
до 100 000 |
100000 – 249999 |
250000 – 499999 |
500000 – 999999 |
1 млн и более |
|
Всего численность населения городских округов и городских поселений, тыс. чел. |
91 728 |
35 344 |
14 302 |
13 972 |
16 219 |
11 891 |
|
Доля населения |
100% |
39% |
16% |
15% |
18% |
13% |
|
Число городских округов и городских поселений |
2250 |
2077 |
96 |
42 |
25 |
10 |
Источник: рассчитано автором по данным Росстата
Таким образом, доля населения, проживающего в крупных городах с населением свыше 100 тыс. чел. составляет 67 % (рис. 1), доля населения в крупных МО (городских округах и поселениях) – 61 % (табл. 1). Если анализировать статистические данные подобным образом, используя критерий численности населения, получается, что в крупных городах, равно как и в крупных муниципальных образованиях проживает большинство жителей нашей страны. На взгляд автора, подобное обоснование является неправомерным, что будет доказано ниже. На актуальность постановки проблемы влияет еще и то, что согласно Конституции Россия является социальным государством, поэтому нельзя вывести 35 млн жителей малых городов за рамки государственной политики.
Рабочая гипотеза
Для целей исследования введем категорию малых и средних МО (МСМО), куда отнесем городские округа и городские поселения численностью не более 100 тыс. человек. Далее сформулируем следующую рабочую гипотезу: в малых и средних муниципальных образованиях проживает большинство населения России, поэтому именно они нуждаются в особой государственной политике и поддержке. Для доказательства применим аппарат теории вероятностей и математической статистики, включая различные законы распределения случайных величин. В отличие от представленной на рис. 1 модели, основанной на структурном анализе, для обоснования гипотезы будет применен критерий не численности, а частоты городских муниципальных образований различного размера и оценена вероятность попадания в интервал, соответствующий размерам МСМО. При этом анализ проводится не в разрезе территориально-административного деления (по населенным пунктам), а в разрезе муниципальных образований. В качестве информационной базы исследования выступают данные Всероссийской переписи населения 2010 г.
Алгоритм расчета и обоснования
Исследование было выполнено в несколько шагов, которые описаны ниже.
1. Были обработаны данные раздела 11 «Численность населения России, федеральных округов, субъектов Российской Федерации, городских округов, муниципальных районов, городских и сельских поселений» Переписи населения [2]. Из всего массива данных были оставлены только строки, содержащие информацию по городским округам и городским поселениям, полученный результат сокращенно приведен в табл. 2. Данные можно рассматривать как выборку из генеральной совокупности для случайной величины – размера городских муниципальных образований, которая является вариационным рядом, то есть, представлена в негруппированном виде и ранжирована.
Таблица 2
Численность населения муниципальных образований России (2010 г.)
|
Наименование муниципального образования |
Размер муниципального образования, чел. |
|
… |
… |
|
Городское поселение Поселок Хани |
764 |
|
Городское поселение рабочий поселок Чистое |
768 |
|
Витимское городское поселение |
773 |
|
Гурское городское поселение |
789 |
|
Городское поселение рабочий поселок Катунки |
806 |
|
Городское поселение поселок городского типа Тенишево |
809 |
|
… |
… |
|
Городской округ город-герой Волгоград |
1 021 215 |
|
Городской округ город Уфа |
1 071 640 |
|
Городской округ Город Ростов-на-Дону |
1 089 261 |
|
Челябинский городской округ |
1 130 132 |
|
Городской округ город Казань |
1 143 535 |
|
Городской округ город Омск |
1 154 116 |
|
Городской округ Самара |
1 164 814 |
|
Городской округ город Нижний Новгород |
1 259 738 |
|
Городской округ муниципальное образование «город Екатеринбург» |
1 383 179 |
|
Городской округ город Новосибирск |
1 473 754 |
Источник: рассчитано автором по данным Росстата.
2. Построим статистический ряд распределения, т.е. перечень вариант и соответствующих им частот. Под вариантой будем понимать размер данного МО в зависимости от численности населения, под частотой варианты – число раз, которое элемент с заданным значением встречается в выборке. Общее число наблюдений равно 2250. Для удобства обработки статистических данных исходную выборку представим в группированном виде с шириной интервала 1 тыс. чел. Для этого подсчитаем частоты – количество элементов выборки, попавших в каждый интервал [4, с. 101]. Также вычислим относительные частоты для каждого интервала как частное от деления частоты на общее количество элементов в выборке. Полученная таблица значений представлена в табл. 3, ввиду большого объема данные указаны не полностью.
Таблица 3
Статистический ряд распределения населения по городским муниципальным образованиям (МО) в зависимости от их размера (численности населения)
|
Границы интервала |
0;1 |
1;2 |
2;3 |
3;4 |
4;5 |
5;6 |
6;7 |
7;8 |
8;9 |
9;10 |
10;11 |
|||||||||
|
Частота (число городских МО) |
46 |
90 |
121 |
141 |
126 |
147 |
118 |
116 |
91 |
76 |
86 |
|||||||||
|
Относительная частота |
0,0204 |
0,040 |
0,0538 |
0,063 |
0,0560 |
0,065 |
0,0524 |
0,052 |
0,040 |
0,034 |
0,038 |
|||||||||
|
Границы интервала |
11;12 |
12;13 |
13;14 |
14;15 |
15;16 |
16;17 |
17;18 |
18;19 |
19; 20 |
20; 21 |
21; 22 |
|||||||||
|
Частота (число городских МО) |
65 |
56 |
49 |
43 |
40 |
34 |
36 |
21 |
17 |
33 |
30 |
|||||||||
|
Относительная частота |
0,029 |
0,025 |
0,022 |
0,019 |
0,02 |
0,015 |
0,016 |
0,009 |
0,008 |
0,015 |
0,013 |
|||||||||
|
… |
||||||||||||||||||||
|
Границы интервала |
90; 91 |
91; 92 |
92; 93 |
93; 94 |
94; 95 |
95; 96 |
96;97 |
97;98 |
98;99 |
99;100 |
||||||||||
|
Частота (число городских МО) |
1 |
1 |
5 |
2 |
4 |
4 |
3 |
1 |
2 |
1 |
||||||||||
|
Относительная частота |
0,0004 |
0,0004 |
0,002 |
0,0009 |
0,0018 |
0,0018 |
0,0013 |
0,0004 |
0,0009 |
0,0004 |
||||||||||
|
… |
||||||||||||||||||||
|
Всего число городских МО |
2250 |
|||||||||||||||||||
Источник: рассчитано автором по данным Росстата.
3. Вычислим некоторые характеристики полученного статистического распределения. Для оценки положения данных на числовой оси используют выборочное среднее, которое служит оценкой математического ожидания генеральной совокупности. По негруппированной выборке оно равно 40,8 тыс. чел. Для описания степени разброса данных относительно центра использовать выборочное среднее квадратическое отклонение, которое для негруппированной выборки равно 115,8 тыс. чел. Характеристикой формы распределения служит выборочный коэффициент асимметрии. В нашем примере он равен 6,85, что свидетельствует о положительной (правосторонней) асимметрии распределения относительно среднего значения. Выборочный коэффициент эксцесса, равный 57, больше 3, что говорит об островершинности полученного распределения по сравнению с нормальным.
4. Для дальнейшего исследования необходимо построить функцию или кривую (плотности) распределения для городских муниципальных образований России в зависимости от их размера. Статистическим аналогом кривой распределения генеральной совокупности является гистограмма частот или относительных частот, которая строится по интервальному вариационному ряду (см. табл. 3). Гистограмма относительных частот представлена ниже на рис. 2.
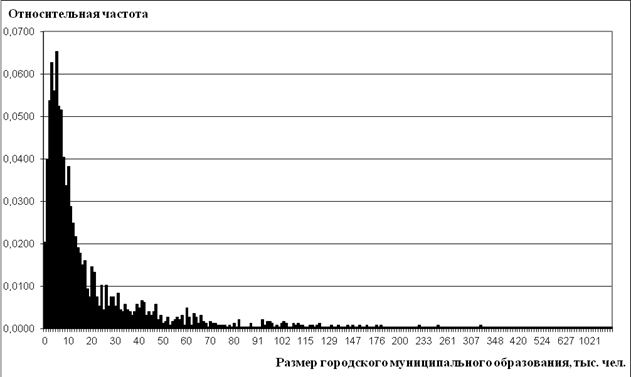
Рис. 2. Гистограмма относительных частот для размера городских муниципальных образований РФ
Гистограмма частот – это ступенчатая фигура, состоящая из прямоугольников с основаниями, равными ширине интервала h и высотами, равными частоте ni или относительной частоте ni/n, где n общее число наблюдений в выборке. Если относительную частоту разделить на ширину интервала, то полученная величина![]() будет являться оценкой функции плотности вероятности в середине соответствующего интервала [4, с. 103]. Для нашего случая при h=1, высота полученной гистограммы равна относительной частоте, отложенной на рис. 2 по оси ординат, которая является вероятностью для середины интервала.
будет являться оценкой функции плотности вероятности в середине соответствующего интервала [4, с. 103]. Для нашего случая при h=1, высота полученной гистограммы равна относительной частоте, отложенной на рис. 2 по оси ординат, которая является вероятностью для середины интервала.
5. В завершении необходимо определить вид полученной кривой. Напомним, что существует несколько законов распределения случайных величин: линейное, нормальное, показательное (экспоненциальное), логнормальное и другие [4, с. 85]. Некоторые авторы полагают, что нормальное распределений встречается чаще по сравнению с другими видами [8]. Оно также имеет свойство – сохранять форму кривой плотности распределения вероятностей, которое было замечено и описано в 1733 году Муавром, а затем исследовано Гауссом. Кривая распределения по нормальному закону имеет симметричный холмообразный вид, максимум которой соответствует точке на оси абсцисс, равной математическому ожиданию.
В нашем исследовании график, изображенный на рис. 2, в целом не соответствует виду нормального распределения. Как было рассчитано в шаге 3, распределение имеет асимметричный холм с правосторонним смещением, характеризуется островершинностью по сравнению с нормальным, а случайная величина X принимает только положительные значения.
6. Далее, для обоснования гипотезы рассчитаем вероятность попадания случайной величины в заданный интервал. Полученный график полностью не соответствует ни одному из видов распределений, по внешнему виду и экономическому содержанию нельзя точно судить о его виде. Для определения закона распределения по статистическим данным, а также нахождения его параметров, проверки критериев правдоподобия гипотез, требуется детальное математическое изучение [1, с. 131-133], которое не может быть выполнено в рамках данной статьи. Поэтому рассчитаем сумму вероятностей попадания в заданный интервал, за который примем диапазон от 0 до 100 тыс. чел. (так как было установлено, что именно такие МО относятся к категории МСМО и требуют особого внимания со стороны государства). Известно, что вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке. [1, с. 78]. На основе данных, представленных в табл. 3, рассчитаем значение эмпирической функции распределения для точек 100 и 0, которая представляет собой накопленные относительные частоты. Вероятность попадания в заданный интервал (0;100) определим как разность между этими значениями (0,9244 и 0,0004 соответственно), которая будет равна 92,4 %. Необходимо добавить, что для проверки полученного результата с помощью функции Microsoft Excel «Персентиль» был рассчитан квантиль для вероятности 92,4 %, который отсек ряд в точке 101. Это показывает, что 92,4 % наблюдений лежат левее указанной точки. Таким образом, проведенные автором расчеты подтверждают ранее выдвинутую гипотезу.
Заключение
Таким образом, в данной статье было показано, что для обоснования и разработки государственной политики в сфере малых и средних муниципальных образований недостаточно проведенного структурного анализа по критерию доли проживающего в них населения. Сложность данного исследования состояла в трудоемкости обработки большого массива данных и приведения их в вид, удобный для анализа. Для научного обоснования автором был применен инструментарий теории вероятностей и математической статистики. Была построена гистограмма вероятностей (относительных частот), которая характеризует закон распределения для размера городских муниципальных образований России. Расчеты показали, что вероятность попадания в заданный интервал, соответствующий численности населения для категории малых и средних муниципалитетов численность населения до 100 тыс. чел., составляет более 90 %. Это подтверждает выдвинутую нами гипотезу о том, что в МСМО проживает большинство населения страны.
Интерпретацией полученных результатов, на взгляд автора, может служить аналогия фотоальбома. Если вклеить на каждую страницу фотографию одного жителя из каждого муниципального образования (города), то вероятность, что, открыв альбом, вы увидите карточку жителя малого и среднего МО, будет составлять около 90 %. Иными словами, это и есть портрет типичного жителя нашей страны, а не крупного центра, как предполагают официальные лица государства.
Тем не менее полученные результаты требуют дальнейшего исследования для практического применения. Так, предлагается разработать стратегии и механизмы прямой государственной поддержки малых и средних муниципальных образований, например, через систему микрогрантов, направленных на поддержку местных инициатив. Такая логическая последовательность согласуется с позицией, на которой стоит автор и которая развивалась в некоторых публикациях [3]: сначала научно обосновать направление государственной политики, и только потом уже определять шаги в рамках данного направления, что должно стать основой концепции стратегического управления.
Рецензенты:
Орлов Андрей Владимирович, д.э.н., профессор, профессор кафедры государственного и муниципального управления ФБГОУ ВПО «Российский экономический университет им. Г. В. Плеханова», г. Москва.
Гретченко Анатолий Иванович, д.э.н., профессор, профессор кафедры национальной и региональной экономики ФБГОУ ВПО «Российский экономический университет им. Г. В. Плеханова», г. Москва.
Библиографическая ссылка
Лукьянова М.Н. ГОСУДАРСТВЕННАЯ СТРАТЕГИЯ РАЗВИТИЯ МАЛЫХ И СРЕДНИХ МУНИЦИПАЛЬНЫХ ОБРАЗОВАНИЙ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8389 (дата обращения: 09.03.2026).



