Несмотря на широкое распространение и использование закрученных потоков газа и значительное количество теоретических и экспериментальных исследований, многие вопросы, связанные с их движением, не имеют достаточно строгого математического описания и обстоятельного экспериментального обоснования [9-11]. В целом можно считать, что задача определения полей скоростей в закрученном турбулентном потоке в цилиндрическом канале в общем виде не решена [3].
Аналитическое описание движения закрученного потока основано, как правило, на одном из трех различных подходов [10]. При первом из них течение представляется в виде наложения плоского стока на потенциальное вращение, методика расчета опирается на использование эмпирических коэффициентов и предусматривает определение только гидравлического сопротивления [9]. Во втором подходе для описания движения закрученного потока используется уравнение Бернулли и экстремальный принцип для одной из характеристик потока при сохранении вдоль радиуса канала момента количества движения [2]. Недостатками такого подхода является грубая схематизация течения и отсутствие учета особенностей движения в приосевой зоне канала. Третий подход основан на применении уравнения Бернулли для движения жидкости в спиральной камере [6]. Метод требует предварительного определения ряда характеристик, зависящих от геометрических параметров канала, и не предусматривает определения всех составляющих скорости. Недостатки указанных методов значительно сужают область их применения для расчета закрученного потока и решения многих прикладных задач [9-11].
Группа методов описания осесимметричного движения газа с вращением базируется на использовании дифференциальных уравнений Навье-Стокса, которые упрощаются в зависимости от постановки задачи и принятой физической модели течения, а также уравнений неразрывности, сохранения энергии и состояния с использованием эмпирических зависимостей для вязкости [11]. В наиболее общем случае уравнения движения турбулентного потока записываются в виде уравнений Рейнольдса с осредненными и пульсационными составляющими скорости [5]. Для замыкания системы уравнений необходимо установить связь между осредненными и пульсационными составляющими скорости турбулентного закрученного потока по одной из полуэмпирических теорий турбулентности [1; 12]. Для описания турбулентных течений в рамках полуэмпирических теорий широко используется понятие турбулентной (эффективной) вязкости.
Аналитическое решение системы уравнений движения возможно лишь с применением большого числа упрощающих допущений [4]. Чаще применяются численные методы решения или расчет осуществляется с применением эмпирических зависимостей [9]. В большинстве случаев для описания полей скоростей в закрученном потоке используются эмпирические и полуэмпирические зависимости [9-11].
Так, зависимость окружной (тангенциальной) составляющей скорости Wt от радиуса r часто выражается зависимостью вида Wtrn = const, в которой показатель степени n может принимать значения от -1 (закон вращения твердого тела) до +1 (закон постоянства циркуляции или квазипотенциальное течение) [9-11]. В общем случае конкретный вид функции Wt = f(r) зависит от способа закручивания потока, хотя считается, что на некотором расстоянии от закручивающего устройства (после участка стабилизации) поле окружной составляющей скорости принимает стационарную («естественную») форму [10; 11]. При этом вблизи оси вращения тангенциальная составляющая равна нулю, закон ее изменения в приосевой зоне становится близким к закону вращения твердого тела («квазитвердое вращение»), в периферийной - к закону постоянства циркуляции («квазипотенциальное вращение»), т.е. поле скоростей становится близким по форме к структуре кругового комбинированного вихря Ранкина [7; 8] (рис. 1а). Расположение границы между зонами либо находится опытным путем, либо определяется путем принятия некоторых дополнительных гипотез [9-11].
Иногда для аппроксимации зависимости Wt = f(r) используются более сложные выражения, объединяющие приосевую и периферийную зоны, например (рис. 1б):
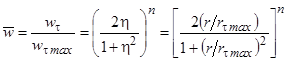 , (1)
, (1)
где`w = Wt/Wtmax - безразмерная тангенциальная скорость; Wtmax - максимальная тангенциальная скорость (на границе зон), м/с; h = r/rtmax - безразмерная радиальная координата, для каналов с осевой цилиндрической вставкой (сердечником) h = (r-rc)/(rtmax-rc); rtmax - наружный радиус приосевой зоны (радиус ядра потока), м; Ra - критический радиус, м; n - постоянная для данной камеры величина (часто принимается n = 1); rc - радиус сердечника.
Существенными недостатками всех существующих расчетных зависимостей для составляющих скорости газа в закрученном потоке газа являются, во-первых, необходимость экспериментального определения или принятия из каких-либо соображений некоторых основных характеристик (в частности, граничного радиуса, максимальной тангенциальной скорости, коэффициентов в эмпирических или полуэмпирических зависимостях и пр.) и, во-вторых, практически все они не учитывают затухание крутки по длине канала, тогда как экспериментальные исследования показывают, что оно может быть существенным даже в коротких трубах.
Единственной возможностью исключения этих недостатков является теоретический анализ движения закрученного потока с максимально полным учетом влияния всех существенных факторов на базе наиболее общих уравнений движения.
а)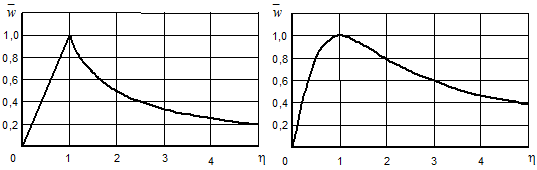 б)
б)
Рис. 1. Аппроксимация профиля тангенциальной составляющей скорости потока:
а - при r < Rв Wt = wr, при r > Rв Wt =C/r, б - по формуле (1) при n = 1
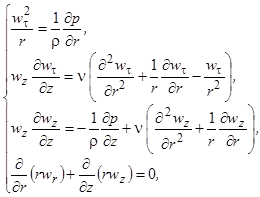 (2)
(2)
где z, r, j - осевая, радиальная и угловая координаты; p - давление, Па; n - кинематическая вязкость газа, м2/c; r - плотность газа, кг/м3.
Второе уравнение системы (2) может быть решено независимо от первого и третьего относительно локальной угловой скорости вращения потока w = ∂(rWt)/(r∂r) = ∂Wt/∂r + Wt/r:
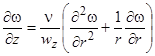 (3)
(3)
или при wz » wср
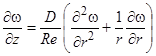 . (4)
. (4)
Уравнение (4) имеет решение в виде:
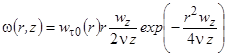 , (5)
, (5)
где Wt0(r) - функция распределения окружной (тангенциальной) скорости во входном сечении канала.
Тогда распределение окружной (тангенциальной) скорости газа по длине и радиусу канала
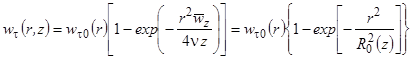 , (6)
, (6)
где R0(z) = (4nтz/`wz)1/2 - характерный (критический) радиус, м [10].
Анализ формулы (6) показывает, что при различных начальных условиях, задаваемых функцией Wt0(r), можно получить различные функции изменения окружных скоростей по длине канала. При потенциальном свободном вихре на входе rWt0(r) = U = const окружная скорость по формуле (6)
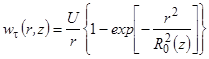 . (7)
. (7)
Тогда в приосевой зоне при r < R0(z) после разложения в ряд
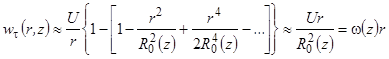 , (8)
, (8)
т.е. в приосевой зоне закон вращения потока близок к закону вращения твердого тела с переменной по длине канала угловой скоростью w(z) = U/R02(z) =`wzU/(4nтz).
В периферийной зоне при r > R0(z) в формуле (7) значение выражения в фигурных скобках приближается к единице и окружная скорость Wt0(r) = U/r, т.е. сохраняет свой профиль аналогичным входному сечению.
Таким образом, при потенциальном свободном вихре на входе поток при движении по каналу из-за вязкости трансформируется в сложный свободно-вынужденный вихрь, аналогичный составному вихрю Ранкина (рис. 2).
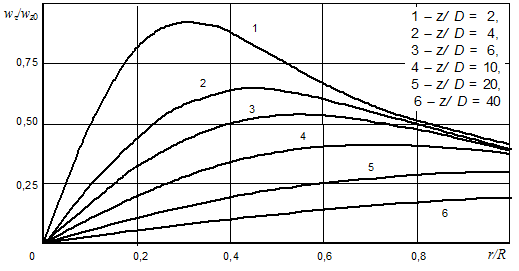
Рис. 2. Распределение окружной скорости при потенциальном вихре на входе:
D = 50 мм, воздух при 20 °С и 1 атм,`wz0 = 20 м/с, U = 0,2 м2/с.
При квазитвердом вращении потока на входе с начальной угловой скоростью w0 (т.е. Wt0(r) = w0r) окружная скорость по формуле (6)
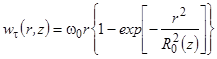 . (9)
. (9)
Тогда в приосевой зоне при r < R0(z) после разложения в ряд получим
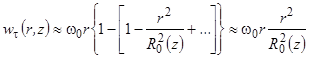 . (10)
. (10)
На оси канала при r = 0 Wt = 0, при r®R0(z) Wt®w0r, т.е. в приосевой зоне, профиль окружной скорости близок к закону вращения твердого тела, хотя и изменяется по длине.
Зависимость (6) подтверждается результатами экспериментальных исследований и является теоретическим обоснованием составного вихря Ранкина [3; 9-11]. Вне зависимости от особенностей закручивающих устройств через определенное расстояние от входа вследствие вязкой диффузии и турбулентной диссипации энергии в закрученном потоке формируется «естественный» профиль скорости. Это предположение является основой инженерных методов расчета закрученных потоков и многих технических устройств [8-11].
Сравнение расчетных профилей скоростей с профилем на рис. 1б показывает, что для инженерных расчетов полученные зависимости могут достаточно точно аппроксимироваться формулой (1).
Относительным недостатком рассмотренной модели закрученного потока и, соответственно, формулы (6) является отсутствие учета вязкого пограничного подслоя на стенке канала, где влияние турбулентности и вихревой вязкости мало. Для более точного определения профиля окружной скорости потока по радиусу канала с учетом анизотропности турбулентности воспользуемся предположением о том, что в ядре потока (вблизи оси канала) при r®0 наблюдается развитое турбулентное течение с большим влиянием вихревой вязкости (nt = n+nв >> n), а вблизи стенки канала при r®R наблюдается вязкое течение (nt = n) и соблюдается условие прилипания (Wt(R,z) = 0). При этом для оценки значения турбулентной вязкости можно использовать известные выражения [10].
Тогда для приосевой зоны на основании формулы (6) коэффициент затухания окружной скорости
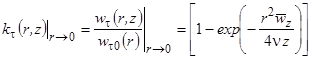 . (11)
. (11)
Для пристенного слоя после внешнего разложения функции (6) методом малых возмущений в точке r = R при Wt(r,z) = 0 и nт = n можно получить
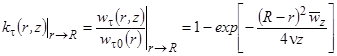 . (12)
. (12)
Составное общее решение для профиля окружной скорости можно получить сращиванием частных асимптотических решений (11) и (12) способом мультипликативного составления [10; 11]:
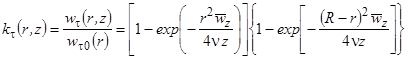 . (13)
. (13)
На рис. 3 показаны зависимости коэффициента затухания окружной скорости kt(r,z) = Wt(r,z)/Wt0(r). Зависимость абсолютного значения окружной скорости в любой точке потока исходя из заданных начальных значений (и, соответственно, изменение профиля окружной скорости по длине канала) можно получить из формулы (13):
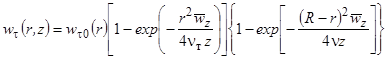 . (14)
. (14)
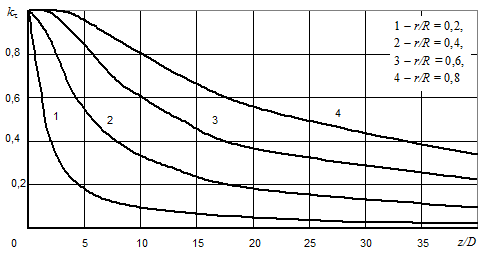
Рис. 3. Изменение коэффициента затухания окружной скорости по длине и радиусу канала: D = 50 мм, wz0 = 20 м/с.
Выражение (14) показывает изменение окружной составляющей скорости вязкого турбулентного закрученного потока несжимаемой жидкости или газа в цилиндрическом канале в функции радиуса и расстояния от входного сечения (рис. 4).
Разработанная методика моделирования турбулентных закрученных потоков может использоваться при анализе, интенсификации и повышении эффективности гидродинамических, тепло- и массообменных процессов, моделировании и расчетах процессов и аппаратов химических технологий, очистки промышленных газовых выбросов [9].
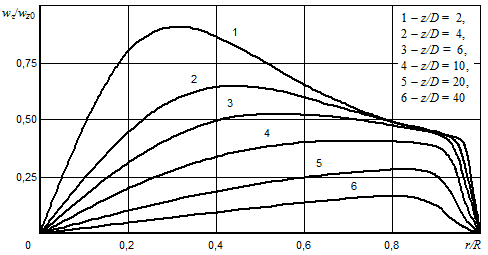
Рис. 4. Распределение окружной скорости по радиусу с учетом пристенного слоя при потенциальном свободном вихре на входе:
D = 50 мм, wz0 = 20 м/с, U = 0,2 м2/с.
Рецензенты:
Хакимзянов Гаяз Салимович, доктор физико-математических наук, профессор, ведущий научный сотрудник, Институт вычислительных технологий СО РАН, г. Новосибирск.
Чекалов Лев Валентинович, доктор технических наук, генеральный директор ЗАО «Кондор-Эко», Ярославская область, п. Семибратово.
Библиографическая ссылка
Сугак Е.В., Сугак А.В. МОДЕЛИРОВАНИЕ ТУРБУЛЕНТНЫХ ЗАКРУЧЕННЫХ ПОТОКОВ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8312 (дата обращения: 13.03.2026).



