Введение
В работах [2; 3] были предложены структуры, с помощью которых можно синтезировать нерекурсивные цифровые фильтры с уменьшенной величиной вычислений. Пример такой структуры приведён на рис. 1. Как видно, приведённая структура состоит из элемента задержки и сумматора.
В [4] были исследованы основные закономерности при разработке нерекурсивных фильтров с использованием вышеприведённых структур, а также было предложено два варианта синтеза структуры таких цифровых фильтров. Следует отметить, что главное достоинство этих фильтров – уменьшенная величина программно-аппаратных затрат при их реализации, т.к. в его структурных компонентах отсутствуют умножители. Учитывая особенности современной аппаратной базы для реализации цифровых фильтров – ПЛИС, данное достоинство приобретает первостепенное значение. Функциональность ПЛИС зависит от количества размещённых на ней устройств обработки. Каждое устройство, размещаемое на ПЛИС, использует определённое количество её ресурсов. Одними из наиболее критичных элементов в ПЛИС являются умножители. В состав каждой ПЛИС входит фиксированное количество умножителей, которые могут быть использованы для построения определённого числа систем, либо одной сложной схемы, поэтому для оптимального использования ресурсов ПЛИС необходимо минимизировать число ненулевых коэффициентов фильтра, что позволит уменьшить количество используемых умножителей, а значит освободить место для других устройств, сократив, таким образом, программно-аппаратные, а значит и материальные затраты.
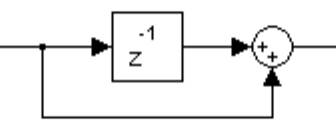
Рис. 1. Элементарное звено фильтра без умножений.
Однако у такого класса фильтров – без умножителей есть целый ряд недостатков, которые сильно ограничивают возможности их использования при построении современных систем цифровой обработки сигналов ЦОС. К таким недостаткам относятся: сложность процедуры синтеза фильтра с произвольной полосой пропускания и подавлением вне полосы, трудности при аппаратной реализации фильтра, связанные с округлением результатов промежуточных арифметических операций. Первый недостаток связан с тем, что данный класс фильтров имеет импульсные характеристики с целыми коэффициентами, соответственно фильтры этого класса при использовании классических структур имеют строго определённые частоты подавления, равные 1/2ω, 1/3ω, 1/4ω, 1/5ω и т.д.

Рис. 2. Схема работы фильтра-дециматора.
Всё это приводит к тому, что фильтры такого класса редко используют самостоятельно. Чаще всего их используют в каскаде с классическими нерекурсивными фильтрами, отводя роль входного фильтра, понижающего частоту, – фильтра-дециматора. Фильтр-дециматор работает по схеме, изображённой на рис. 2. Децимация, как правило, используется в высокоскоростных системах для понижения частоты дискретизации входного сигнала и сокращения аппаратных затрат. В процессе цифровой обработки сигналов нередко возникает задача фильтрации сигнала в очень узком частотном диапазоне. Примером такой задачи может служить ситуация, когда сигнал содержит несколько составляющих на близких частотах и требуется выделить одну из них. Для этого необходимо спроектировать цифровой фильтр с очень узкими относительными полосами пропускания и перехода. В зависимости от расположения составляющих сигнала это может быть фильтр нижних, верхних частот, полосовой или заграждающий фильтр. Прямое проектирование таких устройств часто приводит к фильтрам очень высоких порядков, практическая реализация которых либо нерациональна, либо невозможна. Альтернативный путь решения такой задачи заключается в использовании идей многочастотной дискретизации – последовательном прохождении сигнала через фильтры с изменением частоты дискретизации. Использование многочастотной дискретизации иллюстрирует рис. 3.
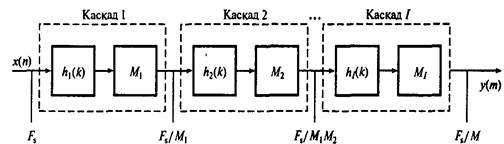
Рис. 3. Процесс многокаскадной децимации.
Каждый каскад представляет собой собственно фильтр (hi) и дециматор (Mi). В каскадной структуре частота преобразуется в несколько этапов. В процессе прохода через каскадный фильтр частота дискретизации понижается постепенно, что приводит к существенному понижению требований к фильтрам защиты от наложения спектров и подавления зеркальных частот каждого каскада.
Общий шаг децимации выражается как произведение меньших шагов [1]:
![]() ,
,
где целое число Мi – шаг децимации N-го каскада. Каждый каскад – это независимый дециматор, обозначенный пунктирным прямоугольником. Если М>1, многокаскадный подход приводит к значительному снижению требований к вычислениям и аппаратным ресурсам, ослаблению характеристик фильтров, используемых в дециматорах а, следовательно, к использованию фильтров, менее чувствительных к эффектам конечной разрядности.
В данном случае в каждом из каскадов используется КИХ-фильтр стандартной структуры, частота дискретизации которого вычисляется по формуле Fs/Mi, где Mi – коэффициент децимации каскада. В результате на выходе последнего каскада частота дискретизации будет равна Fs/M, где M – коэффициент системы. Такая структура системы позволяет существенно уменьшить порядок фильтра, за счёт использования на каждом каскаде фильтров с ослабленными требованиями по отношению к относительной ширине полос пропускания и перехода. Таким образом, суммарные вычислительные, а значит и аппаратные затраты на реализацию системы с многочастотной дискретизацией оказываются значительно меньше по сравнению с прямым проектированием фильтра.
Рассмотрим пример использования каскада из двух фильтров. С одинаковыми характеристиками – полоса пропускания равна половине частоты Найквиста. В качестве «полезного сигнала» будем использовать сумму нескольких синусоид равной амплитуды. В качестве шума – сумму нескольких сигналов с линейной частотной модуляцией (ЛЧМ). Результаты прохождения суммы шума и полезного сигнала через каскад представлены на рисунке 4.
Выбор коэффициента децимации и количества каскадов определяется в зависимости от условий конкретной задачи и параметров системы. Однако следует внимательно подходить к выбору коэффициента децимации. При децимации может наблюдаться эффект наложения – элайзинг (рис. 5), который возникает из-за наложения спектров сигналов друг на друга.
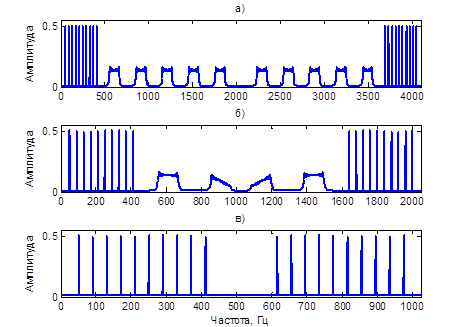
Рис. 4: а) исходный сигнал; б) сигнал после первого фильтра и децимации; в) сигнал после второго фильтра и децимации.
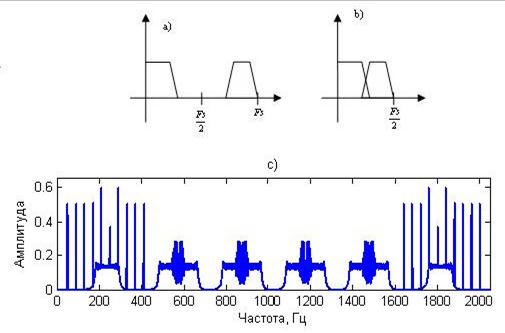
Рис. 5. Иллюстрация эффекта наложения при децимации: а) дискретный спектр исходного сигнала; b) дискретный спектр сигнала после децимации; с) децимация сигнала (рис. 4а) без предварительной фильтрации.
Поэтому максимальный коэффициент децимации будет определяться по формуле [5]:
![]() ,
,
где ![]() – верхняя частота полезного сигнала.
– верхняя частота полезного сигнала.
Если в качестве одного или нескольких каскадов будет выступать фильтр без умножителей, использование которого позволит ещё больше сократить аппаратные затраты по сравнению с использованием КИХ-фильтра стандартной структуры, то качественные показатели фильтрации системы можно будет улучшить за счёт реализации на последнем каскаде КИХ-фильтра с улучшенными параметрами.
Рассмотрим это на примере. В качестве исходного сигнала также использована сумма синусоид («полезная» часть) и ЛЧМ-сигналов (шум). Результаты работы каскадов показаны на рисунке 6.
Таким образом, благодаря высвобождению дополнительных аппаратных и программных ресурсов, появляется возможность реализовать цифровой нерекурсивный фильтр с лучшей прямоугольностью, большим подавлением вне полосы пропускания, меньшим уровнем пульсаций в полосе пропускания. Улучшение каждого из вышеперечисленных параметров приводит к увеличению порядка фильтра, а значит и к росту аппаратных затрат.
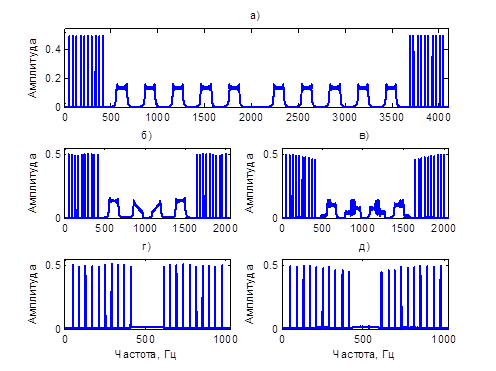
Рис. 6: а) исходный сигнал; б) сигнал после первого КИХ-фильтра и децимации; в) сигнал после фильтра без умножителей; г) сигнал на выходе каскада из двух КИХ-фильтров; д) сигнал на выходе каскада с фильтром без умножителей.
Как видно из рисунка, использование фильтра без умножений в качестве промежуточного в каскаде не привело к существенным изменениям сигнала на выходе каскада.
Рассмотрим распределение аппаратных ресурсов при реализации фильтров-дециматоров в ПЛИС Xilinx Virtex 4 sx35. Пусть целевая полоса составляет 0,125 от исходной частоты Найквиста, частота дискретизации понижается в четыре раза. Синтезируем три схемы: один фильтр (Ф1), каскад из двух фильтров-дециматоров (Ф2) и (Ф3), каскад из фильтра без умножений (Ф4) с децимацией и фильтра-дециматора (Ф3). Параметры фильтров Ф1-Ф3 указаны в таблице 1, Ф4 имеет коэффициенты [1 1 1 1], т.е. состоит из четырёх элементарных звеньев (рис. 1), у каждого из которых имеется одна задержка. Аппаратные затраты сведены в таблицу 2. Разрядность входных данных, выходных данных и коэффициентов фильтра равна 16.
Таблица 1 – Параметры каскада фильтров
|
Фильтр |
Полоса пропускания, доля от fs/2 |
Полоса задерживания, доля от fs/2 |
Неравномерность в ПП, дБ |
Подавление в ПЗ, дБ |
Число коэффициентов |
|
Ф1 |
0,1 |
0,125 |
0,1 |
80 |
266 |
|
Ф2 |
0,2 |
0,3 |
0,1 |
80 |
66 |
|
Ф3 |
0,4 |
0,5 |
0,1 |
80 |
66 |
Таблица 2 – Распределение ресурсов ПЛИС
|
Каскад (фильтр) |
Ресурсы ПЛИС |
|||
|
Блоки (Slice) |
Триггеры |
Таблицы истинности (поиска) 4-LUT |
Блоки ЦОС DSP48 |
|
|
Ф1 |
1177 |
2131 |
1862 |
35 |
|
Ф2+Ф3 |
802 |
1461 |
1097 |
20 |
|
Ф4+Ф1 |
485 |
879 |
590 |
10 |
Результаты синтеза наглядно демонстрируют, что при одинаковом результате (рис. 6) каскад с фильтром без умножителей требует гораздо меньше ресурсов, чем один стандартный КИХ-фильтр или каскад из двух стандартных КИХ-фильтров. Тем не менее, применяя фильтры без умножений при понижении частоты дискретизации, стоит обращать внимание на неравномерность в полосе пропускания на выходе каскада, т.к., как правило, такие фильтры имеют не очень хорошую прямоугольность.
Работа выполнена при поддержке Министерства образования и науки РФ в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009-2013 годы» (Государственный контракт №14.740.11.1148 от 09.06.2011) и «Российского фонда фундаментальных исследований» по конкурсу молодёжных инициативных проектов «Мой первый грант» (соглашение №12-07-31209).
Рецензенты:
Водяхо А.И., доктор технических наук, профессор кафедры ВТ ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Сольницев Р.И., доктор технических наук, профессор кафедры САПР ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Библиографическая ссылка
Каплун Д.И., Канатов И.И., Миненков Д.В. ИСПОЛЬЗОВАНИЕ НЕРЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ БЕЗ УМНОЖЕНИЙ В ЗАДАЧАХ ПОНИЖЕНИЯ ЧАСТОТЫ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8248 (дата обращения: 09.03.2026).



