Проблема обнаружения механизмов рыночного равновесия, действия «пружин» экономической динамики в современной науке значительно обострилась. Глобализация экономики, ускорение экономических и финансовых процессов, их имманентная неустойчивость из-за эндогенной и экзогенной антагонистичности, конкуренции в условиях революционных изменений производственных, технологических, научно-технических, финансовых, внешнеэкономических процессов, явлений и связей, стохастичность поведения объектов на рынке – всё это в полной мере «опускается» на регион и усугубляет проблему пространственной (территориальной) и временной (темпоральной) региональной экономической устойчивости [2]. В основании сложности и противоречивости региональных экономических процессов лежит существенная недетерминированность, присущая самой природе рынка, сетевая структура экономических отношений и тот новый эффект, который Н. Н. Талеб [6] называет «рекурсивностью». Он полагает под ним множество «реактивных пружин, становящихся причиной того, что одни события становятся причиной других событий (например, люди покупают книгу, потому что другие люди её купили, вызывая эффект снежного кома и давая случайный и непредсказуемый результат, который даёт победителю всё). Мы живём в среде, где информация распространяется слишком быстро, увеличивая размах подобных эпидемий. По той же логике события могут случаться потому, что они не должны случиться. (Наша интуиция настроена на среду с более простыми причинно-следственными связями и медленной передачей информации). Подобного рода случайности были редкостью в эпоху плейстоцена, поскольку устройство социально-экономической жизни отличалось примитивностью». Таковы непростые типажи современного регионального рынка.
Следующие от центра неожиданно друг за другом и непредсказуемые на местах событийные возмущения, структурные выбросы, катастрофы, катаклизмы, крахи, скачки, дефолты, обвалы, кризисы, шок, падения в экономике и на фондовом рынке говорят о том, что новые условия хозяйствования, «спустившиеся» в регионы, требуют и новой методологии футурологических исследований. Необходимо «тоньше» представлять экономические процессы, глубже мыслить, обнаруживая всплески не самих показателей, а их производных, статистических моментов, «экономических импульсов», «экономических сил», «экономической кинетической и потенциальной» энергии, полнее учитывать характер современных экономических связей, выделять, обнажать, визуализировать, прогнозировать их, получая, как недавно красиво сказал В. А. Кардаш, «сетевые паттерны причинно-следственных связей» [4].
Последние три десятилетия в теоретической экономике последовательно пересматриваются законы «линейной парадигмы», при этом было найдено, что экономические процессы не следуют нормальному закону распределения. В связи с этим появляется «нелинейная парадигма», отмеченная переходом экономики на синергетическую концепцию, такой переход вызывает необходимость создания принципиально новых математических конструктов и инструментальных средств моделирования. Отнесём к ним фрактальную геометрию, фрактальный анализ, теорию и методы детерминированного хаоса, нейронные сети, линейные клеточные автоматы, нечёткие множества, сплайн-аппроксимацию, фазовые пространства, системы компьютерной математики. Принципиальное преимущество новых подходов состоит в том, что в них первостепенное значение уделяется созданию математических и информационных методов получения качественных (асимптотических) свойств из количественных характеристик исходной модели. Эти качественные показатели не могут быть выведены прямо из свойств элементов системы или из локальных взаимодействий этих элементов.
Природа не является рядом повторяющихся закономерностей, в противоположность этому она характеризуется локальной случайностью и глобальным порядком. Каждый естественный фрактал ограничен в деталях и в то же время подобен любому другому в общей концепции [5]. Другая особенность экономических конъюнктур состоит в сложном и весьма вариативном сочетании их компонент. Структуру экономического сигнала делят на «грубую» и «тонкую» составляющие. В общей структуре мы находим тренд, сезонность, цикличность, стохастический «шум» и событийные составляющие динамики. «Грубые» составляющие – тренд и сезонность – заранее представимы, предсказуемы причины их изменения и форма зависимости, поведение гладкое. Они давно нашли способы своего обнаружения, выделения, представления, объяснения, визуализации и применения. «Тонкая» составляющая – цикличность [7], стохастичность и событийные составляющие – с трудом заранее прогнозируется, причины её появления и проявления не ясны, в этой части структуры стохастика проявляется более чем явно, события происходят спонтанно, планируются с большим трудом.
По этой причине в статье делается упор на предложение новых способов трендового сплайн-прогнозирования региональных маркетинговых процессов, это способы более интеллектуально-сложные, идемпотентные происходящим экономическим перемещениям. Несколько слов о сплайнах, которые в последнее время всё больше и чаще появляются в научных исследованиях по экономике. Сплайном называется «кусочная» функция, представляющая аналитически заданный степенной полином малого порядка (обычно 1–4), которая на разных темпоральных отрезках имеет одну и ту же математическую форму, но разные коэффициенты, так что можно говорить о «кусках» этой функции. Отличительная особенность сплайнов – наличие «узловых точек» на оси абсцисс, образующих «сетку», в этих «узлах» сходятся отрезки, отдельные части сплайна. Есть алгоритм «сшивки», работающий так, чтобы решение и его производные автоматически «сшивались» оптимально в единый ансамбль. Слово «оптимально» означает, что слева и справа от каждой узловой точки будут одинаковыми не только значения функции, но и значения всех её производных, поэтому построенный сплайн-ансамбль будет столь плавным и приятным для глаза. Наиболее частое и простое применение сплайнов – замена табличных, «решётчатых» массивов значений непрерывными аналитическими гладкими кривыми с явно прописанными всеми производными. В англоязычной литературе это применение сплайнов называется “spline-smoothing”, оно на самом деле оказывает «сглаживающий» эффект при представлении дискретных значений экономического показателя. Более «тонкое» применение – раз в переходных экономиках при стохастичном вмешательстве в экономические процессы государства на временных интервалах изменяются условия «экономической игры», варьируются законы, нормы, правила, преференции, налоги, акцизы, пошлины, тарифы, квоты и т.д., то каждый интервал релевантен упомянутым «правилам игры» [3]. В то же самое время модели экономических переменных обязаны автоматически соединяться в непрерывные ансамбли, следуя принципу А. Маршалла – «природа не делает скачков». Сплайны как бы специально созданы для моделирования, анализа, визуализации и прогнозирования «рваной» динамики тех экзогенных условий, в рамках которых протекают «на месте» непрерывные экономические процессы. В фазовом пространстве сплайновые образы вычленяют циклы [7] из временных рядов объёмов продаж (рис. 1).
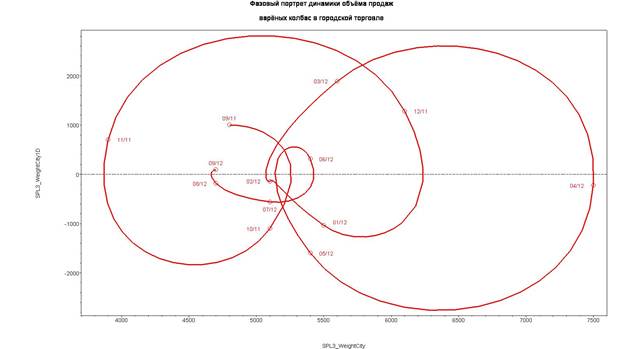
Рисунок 1. Типичный фазовый портрет устоявшейся городской торговли варёными колбасами (RED). Систематическая цикломатика [7] идеальных форм с примерными четырёхмесячными периодами. Кубические сплайны. По оси абсцисс – объём продаж варёных колбас в городской торговле (SPL3_WeightCity), по оси ординат – его первая производная (SPL3_WeightCity1D). Время – сентябрь 2011 (09/11) – сентябрь 2012 (09/12) гг. Увеличивается объём продаж перед праздничными днями – в декабре 2011 и в апреле 2012 гг. Наибольшая скорость продаж – в середине декабря 2011 г., наименьшая – в середине мая 2012 г.
В сплайн-прогнозировании насчитывается, по крайней мере, пять алгоритмов разной степени сложности [1]. Здесь мы предложим, опишем и исследуем основной алгоритм сплайн-прогностических построений, связывающий экзогенные и эндогенные факторы экономического процесса с его окружением («прогностическим фоном»). Сплайн-технологии использованы в горизонте прогноза при изучении динамики деятельности предпринимателя регионального масштаба, поскольку сплайн-моделирование и анализ продемонстрировали свои значительные преимущества перед классическими эконометрическими методами [3].
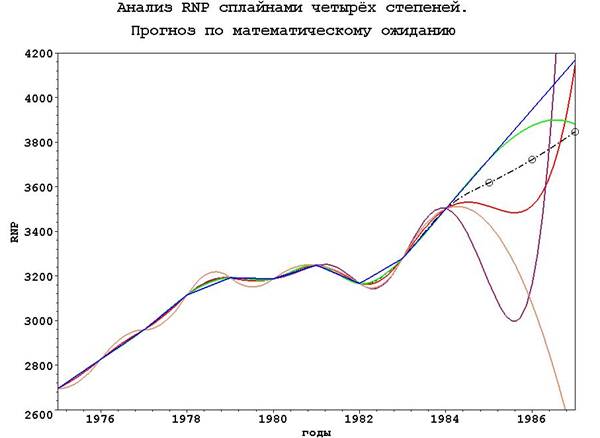
Рисунок 2. Иллюстрация идеи анализа и прогнозирования сплайнами первых четырёх порядков (первого порядка – BLUE, второго – TAN, третьего – GREEN, четвёртого – MAROON, математического ожидания – RED) на примере реального валового национального продукта (RNP) США в 1975–1984 гг. с экстраполяцией в 1985–1988 годы их математического ожидания. Реальное поведение экономики – штрих-пунктир (BLACK). Ошибка прогноза от 3 до 8 %
В исследовании поиск прогноза разделён на два этапа. В качестве исходного приближения используется необычный, не очень точный способ прогнозирования – простая сплайн-экстраполяция. В этой «простой» экстраполяции экспансия сплайна в горизонт прогноза происходит при неизменности двух его характерных величин – «наклона» и «момента» – на последнем интервале отчётного периода [XN-1, XN] и в горизонте прогноза [XN, XZ]. Недостаток подхода – отсутствие связи параметров экстраполяционного продолжения с «математической историей», статистикой поведения процесса в долгом отчётном периоде. Простая экстраполяция содержится в самом аппарате построения сплайнов и успешно напрямую реализуется в системе компьютерной математики MAPLE 16.01. Постараемся косвенно устранить выявленный недостаток на втором этапе при помощи «оптимального статистического обобщения». Полученные сплайнами разных порядков (степеней) частные прогнозы (рис. 2) уточняются и статистически оптимально сводятся к одному показателю, более надёжному.
Известно, что если ищется обобщённое значение нескольких случайных величин (коллективного точного прогноза, например, по частным неточным прогнозам на первом этапе), полученных взаимоисключающими методами, то обобщение или уточнение второго этапе состоит в применении методики «оптимального статистического обобщения». Суть формальных процедур, специфических для исследования, состоит в получении прогнозной системой четырёх частных вариантов прогноза. Каждый q-тый частный вариант прогноза доставляется экстраполяцией сплайна q-той степени qYN (q = 1..Q) в перспективную область [XN, XZ] – от последней точки отчётного периода XN вплоть до точки XZ прогноза, в ней получим Q (в нашем примере Q = 4) значений qYZ.
Будем полагать YZ = G(1YZ, 2YZ, 3YZ, 4YZ; C1, C2, C3, C4), где YZ - обобщённый прогноз в точке аргумента XZ; G – оператор обобщения; qYZ – частные прогнозы, полученные сплайнами q-ых степеней (q = 1..4) простой экстраполяцией, Сq – искомые параметры обобщённого прогноза, соответствующие выбранному критерию.
Начнём искать обобщённое значение прогноза YZ в классе линейных функций:
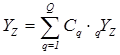 , а в качестве критерия обобщения выберем минимизацию дисперсии ошибки уточнённого прогноза. Для коллективного прогноза YZ воспользуемся известным статистическим правилом, по которому:
, а в качестве критерия обобщения выберем минимизацию дисперсии ошибки уточнённого прогноза. Для коллективного прогноза YZ воспользуемся известным статистическим правилом, по которому:
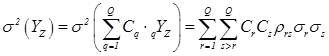 ,
,
где rrs – коэффициент корреляции между текущими (i = 1..N, j = 1..N) отсчётами при получении частных прогнозов сплайнами r-той и s-той степеней rYN и sYN (r = 1..Q, s = 1..Q); sr и ss – соответствующие r-тые и s-тые среднеквадратичные отклонения.
Задача заключается в поиске таких коэффициентов Сr, Cs (r = 1..Q, s = 1..Q), которые минимизировали бы s2(YZ). В работе применён приём, аналогичный методу группового учёта аргументов (МГУА). Вначале строится комбинированная модель для первых двух моделей 1YN и 2YN по следующей усечённой формуле: G12 = C1×1YN + C2×2YN, где С1 и С2 – искомые коэффициенты, минимизирующие дисперсию ошибки синтезируемого прогноза. Условие ![]() приводит к С2 = 1-С1 и тогда 12YN = G12 = C1×1YN + (1–C1)×2YN . Из минимума:
приводит к С2 = 1-С1 и тогда 12YN = G12 = C1×1YN + (1–C1)×2YN . Из минимума:
s2(12YZ) = s2(G12) = 0 находим C1 и С2.
Далее в общем случае строятся попарно функции Grs (r ¹ 1 & s ¹ 2), они попарно же объединяются в комплекс G12rs для получения модели rsYN. В нашем частном случае берутся частные прогнозы: 3YN и 4YN, для них С4 = 1-С3 и 34YN= G34 = C3×3YN + (1-C3)×4YN. Комплекс
Yj = G1234 = C5×(C1×1YN + (1-C1)×2YN) + C6×(C3×3YN + (1-C3)×4YN)
работает в интервале до XN, коэффициент C6 = 1-C5. Когда модель доходит до XZ,
YZ = D1×1YZ + D2×2YZ + D3×3YZ + D4×4YZ ,
где D1 = C1×C5; D2 = (1-C1)×C5; D3 = C3×(1-C5); D4 = (1-C3)×(1-C5).
Способ использует принципиальную разницу поведения сплайнов нечётных и чётных степеней при анализе и прогнозировании. По частным прогнозным кривым qYZ, одновременно генерируемым сплайнами q-тых степеней (q = 1..4), строится кривая математического ожидания с найденными коэффициентами Dq при каждом слагаемом, она и становится образом обобщённого прогноза. Обоснованность конечного прогноза YZ будет выше изолированных локальных прогнозов 1YZ, 2YZ, 3YZ, 4YZ,, так как в нём оптимально (с минимумом дисперсии ошибки) синтезируются результаты, получаемые по четырём частным прогнозам.
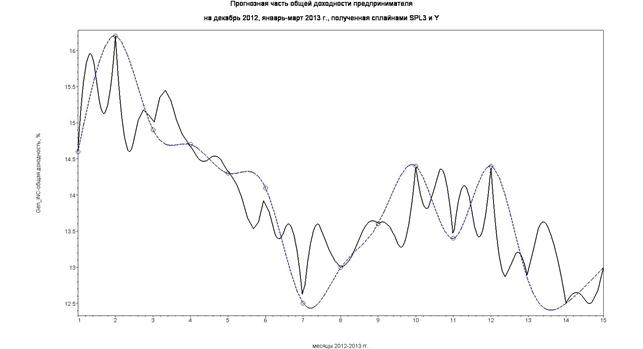
Рисунок 3. Сплайн-образы оптимально статистически обобщённой кривой ZYN (сплошная точная линия – BLACK) и кубической кривой SPL3 (пунктирная приближённая линия – NAVY) динамики общей доходности предпринимателя в январе-ноябре 2012 г. и обобщённого прогноза на декабрь 2012 (месяц № 12), январь – март 2013 г. (месяцы № 13–15)
Предлагаемый алгоритм прогнозирования:
10 вычисляются простой сплайн-экстраполяцией четыре частных сплайн-прогноза экономического показателя;
20 методом «оптимального (по критерию минимума дисперсии) статистического обобщения» вычисляются коэффициенты Сq при слагаемых коллективного прогноза;
30 строится кривая математического ожидания (кривая обобщённого прогноза) с рассчитанными на последнем шаге коэффициентами Dq.
Проведены эксплуатационные операции «погружения» алгоритма в задачи сплайн-прогнозирования динамики обеспечения населения региона продовольственными продуктами. На рис. 3 приведены результаты прогнозирования на декабрь 2012 и январь – март 2013 г. динамики суммарной доходности предпринимателя, реализующего обеспечение колбасными изделиями фирмы «Микоян» города Черкесска в Карачаево-Черкесской Республике.
Рецензенты:
Винтизенко Игорь Георгиевич, доктор технических наук, профессор, ведущий научный сотрудник Научно-педагогического института Северо-Кавказского федерального университета, г. Ставрополь.
Тимошенко Николай Константинович, доктор экономических наук, профессор, профессор кафедры «Экономика, бухгалтерский учёт и аудит» Невинномысского технологического института (филиал) ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Невинномысск.
Библиографическая ссылка
Узденова Ф.М. СПЛАЙН-ПРОГНОЗИРОВАНИЕ ПОВЕДЕНИЯ РЕГИОНАЛЬНОГО ПРЕДПРИНИМАТЕЛЯ В РЕАЛИЯХ РОССИЙСКОЙ ЭКОНОМИКИ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8216 (дата обращения: 09.03.2026).



