Развитие асинхронного электропривода с векторным управлением
Принято различать два основных способа управления электроприводами переменного тока, использующими в качестве преобразователей энергии полупроводниковые преобразователи частоты: частотное и векторное.
При частотном управлении в ЭП реализуется один из статических законов частотного управления (например, ![]() ,
, ![]() ,
,![]() и т.д.). На выходе системы управления формируется задание по частоте и амплитуде выходного напряжения ПЧ. Область применения таких систем: асинхронный электропривод, к которому не предъявляется повышенных статических и динамических требований, вентиляторы, насосы и прочие общепромышленные механизмы.
и т.д.). На выходе системы управления формируется задание по частоте и амплитуде выходного напряжения ПЧ. Область применения таких систем: асинхронный электропривод, к которому не предъявляется повышенных статических и динамических требований, вентиляторы, насосы и прочие общепромышленные механизмы.
При векторном управлении управление осуществляется по мгновенным значениям переменных. В цифровых векторных системах может выполняться управление по эквивалентным (усредненным на интервале дискретности управления) переменным [1].
В 1971 году Блашке предложил принцип построения системы управления асинхронным двигателем [5], в котором использовалась векторная модель АД с ориентацией системы координат по потокосцеплению ротора. Этот принцип называется также прямым управлением моментом [3]. Векторное управление позволяет существенно увеличить диапазон управления, точность регулирования, повысить быстродействие электропривода. Этот метод обеспечивает непосредственное управление вращающим моментом двигателя.
Вращающий момент определяется током статора, который создает возбуждающее магнитное поле. При непосредственном управлении моментом необходимо изменять, кроме амплитуды, и фазу статорного тока, то есть вектор тока. Этим и обусловлен термин «векторное управление».
Для управления вектором тока, а, следовательно, положением магнитного потока статора относительно вращающегося ротора требуется знать точное положение ротора в любой момент времени. Задача решается либо с помощью выносного датчика положения ротора, либо определением положения ротора путем вычислений по другим параметрам двигателя. В качестве этих параметров используются токи и напряжения статорных обмоток.
Менее дорогим является частотно регулируемый электропривод с векторным управлением без датчика обратной связи скорости, однако векторное управление при этом требует большого объема и высокой скорости вычислений от преобразователя частоты. Кроме того, для непосредственного управления моментом при малых, близких к нулевым скоростям вращения работа частотно-регулируемого электропривода без обратной связи по скорости невозможна. Векторное управление с датчиком обратной связи по скорости обеспечивает диапазон регулирования до 1:1000 и выше, точность регулирования по скорости – сотые доли процента, точность по моменту – единицы процентов [6].
Питание АД и СД в режиме векторного управления осуществляется от инвертора, который может обеспечить в любой момент времени требуемые амплитуду и угловое положение вектора напряжения (или тока) статора. Измерение амплитуды и положение вектора потокосцепления ротора производится с помощью наблюдателя (математический аппарат, позволяющий восстанавливать неизмеряемые параметры системы). В зависимости от условий эксплуатации электропривода возможно управление электродвигателем как в режимах с обычной точностью, так и в режимах с повышенной точностью отработки задания на скорость или момент. Так, например, частотный преобразователь обеспечивает точность поддержания скорости вращения ±2-3% в режиме U/f, при векторном управлении без датчика скорости ±0,2%, при полном векторном управлении с датчиком скорости обеспечивается точность ±0,01% [4].
Общий принцип векторного управления АД
В дальнейшем мы будем использовать следующие индексы систем координат: a-b – неподвижная система координат (![]() ), ориентированная по оси фазы a обмотки статора; x-y – система координат, вращающаяся синхронно с ротором (
), ориентированная по оси фазы a обмотки статора; x-y – система координат, вращающаяся синхронно с ротором (![]() ) и ориентированная по оси фазы a его обмотки; d-q – система координат, вращающаяся синхронно с потокосцеплением ротора (
) и ориентированная по оси фазы a его обмотки; d-q – система координат, вращающаяся синхронно с потокосцеплением ротора (![]() ) и ориентированная по его направлению; m-n – произвольно ориентированная система координат, вращающаяся с произвольной скоростью
) и ориентированная по его направлению; m-n – произвольно ориентированная система координат, вращающаяся с произвольной скоростью ![]() .
.
Общий принцип моделирования и построения системы управления АД заключается в том, что для этого используется система координат, постоянно ориентированная по направлению какого-либо вектора, определяющего электромагнитный момент. Тогда проекция этого вектора на другую ось координат и соответствующее ей слагаемое в выражении для электромагнитного момента будут равны нулю, и формально оно принимает вид, идентичный выражению для электромагнитного момента двигателя постоянного тока, который пропорционален по величине току якоря и основному магнитному потоку.
В случае ориентации системы координат по потокосцеплению ротора (![]() ) момент можно представить как:
) момент можно представить как:
![]() , (1)
, (1)
где ![]() – индуктивность рассеяния цепи ротора,
– индуктивность рассеяния цепи ротора, ![]() – индуктивность цепи намагничивания,
– индуктивность цепи намагничивания, ![]() – число пар полюсов,
– число пар полюсов, ![]() – проекции токов статора на оси системы координат
– проекции токов статора на оси системы координат ![]() .
.
По данному выражению можно при условии постоянства потокосцепления ротора управлять электромагнитным моментом, изменяя проекции тока статора на поперечную ось ![]() . Выбор уравнения для построения системы управления играет большую роль, т.к. многие величины, в особенности у короткозамкнутых АД, не могут быть измерены. Кроме того, этот выбор существенно влияет на сложность передаточных функций системы, иногда в несколько раз увеличивая порядок уравнений.
. Выбор уравнения для построения системы управления играет большую роль, т.к. многие величины, в особенности у короткозамкнутых АД, не могут быть измерены. Кроме того, этот выбор существенно влияет на сложность передаточных функций системы, иногда в несколько раз увеличивая порядок уравнений.
Для построения системы векторного управления АД нужно выбрать вектор, относительно которого будет ориентирована система координат, и соответствующее выражение для электромагнитного момента, а затем определить входящие в него величины из уравнений для цепи статора и/или ротора (2) [3]:
![]() , (2, а)
, (2, а)
![]() , (2, б)
, (2, б)
где ![]() – напряжение обмоток статора в векторной форме;
– напряжение обмоток статора в векторной форме; ![]() – активные сопротивления обмоток статора и ротора; составляющие
– активные сопротивления обмоток статора и ротора; составляющие ![]() ,
,![]() связаны с изменением потокосцепления во времени вследствие изменения во времени токов и называются ЭДС трансформации, по аналогии с процессами ее возбуждения в соответствующей электрической машине; составляющие
связаны с изменением потокосцепления во времени вследствие изменения во времени токов и называются ЭДС трансформации, по аналогии с процессами ее возбуждения в соответствующей электрической машине; составляющие ![]() ,
, ![]() – связаны с изменением потокосцепления вследствие вращения ротора и называются ЭДС вращения.
– связаны с изменением потокосцепления вследствие вращения ротора и называются ЭДС вращения.
Если в качестве опорного вектора выбрать потокосцепление ротора и ориентировать по нему координатную систему так, чтобы ее вещественная ось совпадала с направлением ![]() , то угловая частота вращения системы координат
, то угловая частота вращения системы координат ![]() будет равна угловой частоте питания статора
будет равна угловой частоте питания статора ![]() , т.к. векторы потокосцеплений статора и ротора вращаются с одинаковой частотой. Применение вектора потокосцепления ротора теоретически обеспечивает большую перегрузочную способность АД.
, т.к. векторы потокосцеплений статора и ротора вращаются с одинаковой частотой. Применение вектора потокосцепления ротора теоретически обеспечивает большую перегрузочную способность АД.
При этом проекции вектора тока статора с учетом того, что ![]() , равны:
, равны:
![]() (3)
(3)
где ![]() – электромагнитная постоянная времени ротора.
– электромагнитная постоянная времени ротора.
Выразим потокосцепление и угловую частоту ротора:
![]() (4)
(4)
Таким образом, с помощью проекции тока статора ![]() можно управлять потокосцеплением ротора, и передаточная функция этого канала соответствует апериодическому звену с постоянной времени, равной постоянной времени ротора; а с помощью проекции
можно управлять потокосцеплением ротора, и передаточная функция этого канала соответствует апериодическому звену с постоянной времени, равной постоянной времени ротора; а с помощью проекции ![]() можно независимо и безынерционно управлять частотой ротора
можно независимо и безынерционно управлять частотой ротора ![]() .
.
При этом электромагнитный момент АД можно определить, зная частоту токов ротора при заданном потокосцеплении:
![]() , (5)
, (5)
Выражения (3)–(5) определяют связь между проекциями тока статора на оси координат, потокосцеплением, частотой ротора и электромагнитным моментом АД. Из выражения (5) и уравнения движения следует, что управление моментом может осуществляться безынерционно двумя входными сигналами: потокосцеплением и частотой ротора. Эти сигналы связаны с проекциями вектора тока статора выражениями (4). Поэтому устройство векторного управления содержит блок развязки координат (РК), осуществляющий преобразования в соответствии с выражениями (3), а также ротатор, вращающий вектор тока статора в направлении, противоположном вращению ротора АД. Входными сигналами для устройства управления будут линейное напряжение сети и частота питающего напряжения, соответствующие потокосцеплению и частоте ротора. Название блока развязки координат происходит от выполняемой им функции формирования сигналов, соответствующих независимым (развязанным, разделённым) проекциям вектора тока статора (рисунок 1).
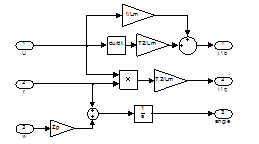
Рис. 1. Структурная схема блока развязки координат.
Из выражения для электромагнитного момента (5) и общего уравнения движения можно получить передаточную функцию АД по каналу управления частотой ротора:
![]() , (6)
, (6)
где ![]() – механическая постоянная времени. Эта передаточная функция полностью соответствует двигателю постоянного тока, поэтому построение систем электропривода с векторным управлением АД ничем не отличается от приводов постоянного тока.
– механическая постоянная времени. Эта передаточная функция полностью соответствует двигателю постоянного тока, поэтому построение систем электропривода с векторным управлением АД ничем не отличается от приводов постоянного тока.
Следует отметить, что устройство управления может выполнять свои функции только при условии, что параметры АД, входящие в передаточные функции его звеньев, соответствуют истинным значениям, в противном случае потокосцепление и частота ротора в АД и в устройстве управления будут отличаться друг от друга. Это обстоятельство создает значительные трудности при реализации систем векторного управления на практике, т.к. параметры АД изменяются в процессе работы. В особенности это относится к значениям активных сопротивлений [3].
Математическое описание координатных преобразований
Если вектор тока представлен в неподвижной системе координат (a, b), то переход к новой системе координат (x,y), развернутой относительно исходной на некоторый угол ![]() (рисунок 2а), осуществляется из следующего соотношения аргументов комплексных чисел:
(рисунок 2а), осуществляется из следующего соотношения аргументов комплексных чисел:
![]() или
или ![]() (7)
(7)
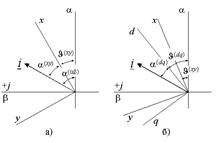
Рис. 2. Обобщенный вектор тока в различных системах координат.
Для системы координат, вращающейся с постоянной угловой частотой ![]() , угол
, угол ![]() равен
равен ![]() .
.
Преобразование координат можно записать в развернутом виде следующим образом:
![]() (8)
(8)
Отсюда можно найти составляющие вектора ![]() и
и ![]() в матричной форме:
в матричной форме:
![]() , (9)
, (9)
где ![]() ,
, ![]() – мгновенные значения токов соответствующих обмоток.
– мгновенные значения токов соответствующих обмоток.
Необходимым элементом системы векторного управления АД является ротатор, осуществляющий преобразование координат векторов в соответствии с выражением (9) [3].
Для преобразования переменных из системы координат (d,q) в систему координат (a, b) воспользуемся следующими уравнениями:
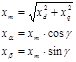 , (10)
, (10)
где γ – угол полеориентирования. Структурная схема ротатора изображена на рисунке 3.
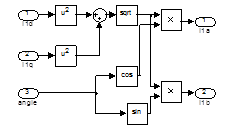
Рис. 3. Структурная схема ротатора.
Математическая модель АД
Асинхронный двигатель смоделирован в системе координат – α, β. Уравнения, соответствующие этой системе координат, описываются системой уравнений:
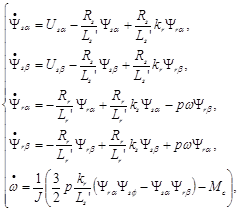 (11)
(11)
где: ![]() ,
, ![]() ,
, ![]() ,
, ![]() – составляющие векторов потокосцепления статора и ротора в системах координат
– составляющие векторов потокосцепления статора и ротора в системах координат ![]() ;
; ![]() ,
, ![]() – составляющие вектора напряжения статора в системах координат
– составляющие вектора напряжения статора в системах координат ![]() ;
;![]() – активные сопротивления обмоток статора и ротора;
– активные сопротивления обмоток статора и ротора; ![]() – полные индуктивности обмоток статора и ротора (17),(18);
– полные индуктивности обмоток статора и ротора (17),(18);![]() – коэффициенты электромагнитной связи статора и ротора (12),(13); p – число пар полюсов;
– коэффициенты электромагнитной связи статора и ротора (12),(13); p – число пар полюсов; ![]() – механическая скорость ротора; J – момент инерции ротора двигателя;
– механическая скорость ротора; J – момент инерции ротора двигателя; ![]() – момент сопротивления на валу двигателя.
– момент сопротивления на валу двигателя.
Значения полных индуктивностей обмоток и коэффициентов электромагнитной связи статора и ротора вычисляются по формулам:
![]() (12)
(12)
![]() (13)
(13)
где:![]() – индуктивности рассеяния;
– индуктивности рассеяния; ![]() – индуктивность цепи намагничивания,
– индуктивность цепи намагничивания,
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
где: ![]() – индуктивное сопротивление рассеяния обмоток статора и ротора;
– индуктивное сопротивление рассеяния обмоток статора и ротора;![]() – индуктивное сопротивление цепи намагничивания; f – частота напряжения, подводимого к статору.
– индуктивное сопротивление цепи намагничивания; f – частота напряжения, подводимого к статору.
![]() (17)
(17)
![]() (18)
(18)
При решении системы дифференциальных уравнений в координатах ![]() (11) можно получить динамическую механическую характеристику и временные характеристики переменных состояния (например, момента и скорости), которые дают представление о процессах, протекающих в двигателе. Составляющие напряжения, подводимого к статорной обмотке двигателя, вычисляются по формуле:
(11) можно получить динамическую механическую характеристику и временные характеристики переменных состояния (например, момента и скорости), которые дают представление о процессах, протекающих в двигателе. Составляющие напряжения, подводимого к статорной обмотке двигателя, вычисляются по формуле:
![]() (19)
(19)
где U – действующее значение напряжения, подводимого к статору.
Решение уравнений сводится к интегрированию левой и правой частей каждого дифференциального уравнения системы:
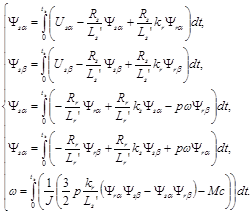 (20)
(20)
Токовременные зависимости вычисляются по уравнениям:
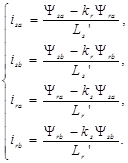 (21)
(21)
Паспортные данные АД ДМТ f 011-6у1 приведены в статье [2].
На рисунке 4 изображена модель АД, управляемого током статора, в системе координат, ориентированной по потокосцеплению ротора.
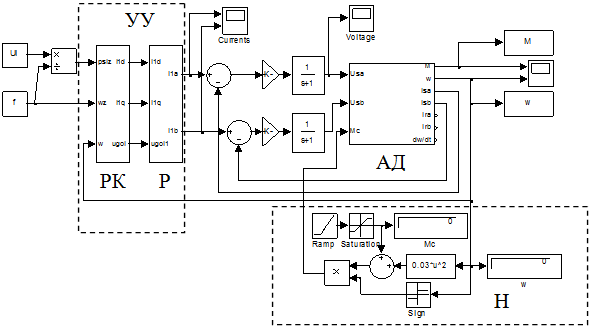
Рис. 4. Модель векторного управления АД в среде Simulink:
АД – асинхронный двигатель;
УУ – устройство управления, включающее: РК – блок развязки координат, Р – ротатор;
Н – нагрузка, учитывающая также сопротивление подшипников.
Модель векторного управления АД позволяет отслеживать электромагнитные процессы, происходящие в асинхронном двигателе при его работе.
На следующем графике (рисунок 5) изображена механическая характеристика электродвигателя при векторном управлении, полученная модельным путем, в сравнении с механической характеристикой электродвигателя без регулятора, полученной при натурном эксперименте [2].
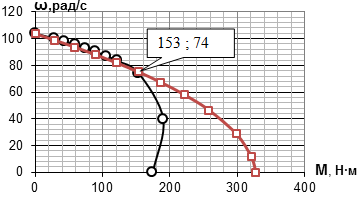
Рис. 5. Сравнение механических характеристик.
Как можно видеть по графику, при векторном управлении механическая характеристика асинхронного двигателя приобретает жёсткость, вследствие чего расширяется перегрузочный диапазон. Значения характеристик в диапазоне от 0 до 153 Н·м расходятся незначительно, погрешность составляет лишь 1,11%, следовательно, полученная математическая модель адекватно отражает работу реального двигателя и её можно использовать для проведения экспериментов в инженерной практике.
Заключение
Применение векторного управления позволяет посредством изменения амплитуды и фазы питающего напряжения напрямую управлять электромагнитным моментом электродвигателя. Для векторного управления асинхронным двигателем следует сначала привести его к упрощенной двухполюсной машине, которая имеет две обмотки на статоре и роторе, в соответствии с этим имеются системы координат, связанные со статором, ротором и полем. Векторное управление подразумевает наличие в звене управления математической модели регулируемого электродвигателя.
Механические характеристики, полученные при работе описанной модели, подтверждают теоретические сведения о векторном управлении. Модель адекватна и может применяться для дальнейших экспериментов.
Рецензенты:
Швецов Владимир Алексеевич, д.т.н., профессор кафедры РЭС КамчатГТУ, г. Петропавловск-Камчатский.
Потапов Вадим Вадимович, д.т.н., профессор филиала ДВФУ, г. Петропавловск-Камчатский.
Библиографическая ссылка
Лиходедов А.Д., Портнягин Н.Н. МОДЕЛИРОВАНИЕ ВЕКТОРНОГО УПРАВЛЕНИЯ АСИНХРОННЫМ ЭЛЕКТРОПРИВОДОМ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8213 (дата обращения: 22.02.2026).



