Введение
Анализ и синтез моделей управления экономическими системами, в частности, мезоуровня, учитывающих различные аспекты инновационного производства, становятся в последнее время особенно актуальными в свете того, что эффективное развитие экономических систем неизбежно требует исследования законов функционирования инновационных процессов в них. Экономические системы, являясь открытыми, обладают не только энергией восприятия инноваций, но и способны вырабатывать синергию как результат взаимодействия нескольких положительных для системы эффектов. При анализе регионального экономического развития принципиальным является использование многокритериальных постановок задач с наличием противоположных интересов участников (экономических агентов). Кроме того, в обладающем инновационным потенциалом регионе, как правило, имеется большое количество направлений экономической деятельности и заинтересованных экономических агентов, учет которых приводит к значительному увеличению размерности исследуемых задач и повышает требования к качеству не только аналитического инструментария, но и инструментария автоматизированной обработки экономической информации.
В сложных системах к появлению синергетического эффекта, помимо временных факторов, могут приводить изменения различных параметров и их комплексов. В экономических системах с большим количеством элементов (экономические агенты, денежные потоки, основные производственные фонды (ОПФ), продукция и т.п.) и динамических связей между ними важно не только обнаружить синергетический эффект, но и объяснить его происхождение. В этой связи для выявления эффектов синергии целесообразно предварительно упростить исходные динамические модели. Применительно к моделированию региональных экономических систем, в работе [5] подробно описан основанный на применении z-оператора подход, позволяющий сводить многокритериальные многошаговые задачи линейного программирования к статическим задачам, сохраняющим качественные и некоторые количественные свойства исходных динамических моделей. На основе применения указанного подхода в [5] получены аналитические оценки значений переменных и критериев модели, а также их линейных сверток. Особенностью указанных моделей является подробный учет бухгалтерских правил формирования доходных и расходных потоков экономических агентов, в первую очередь, потоков прибыли и амортизации в производственной подсистеме, а также основных налоговых потоков в подсистеме управляющего органа. Обоснованные в работе [5] концепция, модели, методы анализа, а также разработанный на их основе автоматизированный программный комплекс «Карма» [1] легли в основу системы поддержки принятия решений [3] не только при управлении региональным экономическим развитием, но и при анализе социально-экономических систем различного уровня [4,6].
Целью данной работы является разработка статической, многокритериальной математической модели региональной социально-экономической системы и оценка на ее основе синергетического эффекта от использования ряда инновационных факторов.
Математическая модель
В работе [2] приведена построенная с использованием z-оператора математическая модель экономической системы, которую, в зависимости от степени агрегирования экономических показателей, можно использовать не только на мезоуровне, но и при описании деятельности производственного предприятия. Указанная модель представляет собой задачу линейного программирования, допускающую эффективный численный анализ симплекс-методом. Рассмотрим ее модификацию, представляющую собой двухкритериальную модель взаимодействия регионального производителя и управляющего (налогового) органа:
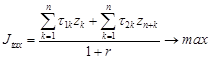 ;
;
![]() ;
;
![]() ; (1)
; (1)
![]() ;
;
![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
,
где k=1,…,n – порядковый номер ОПФ (направления экономической деятельности в регионе, производственного предприятия, отрасли и т.п.); n – количество ОПФ; mk – количество единиц k-го ОПФ; сk – стоимость k-го ОПФ; Pk – стоимость реализации продукции, произведенной на k-ом ОПФ; Vk – производительность k-го ОПФ; Tk – время полезного использования k-го ОПФ; T – горизонт планирования инвестиционного проекта; r – ставка дисконтирования на всем горизонте планирования; qk – спрос на продукцию, произведенную на k-ом ОПФ; ![]() – максимальная фондоотдача в единицу времени k-го ОПФ;
– максимальная фондоотдача в единицу времени k-го ОПФ; ![]() – экспертно задаваемый коэффициент, отражающий, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж k-го вида продукции; αi, i=1,…,4 – соответственно ставки налогов на добавленную стоимость, на имущество и на прибыль, а также страховых взносов регионального производственного сектора; p – средний процент оборотных затрат в регионе в сумме всех затрат регионального производственного сектора; β1 – средний процент выручки от продаж регионального производственного сектора, выделяемый на ФОТ; I0 – максимальная сумма дополнительных внутренних инвестиций в регион; K0 – максимальная сумма дополнительных внешних инвестиций в регион; M0 – максимальная сумма инвестиций в основные фонды региона;
– экспертно задаваемый коэффициент, отражающий, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж k-го вида продукции; αi, i=1,…,4 – соответственно ставки налогов на добавленную стоимость, на имущество и на прибыль, а также страховых взносов регионального производственного сектора; p – средний процент оборотных затрат в регионе в сумме всех затрат регионального производственного сектора; β1 – средний процент выручки от продаж регионального производственного сектора, выделяемый на ФОТ; I0 – максимальная сумма дополнительных внутренних инвестиций в регион; K0 – максимальная сумма дополнительных внешних инвестиций в регион; M0 – максимальная сумма инвестиций в основные фонды региона;
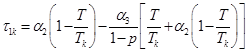 ,
,![]() ;
;
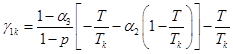 ,
, ![]() .
.
Переменные модели (1):
![]() – стоимость приобретаемых ОПФ k-го вида (инвестиции в основные фонды);
– стоимость приобретаемых ОПФ k-го вида (инвестиции в основные фонды); ![]() – выручка от продажи продукции (в количестве yk, стоимостью Pk), произведенной на k-м ОПФ; z2n+1 – сумма дополнительных инвестиций, внутренних для регионального производственного сектора; z2n+2 – сумма дополнительных инвестиций, внешних для регионального производственного сектора.
– выручка от продажи продукции (в количестве yk, стоимостью Pk), произведенной на k-м ОПФ; z2n+1 – сумма дополнительных инвестиций, внутренних для регионального производственного сектора; z2n+2 – сумма дополнительных инвестиций, внешних для регионального производственного сектора.
Предложенная математическая модель позволяет учитывать такие характерные для инновационного региона факторы, как неопределенность ценообразования, спроса, соотношение производственных затрат (общих, оборотных, на оплату труда, амортизации), влияние на параметры эффективности проекта периода послепродажного обслуживания инновационной продукции, налоговый потенциал и другие факторы. Данная модель является моделью региона, так как, кроме интересов производителя и налогового органа, в ней учтены также интересы потребителя (путем учета уровня оплаты труда, платежеспособного спроса, страховых взносов предприятий).
Целевые критерии Jtax, Jinv в (1) содержательно представляют собой сальдо денежных потоков соответственно управляющего органа (налоговые сборы) и производственного сектора региона (прибыль, инвестиции, производственные затраты), приведенных по ставке r, учитывающей требования инвесторов по доходности проекта, инфляционную составляющую, а также наличие других, характерных для региональных инновационных проектов рисков. Ограничения в (1) имеют следующий содержательный смысл, соответственно: первое – неотрицательность собственных средств (платежеспособность) регионального производственного сектора, второе – ограничение выпуска продукции технико-экономическими возможностями ОПФ с коэффициентом пропорциональности в виде их фондоотдачи, третье – ограничение выпуска уровнем спроса на продукцию, в том числе инновационную. Последняя группа неравенств отражает инвестиционные ограничения.
Синергетический эффект
Относительный синергетический эффект СЭ (как процентное приращение значений линейной свертки целевых критериев) от совместного влияния m однонаправленных параметров вычисляется по формуле:
СЭ = Cинт –![]() +m–1 (2)
+m–1 (2)
где Cинт – эффект от одновременного влияния параметров, Ck – эффект от влияния k-го параметра. Под эффектом от влияния параметров модели здесь имеется в виду коэффициент, пропорционально отражающий изменение значения целевого критерия в зависимости от изменения значений одного или нескольких параметров.
Результаты численных расчетов и их анализ
Предварительные расчеты, проведенные с помощью пакета «Карма», позволили сделать вывод о существовании решения в модели (1) в широком диапазоне изменения ее параметров. На рисунке приведены рассчитанные по формуле (2) значения синергетического эффекта для производственного сектора региона от изменения значений двух (m=2) модельно заданных параметров rps(1) и P1.
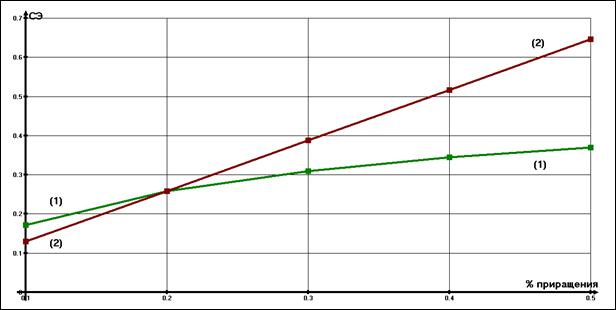
Рисунок. Зависимость синергетического эффекта от процента приращения параметров rps(1) (линия 1) и P1 (линия 2)
Предложенная методика позволяет определять величину синергетического эффекта, отражающего добавленную стоимость ИП в зависимости от приращения значений как инновационных, так и других, содержательно важных параметров.
Заключение
Таким образом, описанный выше подход к анализу региональных экономических систем требует обязательного наличия следующих составляющих: модель функционирования системы (как правило, многокритериальная); методы анализа модели, позволяющие получать аналитические решения или их оценки; автоматизированные средства обработки модельной информации с целью проведения численных экспериментов, расчета синергетического эффекта, установления оптимальных балансов потоков в ней.
Рецензенты:
Алексеев Дмитрий Валентинович, д.т.н., профессор, профессор кафедры вычислительной техники и информационных технологий Кемеровского института (филиала) Российского государственного торгово-экономического университета, г. Кемерово.
Зыков Виктор Семенович, д.т.н., профессор, заместитель директора по науке Института угля Сибирского отделения РАН, г. Кемерово.
Библиографическая ссылка
Медведев А.В. К ОЦЕНКЕ СИНЕРГЕТИЧЕСКОГО ЭФФЕКТА В МОДЕЛИ РЕГИОНА С ИННОВАЦИОННЫМИ ФАКТОРАМИ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8201 (дата обращения: 09.03.2026).



