При построении математических моделей нередко возникают случаи, когда некоторые входные величины не определены и найти их численные значения не представляется возможным. Существует несколько подходов к раскрытию неопределенностей.
Известно несколько подходов к раскрытию неопределенностей. Широко используется вероятностный подход [1], в котором неопределенные параметры характеризуются функциями плотности распределения. Математические модели, в состав которых входят такие параметры, имеют названия вероятностных. В этом случае функции распределения строятся на основании накопленных статистических данных о поведении стохастических параметров. Трудность применяемой методики связана с необходимостью проведения большого числа экспериментов на объекте во время хода технологического процесса для определения параметров законов распределения стохастических величин.
Другой подход связан с использованием теории нечетких множеств [4] и уходит в сферу субъективной информации. Неопределенные параметры характеризуются функциями принадлежности, которые строятся на основе опросов экспертов. Модели, в которых неопределенные параметры характеризуются функциями принадлежности, получили название нечетких математических моделей. Недостатком этой методики является то, что для надежного построения функции принадлежности требуется мнение нескольких экспертов. Это не всегда возможно.
На практике чаще всего информация о значении неопределенного параметра ![]() задается в виде интервального параметра [2] (интервального числа):
задается в виде интервального параметра [2] (интервального числа):
![]() ,
,![]()
где ![]() – нижняя и верхняя граница параметра
– нижняя и верхняя граница параметра ![]() ;
; ![]() – середина интервала
– середина интервала ![]() (рис. 1):
(рис. 1):
![]() ; (1)
; (1)
величина ![]() – есть интервал, который определяется:
– есть интервал, который определяется:
![]() . (2)
. (2)
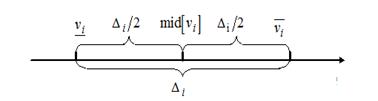
Рис. 1. Изображение интервального параметра ![]() на числовой прямой.
на числовой прямой.
Рассмотрим интервальную теорию на примере класса статических математических моделей с распределенными параметрами [5], которые определяются уравнениями вида:
![]()
![]() , (3)
, (3)
где z – пространственная координата объекта.
На первом этапе исследования зависимости ![]() ,
, ![]()
![]()
![]() определяется правило вычисления границ
определяется правило вычисления границ ![]() . В процессе исследования (рис. 2) для каждого
. В процессе исследования (рис. 2) для каждого ![]()
![]() строятся зависимости
строятся зависимости ![]() .
.
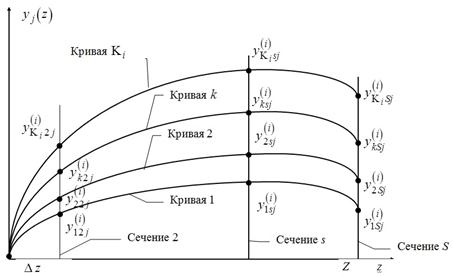
Рис. 2. Построение последовательностей ![]() при исследовании зависимости
при исследовании зависимости ![]() .
.
Далее по пространственной координате z объекта с шагом ![]() определяются точки
определяются точки ![]() . В результате образуются последовательности:
. В результате образуются последовательности:
![]() ,...,
,...,![]() , ... ,
, ... ,
![]() , (4)
, (4)
где первый подстрочный индекс означает номер кривой (на рис. 2 кривая ![]() обозначается как кривая 1, кривая 2, ..., кривая k, ...,); второй подстрочный индекс соответствует номеру линии, обозначаемой как сечение s
обозначается как кривая 1, кривая 2, ..., кривая k, ...,); второй подстрочный индекс соответствует номеру линии, обозначаемой как сечение s![]() , на которой лежит точка
, на которой лежит точка ![]() ; третий индекс соответствует номеру выходного параметра
; третий индекс соответствует номеру выходного параметра ![]() .
.
Если для заданного i все S последовательностей (4) являются монотонными, тогда ![]() (рис. 3а). В этом случае нижние и верхние границы определяются соответственно:
(рис. 3а). В этом случае нижние и верхние границы определяются соответственно:
![]() , (5)
, (5)
![]() . (6)
. (6)
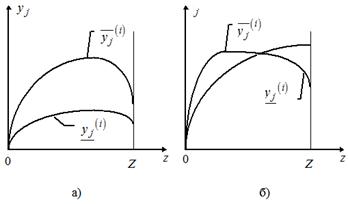
Рис. 3. К определению границ интервала ![]() для зависимости
для зависимости ![]() при
при ![]() (а); при
(а); при ![]() (б).
(б).
Если хотя бы одна из s![]() последовательностей является немонотонной, тогда
последовательностей является немонотонной, тогда ![]() (рис. 3б).
(рис. 3б).
На втором этапе определяется значимость интервала ![]() для выходной переменной
для выходной переменной ![]() , согласно неравенству:
, согласно неравенству:
![]() . (7)
. (7)
Здесь ![]()
![]() определяются из (14-5), (15-6), если
определяются из (14-5), (15-6), если ![]() . В противном случае из решений задач оптимизации
. В противном случае из решений задач оптимизации ![]() ,
, ![]() .
.
Если условие (7) не выполняется, то интервал ![]() для
для ![]() считается незначимым и при определении
считается незначимым и при определении ![]() ,
, ![]() задается в виде точки со значением
задается в виде точки со значением ![]()
![]() .
.
После проведенных исследований интервальный выходной параметр ![]() определяется по формуле:
определяется по формуле:
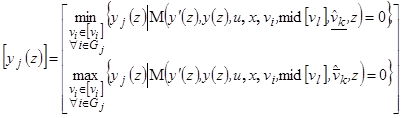 , (8)
, (8)
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Таким образом, представленная методика позволяет найти выходные параметры интервальной модели, которые определяются верхней и нижней границей выходного параметра.
Данная методика реализована на примере процесса обжига во вращающейся печи. Вращающаяся печь – это промышленная печь цилиндрической формы с вращательным движением вокруг продольной оси, предназначенная для нагрева материалов с целью их физико-химической обработки. Для поддержания температурного режима применяется факельное сжигание природного газа. Материал в печи движется противотоком продуктам сгорания [3].
Нами разработана математическая модель процесса обжига во вращающейся печи [6]:
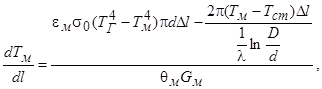 (9)
(9)
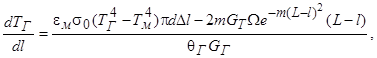 (10)
(10)
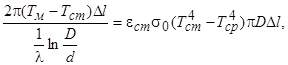 (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
где ![]() – температура материала [K],
– температура материала [K], ![]() – температура газа [K],
– температура газа [K], ![]() – температура стенки [K],
– температура стенки [K], ![]() – температура среды [K],
– температура среды [K], ![]() – текущая длина печи [м],
– текущая длина печи [м], ![]() – степень черноты футеровки,
– степень черноты футеровки, ![]() – степень черноты материала,
– степень черноты материала, ![]() – внутренний диаметр печи [м],
– внутренний диаметр печи [м], ![]() – внешний диаметр печи [м],
– внешний диаметр печи [м], ![]() – общая длина печи [м],
– общая длина печи [м], ![]() – коэффициент излучения абсолютно черного тела [Вт/м2К4],
– коэффициент излучения абсолютно черного тела [Вт/м2К4], ![]() – коэффициент теплопроводности материала футеровки [Вт/мК],
– коэффициент теплопроводности материала футеровки [Вт/мК], ![]() – тепло, выделяющееся от сгорания 1 кг топлива (удельная теплота сгорания) [Дж/кг],
– тепло, выделяющееся от сгорания 1 кг топлива (удельная теплота сгорания) [Дж/кг], ![]() – теплоемкость материала [Дж/кг
– теплоемкость материала [Дж/кг![]() ],
], ![]() – теплоемкость газа [Дж/кг
– теплоемкость газа [Дж/кг![]() ],
], ![]() – расход материала [кг/с],
– расход материала [кг/с], ![]() – расход газа [
– расход газа [![]() /с],
/с], ![]() – расход топлива [
– расход топлива [![]() /с],
/с], ![]() – эмпирический коэффициент.
– эмпирический коэффициент.
В данной математической модели есть неопределенные параметры, численные значения которых изначально неизвестны. Это степень черноты материала ![]() , теплоемкость материала
, теплоемкость материала ![]() и длина факела
и длина факела ![]() . Эмпирический коэффициент
. Эмпирический коэффициент ![]() зависит от длины факела, следовательно, изменение длины факела влечет за собой изменение данного эмпирического коэффициента.
зависит от длины факела, следовательно, изменение длины факела влечет за собой изменение данного эмпирического коэффициента.
Математическая модель процесса обжига во вращающейся печи относится к классу статических моделей с распределенными параметрами.
Для успешного ведения технологического процесса необходимо обеспечить заданную температуру материала в определенных точках в каждой печи. В условиях неопределенности параметров математической модели постановка задачи обеспечения заданного технологического режима формулируется следующим образом: для заданных условий окружающей среды ![]() , производительности установки
, производительности установки ![]() необходимо найти расход топлива
необходимо найти расход топлива ![]() , при которых достигается выполнение технологических условий производства, т.е. интервал значения температуры на заданной длине печи должен быть подмножеством интервала температуры, заданного технологом:
, при которых достигается выполнение технологических условий производства, т.е. интервал значения температуры на заданной длине печи должен быть подмножеством интервала температуры, заданного технологом:
![]()
На первом этапе необходимо задать границы интервалов для неопределенных параметров: ![]() =[0.3, 0.7];
=[0.3, 0.7]; ![]() =[1000, 1200];
=[1000, 1200]; ![]() =[7, 15]. В данных математических моделях выходными параметрами являются распределение температур газа, материала и стенки по длине печи, но наиболее важный параметр для процесса обжига – это температура материала, следовательно, все расчеты проведем только для температуры материала.
=[7, 15]. В данных математических моделях выходными параметрами являются распределение температур газа, материала и стенки по длине печи, но наиболее важный параметр для процесса обжига – это температура материала, следовательно, все расчеты проведем только для температуры материала.
Далее необходимо построить последовательности (4). Строится график зависимости степени черноты материала равной 0.3 от всех остальных интервальных величин, и из них находим верхнюю и нижнюю границу (рис. 4).
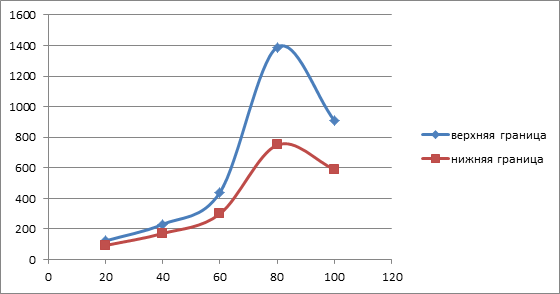
Рис. 4. ![]() для
для ![]() =0.3.
=0.3.
Аналогично строим зависимости для ![]() =0.4;
=0.4; ![]() =0.5;
=0.5; ![]() =0.6;
=0.6; ![]() =0.7.
=0.7.
После проведенных исследований находим верхнюю и нижнюю границу для всего интервала ![]() (рис. 5).
(рис. 5).
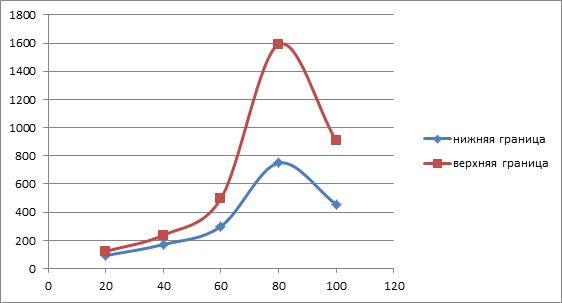
Рис. 5. Границы интервала ![]() для противотока.
для противотока.
Как видно из рис. 5, распределение температуры материала находится в области между верхней и нижней границами.
Далее определяется значимость интервала ![]() для выходной переменной, согласно неравенству (7). Параметр
для выходной переменной, согласно неравенству (7). Параметр ![]() – это допустимая погрешность, значение которой задается технологом. В данном случае погрешность составляет 3
– это допустимая погрешность, значение которой задается технологом. В данном случае погрешность составляет 3![]() . Как видно из рис. 9, интервал
. Как видно из рис. 9, интервал ![]() является значимым.
является значимым.
Следовательно, данная методика позволяет гарантированно вычислять интервал выходных значений математических моделей, что дает преимущества перед другими способами раскрытия неопределенностей в математических моделях.
Рецензенты:
Туголуков Евгений Николаевич, д.т.н., профессор кафедры «Техника и технологии производства нанопродуктов» ФГБОУ ВПО «Тамбовский государственный технический университет», г. Тамбов.
Борщев Вячеслав Яковлевич, д.т.н., профессор, зав. кафедрой «Техносферная безопасность» ФГБОУ ВПО «Тамбовский государственный технический университет», г. Тамбов.
Библиографическая ссылка
Туляков Д.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОБЖИГА ВО ВРАЩАЮЩЕЙСЯ ПЕЧИ В УСЛОВИЯХ ИНТЕРВАЛЬНОЙ НЕОПРЕДЕЛЕННОСТИ ИСХОДНЫХ ДАННЫХ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8150 (дата обращения: 09.03.2026).



