Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Денисов А.В. 1 Треков А.Г. 1 Митяшин Н.П. 1

---

1 ФГБОУ ВПО “Саратовский государственный технический университет имени Гагарина Ю. А.”

Предлагается методика представления в реальном масштабе времени состояния преобразовательного комплекса (ПК) с целью распознавания причин снижения качества генерируемой им электроэнергии. Методика основана на автоматическом наблюдении за характером изменения токов и напряжений на выбранных элементах силовой схемы и сравнении наблюдаемых сигналов с заранее накопленными законами изменения этих сигналов для основных видов неисправностей. Для автоматизации распознавания типа неисправности использован аппарат контурного анализа. Реализация предлагаемой методики позволит в реальном масштабе времени контролировать качество электрической энергии, генерируемой ПК, и выявлять наиболее вероятные причины его снижения. Дальнейшие перспективы проекта – распространение методики на другие предметные области, поскольку разработанная методика является универсальной и может представлять интерес для специалистов различных областей техники.

Статья в формате PDF

143 KB

деградация.

аварийные и предаварийные режимы

показатели качества электроэнергии

преобразовательный комплекс

контурный анализ

1. Введение в контурный анализ / Под ред. Я. А. Фурмана. – М.: ФИЗМАТЛИТ, 2003. – 592 с.

2. Денисов А. В., Митяшин Н. П. Некоторые алгоритмы сведения многокритериальных задач к однокритериальным. // Анализ, синтез и управление в сложных системах: Сборник научных трудов. – Саратов: СГТУ, 2010. – С.85-91.

3. Денисов А. В., Паранькина А. С. Моделирование причинно-следственных связей в задачах повышения качества электроэнергии, генерируемой преобразователем частоты // Научно-технический журнал Вестник СГТУ №4(51). – Вып. 3. – Саратов: СГТУ, 2010. – С.172-176.

4. Денисов А. В., Халистова В. А., Смольков М., Федосеева М. Графические образы неисправностей в схемах вентильных преобразователей // ММТТ – 24 – Математические методы в технике и технологиях: сборник трудов конференции молодых ученых и студентов СГТУ. – Саратов: СГТУ, 2011. – С.57-58.

5. Митяшин Н. П. Агрегированные преобразовательные комплексы для питания цеховой двигательной нагрузки на частотах, отличных от общепромышленной: дисс… д-ра техн. наук. – Саратов, 2003. – 450 с.

Введение

Проблема качества электроэнергии и пути ее решения в данный момент обусловлены возросшим распространением новых видов нагрузок и источников, в частности, вентильных преобразователей и комплексов. Последние, являясь генераторами высших гармоник, вносят значительные искажения в форму кривой напряжения. Те меры, которые предпринимаются для устранения этих недостатков в номинальных режимах, оказываются неэффективными в случаях выхода из строя элементов, предусмотренных для реализации этих мер, хотя это и не приводит к нарушению общей работоспособности (деградация ПК). Такие режимы ПК назовем предаварийными.

Цель исследования

Таким образом, в настоящее время все большую практическую ценность приобретают разработки, направленные на улучшение показателей качества электрической энергии в электрических комплексах и предотвращение их ухудшения [5]. Целью настоящей работы является создание методики представления образа состояния ПК с целью автоматического обнаружения типичных предаварийных и аварийных режимов их работы.

Методика исследования

Для автоматизации распознавания типа неисправности в ПК может быть использован аппарат контурного анализа (далее КА) [1]. В традиционном применении КА применяется для описания, хранения, сравнения и поиска объектов, представленных в виде плоских замкнутых кривых без пересечений – контуров. При этом имеется в виду, что непрерывная кривая в компьютерном представлении моделируется последовательностью точек экрана – пикселов. Приведенные ниже формулы КА могут применяться в задаче распознавания неисправностей в ПК. При этом под термином «контур» нами понимается не визуальный образ, а вектор мгновенных значений наблюдаемого или образцового для некоторого предаварийного режима процесса. Сохранение этого термина связано с тем, что он употребляется в применяемом нами аппарате контурного анализа.

В КА контур кодируется последовательностью комплексных чисел. На контуре фиксируется точка, которая называется начальной. Затем, контур обходится, и каждый вектор смещения записывается комплексным числом a+ib. Здесь действительная часть кода а – смещение точки по оси X, a мнимая b – смещение по оси Y относительно предыдущей точки.

Таким образом, контур описывается последовательностью комплексных чисел

,

где n – количество точек в пиксельной модели кривой, которое будем считать фиксированным. Для целей распознавания необходимо ввести метрику, характеризующую степень совпадения (близость) двух контуров. Для этой цели вводятся скалярное произведение и нормированное скалярное произведение контуров. Пусть – контур той же размерности, что и контур . Тогда скалярное произведение этих контуров задается формулой

.

Таким образом, скалярное произведение контуров есть комплексное число, действительная часть которого является обычным скалярным произведением евклидовых векторов с соответствующими координатами.

Нормированное скалярное произведение (НСП) задается формулой

,

где и – нормы контуров, вычисляемые по формуле

.

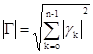Нормированное скалярное произведение (НСП) может служить мерой близости контуров благодаря следующему свойству: есть комплексное число, для которого

,

причем равенство здесь выполняется тогда и только тогда, когда контуры и отличаются лишь поворотом и масштабом, независимо от того, где они находятся. Это означает, что равенство равносильно равенству

,

где – некоторое комплексное число, определяющее масштаб и угол между контурами. При этом действительная часть дает косинус этого угла.

Если же модуль меньше единицы, то это свидетельствует о несовпадении форм контуров, причем меньшая величина соответствует их большему различию.

Равенство для совпадающих по форме контуров имеет место лишь в том случае, если в качестве начальных точек последовательностей и рассматривается одна и та же точка контура.

Обозначим теперь через n число распознаваемых неисправностей, а через m – число наблюдаемых процессов в преобразователе. Пусть – характерный контур i-го наблюдаемого процесса, соответствующий k-й неисправности, а – контур i-го наблюдаемого процесса в предъявляемом к распознаванию режиме работы преобразователя. Полные наборы этих контуров образуют m-мерные векторы [3, 4]:

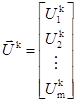и .

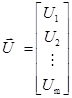Близость векторов и может служить оценкой возможности распознавания предъявленного режима как k-й неисправности. Эту близость векторов можно выразить через определяемые описанным выше алгоритмом степени совпадения формы контуров и , т.е. через величины , следующим образом

.

Здесь – наборы весовых коэффициентов, характеризующих важность формы кривой i-го наблюдаемого процесса для распознавания k-й неисправности. Коэффициенты определяются экспертами, например, по методике, предложенной в [2]. При этом весовые коэффициенты должны быть нормированы, т.е.

, (1)

что обеспечивает выполнение равенства при полном совпадении и .

Кодирование сигналов для контурного анализа

В результате моделирования или снятия сигнала с действующей установки формируется текстовый файл заданного объема, который можно представить в виде таблицы или кортежа

Здесь N – число значений кодируемого образа, i – порядковый номер значения, и – соответствующие момент времени и значение сигнала, причем .

Для правильного отображения сигнала в виде контура необходимо, чтобы моменты времени фиксации сигнала были равноотстоящими, т.е. , где h – фиксированная величина.

Поскольку кодируемый сигнал предполагается периодическим с периодом T, то будем считать, что .

Для улучшения наглядности целесообразно перейти от исходного массива к его полярной интерпретации, для чего воспользуемся формулами

; ; .

В результате формируется кортеж

Пусть и – минимальное и максимальное значения из третьего столбца, а и – минимальное и максимальное значения из четвертого столбца.

Исходя из сложности формы сигнала, выбираем количество дискретизаций по осям x и y. Эти значения и влияют на точность аппроксимации формы сигнала: чем больше их величина, тем точнее представление формы кодом в контурном анализе.

Положим

;

Для завершения кодирования достаточно положить

, (2)

, причем полагаем

Здесь – функция округления до ближайшего целого, т.к. по определению компоненты кода контурного анализа целые числа.

Поскольку каждое округление приводит к накапливаемой погрешности, то расчеты по последним формулам рекомендуется сопровождать следующей корректирующей процедурой.

После каждого округления следует накапливать текущие погрешности ипо формулам:

При достижении величинами и значений и следует осуществлять коррекцию, заменяя на следующем шаге формулы (2) для расчета величин и формулами:

и (3)

Результат кодирования теперь можно представить кортежем:

(4)

Ниже представлены результаты работы программы, в которой реализован аппарат контурного анализа.

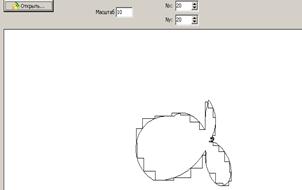
Рис.1. Визуализация результатов кодирования кривых с помощью контурного анализа

На рис.1 слева изображена экранная форма, на которой представлена кривая тока источника питания (слева) и кривая выходного напряжения (справа) при моделировании исчезновения импульса управления одного из тиристоров в трехфазном мостовом параллельном инверторе тока.

В результате получаем код кривой в табличном виде:

Таблица 1. Фрагмент результатов кодирования сигнала по полученной формуле (4) при моделировании обрыва тиристора или исчезновении импульса управления тиристором. В таблице 1 выделен интервал из 10 точек (от т.19 до т.29) из общего интервала в 360 точек, на рис.1 – интервал между т. А и т. B (на изображении слева)

Прогнозируемый результат исследования

Реализация предлагаемой методики позволит в реальном масштабе времени контролировать качество электрической энергии, генерируемой ПК, и выявлять наиболее вероятные причины его снижения.

Заключение

Научная и практическая новизна заключается в разработке оригинальной методики представления информации о текущем состоянии ПК и предпосылке создания на ее основе системы распознавания предаварийных режимов работы.

Дальнейшие перспективы проекта – распространение методики на другие предметные области, поскольку разработанная методика является универсальной и может представлять интерес для специалистов различных областей техники.

Рецензенты:

Угаров Геннадий Григорьевич, доктор технических наук, профессор, профессор кафедры «Электроснабжение промышленных предприятий» СГТУ имени Гагарина Ю. А., г. Саратов.

Львов Алексей Арленович, доктор технических наук, профессор, заведующий кафедрой «Техническая кибернетика и информатика» СГТУ имени Гагарина Ю. А., г. Саратов.

Библиографическая ссылка