Введение
В настоящее время для задач автоматического управления и обработки сигналов широко применяются цифровые модели непрерывных систем. Основным элементом таких систем является цифровой интегратор: традиционно для его реализации используется математический аппарат, известный как z-преобразование [3]. Применение z‑преобразования обнаруживает серьезный недостаток: при высокой частоте дискретизации корни и полюса системы в z-области стремятся к единице. Это существенно затрудняет работу с такими функциями на устройствах, не поддерживающих операции с плавающей точкой на аппаратном уровне. К ним относятся, прежде всего, 8- и 16‑битные микроконтроллеры. В настоящее время их доля на мировом рынке составляет около 70 %, и это соотношение сохранится в течение ближайших лет [4]. Стоит отметить, что операции с плавающей точкой не поддерживают аппаратно и многие 32-битные устройства, в частности, поостренные на базе процессорных ядер Cortex M0 и Cortex M3. В свете этого представляется актуальной задача поиска эффективного способа описания цифровых систем при ограниченной разрядной сетке.
Альтернативой z-преобразованию, свободной от его недостатков, является т.н. дельта-преобразование (delta transform). Оно достаточно детально описано в работах Мидлтона и Гудвина (Middleton and Goodwin, 1980-е гг.), но по сей день остается малоизвестным способом перехода от непрерывных систем к дискретным.
Определение дельта-преобразования
В основе дельта-преобразования лежит известная операция численного дифференцирования первого порядка:
![]() (1)
(1)
Символом ![]() в данном случае обозначен период дискретизации. В качестве переменной вместо
в данном случае обозначен период дискретизации. В качестве переменной вместо ![]() введем
введем ![]() , которая имеет следующий смысл:
, которая имеет следующий смысл:
![]() , (2)
, (2)
где ![]() – значение сигнала в
– значение сигнала в ![]() -й момент времени.
-й момент времени.
Как известно [3], суть z-преобразования состоит в переходе от операции дифференцирования к операции сдвига во времени. Переменная ![]() при этом обозначает сдвиг во времени на 1 шаг вперед:
при этом обозначает сдвиг во времени на 1 шаг вперед: ![]() . (3)
. (3)
Исходя из (2) и (3), нетрудно выяснить связь между переменными ![]() и
и ![]() :
:
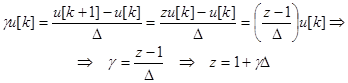 (4)
(4)
Напомним, что связь между переменными ![]() и
и ![]() такова:
такова: ![]() (5)
(5)
Из формулы (4) найдем связь между оператором сдвига ![]() и переменной
и переменной ![]() :
:
![]() (6)
(6)
Одним из наиболее употребительных способов перехода из преобразования Лапласа в z-преобразование является так называемое билинейное преобразование, или подстановка Тастина (приближенное), основанное на замене: ![]() (7)
(7)
Обратное преобразование Тастина основано на обратной замене: 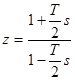 (8)
(8)
Дискретизированная таким образом система сохраняет устойчивость, если исходная система была устойчива, что делает преобразование Тастина наиболее популярным способом перехода к дискретной системе. При переходе от z-преобразования к дельта-преобразованию также можно использовать преобразование Тастина. При этом связь между переменной ![]() и
и ![]() такова:
такова: 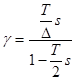 (9)
(9)
Фундаментальное отличие дельта-системы от z-системы заключается в том, что при уменьшении периода дискретизации дельта-система стремится к непрерывной системе, в то время как в z-системе этого не происходит. Рассмотрим поведение корней характеристического полинома при стремлении ![]() :
:
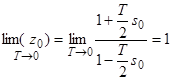 , (10)
, (10)
тогда как, если принять, что ![]() :
: 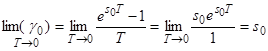 (11)
(11)
Таким образом, корни характеристического полинома z-системы при ![]() стремятся к единице, в то время как корни характеристического полинома дельта-системы стремятся к корням исходной системы. Это свойство с чисто математической точки зрения не дает никаких преимуществ дельта-преобразованию по сравнению с z-преобразованием. Но все меняется, когда мы имеем дело с ограниченной точностью представления данных на вычислительной машине.
стремятся к единице, в то время как корни характеристического полинома дельта-системы стремятся к корням исходной системы. Это свойство с чисто математической точки зрения не дает никаких преимуществ дельта-преобразованию по сравнению с z-преобразованием. Но все меняется, когда мы имеем дело с ограниченной точностью представления данных на вычислительной машине.
Моделирование цифрового интегратора
Так как интегратор является базовым элементом практически любой системы управления [2], то исследование свойств цифрового интегратора на основе дельта-преобразования представляет несомненный интерес.
Для исследования эффекта квантования по уровню коэффициентов передаточных функций нами была разработана модель двухточечного интегратора. Стоит отметить, что использование большего числа точек интегрирования увеличивает задержку в системе, что нежелательно. Рассмотрим в сравнении две модели интегратора: на основе z-преобразования и дельта-преобразования.
Интегратор на основе z-преобразования строится на основе метода трапеций, как наиболее точного из двухточечных. Итерационная формула для вычисления значения интеграла такова:
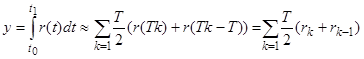 , (12)
, (12)
где ![]() – период дискретизации. Отсюда следует итерационная формула:
– период дискретизации. Отсюда следует итерационная формула:
![]() (13)
(13)
Перепишем это выражение с использованием оператора сдвига ![]() :
:
![]() (14)
(14)
Интегратор на основе дельта-преобразования может быть выведен из формулы (4). В самом деле:
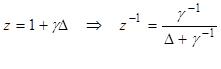 (15)
(15)
Подставим эту замену в формулу (14):
![]() (16)
(16)
Обозначим: ![]() (17)
(17)
Из (2) и (17) следует: ![]() (18)
(18)
На основе (16) и (18) легко записать итоговую систему равенств для интегратора на основе дельта-преобразования, построенного по методу трапеций:
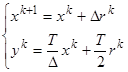 (19)
(19)
Обратим внимание: хотя при выводе выражения (11) предполагалось, что ![]() , но на практике мы можем выбирать значение
, но на практике мы можем выбирать значение ![]() , отличное от
, отличное от ![]() . С помощью подбора
. С помощью подбора ![]() можно добиться повышения точности вычислений (фактически,
можно добиться повышения точности вычислений (фактически, ![]() играет роль масштабирующего коэффициента) [5]. Подбор
играет роль масштабирующего коэффициента) [5]. Подбор ![]() – нетривиальная задача оптимизации.
– нетривиальная задача оптимизации.
В среде LabVIEW было проведено моделирование цифровых интеграторов, построенных на основе z-преобразования и дельта-преобразования. В качестве входного сигнала была взята синусоида с периодом ![]() и амплитудой 1, период дискретизации в системе был принят равным
и амплитудой 1, период дискретизации в системе был принят равным ![]() . Параметр
. Параметр ![]() (подобран экспериментально). Было создано две модели: для длины слова 16 бит и 32 бита.
(подобран экспериментально). Было создано две модели: для длины слова 16 бит и 32 бита.
Моделирование 16-битного интегратора
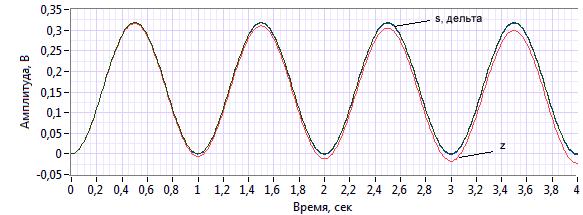
Рисунок 1. Реакция на синусоидальное воздействие 16-битного интегратора
Из рисунка 1 видно, что при 16-битной длине слова z-интегратор накапливает ошибку значительно быстрее, чем дельта-интегратор. Более детально это можно видеть на графике ошибки.
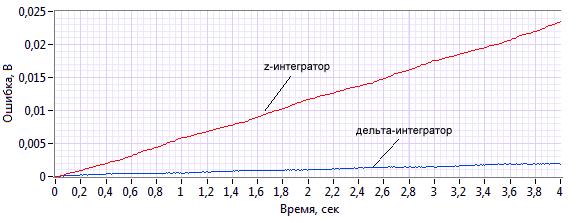
Рисунок 2. Ошибка 16-битного интегратора в различных реализациях
Данные линии визуально кажутся прямыми, хотя известно, что для синусоидального сигнала ошибка интегратора по методу трапеций должна повторять гармонику. При увеличении масштаба становится видно, что в данном случае это правило не нарушается (рис. 3). Внешний вид погрешности обусловлен наличием инструментальной составляющей.
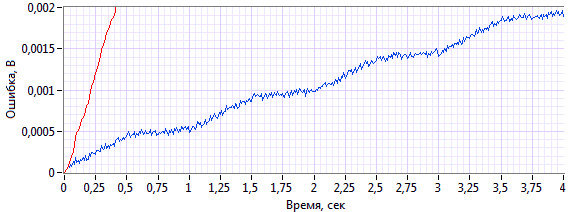
Рисунок 3. Ошибка 16-битного интегратора на основе дельта-преобразования (возрастающая синусоида)
Пилообразный шум возникает из-за ошибки округления [1]. Из приведенных графиков видно, что за 4 секунды работы накопленная ошибка 16-битного z-интегратора более чем на порядок превосходит ошибку дельта-интегратора.
Моделирование 32-битного интегратора
Ниже представлен график ошибки 32-битного интегратора для двух реализаций интегратора.
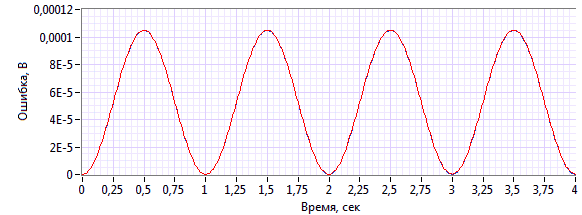
Рисунок 4. Ошибка 32-битного интегратора
На этом графике разница между ошибками z-интегратора и дельта-интегратора неразличима. Однако, сравнивая с ошибкой 16-битного интегратора (рисунок 2), видно: она меньше всего лишь на порядок для дельта-преобразования. Очевидно, что, увеличивая разрядность контроллера до 32-х бит, было бы целесообразно получить и значительно лучшую точность. Изменим условия эксперимента. Примем период дискретизации ![]() , а параметр
, а параметр ![]()
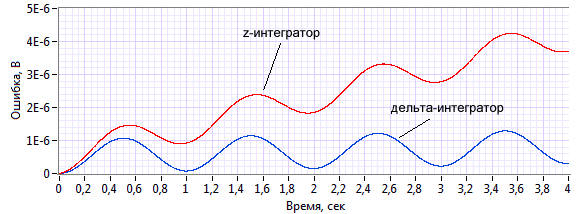
Рисунок 5. Ошибка 32-битного интегратора в различных реализациях
при периоде дискретизации ![]()
На графике (рисунок 5) видно, что накопленная ошибка z-интегратора растет значительно быстрее, чем ошибка дельта-интегратора.
Из сравнения графиков на рисунках 2 и 5 можно вывести следующую грубую оценку:
- при длине слова 16 бит накопленная ошибка z-интегратора достигает 0,025 (7,5 %) за 4 секунды. За это же время ошибка дельта-интегратора не превышает 0,002 (0,6 %);
- при длине слова 32 бит накопленная ошибка достигает ![]() (0,01 %) за 4 секунды. За это же время ошибка дельта-интегратора не превышает
(0,01 %) за 4 секунды. За это же время ошибка дельта-интегратора не превышает ![]() (0,001 %).
(0,001 %).
Заключение
Показано преимущество использования дельта-преобразования перед z-преобразованием при реализации цифрового интегратора в случае представления чисел с фиксированной точкой при ограниченной длине машинного слова, что позволяет увеличить точность численного интегрирования. Это правило верно как для 16-битного, так и для 32-битного представления чисел с фиксированной точкой, свойственного подавляющему большинству современных микроконтроллеров и цифровых сигнальных процессоров. По этой причине представляется оправданным отдавать предпочтение дельта-преобразованию при реализации цифровых систем.
Работа выполнена при поддержке Министерства образования и науки РФ в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009–2013 годы» (Государственный контракт № 14.B37.21.2021 от 11 ноября 2012 г.).
Рецензенты:
Куприянов Михаил Степанович, д.т.н., профессор кафедры вычислительной техники. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Фахми Шакиб Субхиевич, д.т.н., доцент кафедры систем автоматизированного проектирования. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Библиографическая ссылка
Каримов А.И., Бутусов Д.Н., Платонов С.М., Лавров С.В., Мандра А.Г. РЕАЛИЗАЦИЯ ЦИФРОВОГО ИНТЕГРАТОРА С ПРИМЕНЕНИЕМ ДЕЛЬТА-ПРЕОБРАЗОВАНИЯ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8130 (дата обращения: 09.03.2026).



