Нефть является важнейшим стратегическим сырьём, это неотъемлемый продукт производственного и хозяйственного процессов. Будучи одним из популярных сырьевых товаров, нефть торгуется на рынке динамичном и ликвидном, отягощённым событийными составляющими, цикличностью, сезонностью, статистическим «шумом» [5]. С момента открытия нефти во второй половине XIX-го века мировая нефтяная промышленность пережила не менее 8 циклических периодов активности. Пики сопровождались резкими и неизбежными спадами. Нефтяная отрасль представляет типичный пример boom/bust-бизнеса, для него характерны периоды лихорадочной активности, чередующиеся с временами застоя.
Цель исследования и постановка задачи
Мировой нефтяной рынок интересно представить в виде макроэкономического «поля», «игроки» на котором ограничены сверху двумя ресурсами - потенциальной ёмкостью мировой экономики и мощностью мировой нефтедобычи. В рамках этих двух лимитов они стараются наилучшим образом решить политические, социальные и экономические проблемы своих стран. Россия, будучи одной из сырьевых стран мира, свои макроэкономические показатели привязала к мировой цене нефти (и газа). Хотелось бы новыми экономико-математическими способами найти научно, аналитически, графически и численно зависимость её макроэкономических архетипов - ВВП и инфляции - от мировой цены нефти.
Полиформные модели в макроэкономике
Поскольку исходная информация представляется в виде таблиц, то её графики будут «решётчатыми» функциями с заданием множества кортежей длины два, где первая компонента кортежа соответствует году, вторая - исходному параметру (цене нефти, инфляции, объёму ВВП). В [8] было предложено два вида экономико-математических моделей при «решётчатой» структуре показателя - дискретная полиформная (конечные разности, исчисление сумм и пр.), непрерывная полиформная (гладкая кривая с аналитикой, производными и пр.). Часто традиционно соединяют точки «решётчатого» графика отрезками прямых. Математически это сплайн первого порядка, свойства которого можно полезно использовать. Но при этом уже первая производная терпит конечный разрыв, что соответствует разрыву тенденции, хотя ещё в 1890 году А. Маршалл в книге "Principles of Economics, an Introductory Volume" кратко предупреждал "Natura non facit salturn" - «Природа не делает скачков».
Определим надобность в «полиформных» моделях. На разных временных отрезках поведение макроэкономического показателя часто встречается с меняющимися условиями «экономической игры», в экономическом законодательстве разных стран варьируются правила, нормы, налоги, таксы, ставки, таможенные тарифы, акцизы, квоты, отчисления, преференции, субсидии, наценки и т.д. В [4] замечено: «... экономическая система имеет то свойство, что при поступлении внешней информации её параметры способны динамично меняться»; «... необоснованное вмешательство государства быстро разрушает экономическую систему». Поэтому искомый математический конструкт должен наилучшим образом анализировать «рваный» характер исходных причин динамики экономических показателей [5]. В этом случае макроэкономическое движение представляется моделью, состоящей из последовательно связанных во времени фрагментов, вот она-то и называется полиформной [8].
Ранее использовались непрерывные моноформные модели, но в современной экономике на разных темпоральных участках из-за смены «правил игры» придётся менять аппроксимирующие полиномы. Появившиеся «куски» разных полиномов надо будет «сшивать» на границах временных интервалов, в том числе и производными, каждый раз изобретая оптимальные способы преобразования «кусочного» образа макроэкономической временной зависимости в непрерывную аналитическую функцию с аналитическими же производными.
Сплайн-аппроксимация макроэкономических конъюнктур
Естественным выходом из этой ситуации становится применение теории сплайнов - математического конструкта, представляющего непрерывно «кусочную» структуру входного сигнала в полиформной модели (рис. 1, 2, 3). Математически «сшивка» фрагментов сплайна осуществляется значениями функции SPL(Y;Xj-0)=SPL(Y; Xj+0)=Yj слева и справа от каждого «узла» j=1..N «решётчатой» последовательности, а также значениями её первой, второй т.д. производных SPL1D(Y;Xj-0)=SPL1D(Y;Xj+0), SPL2D(Y;Xj-0)=SPL2D(Y;Xj+0) ... По всей длине интервале [E, F] проходящие через «узлы» «сетки» {áXj;Yjñ}, j=1..N функции SPL(Y;X), SPL1D(Y;X), SPL2D(Y;X) ... становятся непрерывными аппроксимирующими ансамблями.
|
|
|
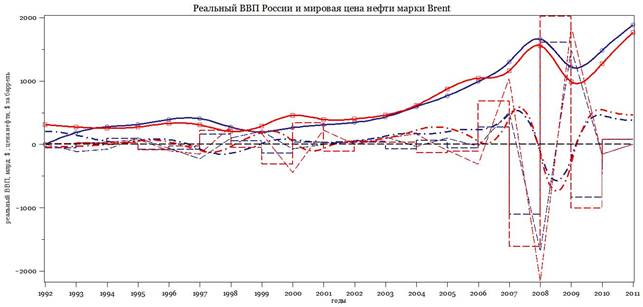
Рисунок 1 - Зависимости от времени объёма реального ВВП России (NAVY) и мировой цены марки Brent (RED) в 1992-2011 гг. Сплайн-модели. Первые производные (гладкие) - штрих-пунктир, вторые (треугольные) и третьи (прямоугольные) - пунктир. ВВП в млрд. долларов США [6]. ЦРУ считает реальный ВВП России в 1992 г. равным нулю. Цена нефти в долларах США за баррель (´16). Вариации в 1997-1999, 2008-2009 гг. с падением мировых цен на нефть и синхронным падением реального ВВП России. Треугольные «экономические силы» в 2006-2007 гг. толкают ВВП и цену вверх, «силы» 2008 г. их опускают. Чередование взлётов и падений закладывают основу цикличности мировой цены нефти и реального ВВП России. Источники: CIA. The World Factbook. Country Comparison; BP Statistical Review of World Energy, 2012 |
Стоит хотя бы конспективно присмотреться к «экономическим» свойствам сплайн-представления конъюнктур. При моделировании макроэкономической динамики мы насчитали 30 замечательных свойств сплайнов, полезно выделяющих их из всех аппроксимирующих функций [6]. Начнём с замечания классиков [1], говоривших о «подвижности и гибкости сплайнов». Сплайны универсальны, графические построения демонстрируют непрерывность и гладкость сплайновых моделей. Применение сплайнов при построении интерполяционных кривых на дискретных множествах точек известно как "spline-smoothing" [6] или «сплайн-сглаживание». Образно говорят, что непрерывный сплайн-ансамбль из связанных фрагментов «развешивается» на «решётчатой» функции, на множестве точек макроэкономического «графика». Сплайн-модель позволяет находить значение переменной в любой точке оси абсцисс между «узлами» «сетки» (интерполяция). Появление аналитической зависимости со всеми производными позволяет увидеть и глубже понять суть процесса и его тенденции, математически обработать его, использовав сплайны для анализа, визуализации, поиска и вычленения трендов, сезонных колебаний, циклов, для прогнозирования (экстраполяции).
|
|
|
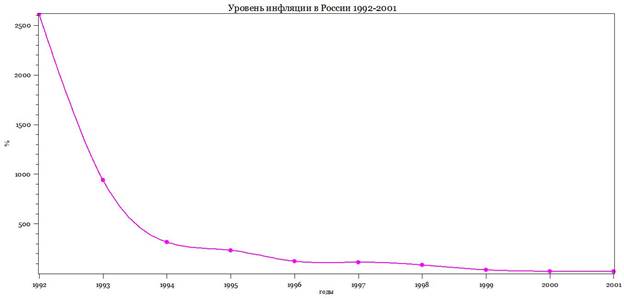
Рисунок 2 - Зависимость темпа инфляции в России от времени в 1992-2001 гг. Весь интервал наблюдений 1992-2011 гг. разбивается на две части из-за аномально высоких показателей инфляции в 1992-2001 гг., сильно отличающихся от показателей 2002-2011 гг. Размерность по оси Y - проценты. Сплайн-аппроксимация, MAGENTA. Источники: Россия. Институт стратегических исследований, CIA. The World Factbook. Country Comparison:: GDP |
Сплайны имеют инвариантную структуру, универсальную математическую форму. «Куски» сплайна аналитически самоподобны или «фракталоподобны», что позволяет экономно и однотипно их обрабатывать. Кубический сплайн эффективен, всегда существует, он единственен. Сплайн сходится быстро и равномерно на интервале [Е, F], обладая «сходимостью по норме», сплайн-построения характеризуются простотой вычислений. Аналитичность сплайна позволяет получать решения «в буквах», в этом случае привлечение аналитических возможностей систем компьютерной математики становится просто необходимым.
Важно оптимальное свойство, которым обладает кубический сплайн, первое интегральное соотношение, свойство «наилучшего приближения», «минимальности кривизны» или нормы, оно доставляется теоремой Холлидея. Кривые на графиках гладки и приятны для глаза, поскольку кубический сплайн соединяет точки «решётчатой» функции линиями с минимальной кривизной и с оптимальной (по Холлидею) «сшивкой» фрагментов в «узлах».
Отличие сплайн-подходов от классических эконометрических состоит и в том, что в «старой» эконометрике регрессионные построения теряют значение времени, при котором они получены. Сплайновые построения сохраняют время каждого отсчёта, это хронометрирует процесс, его тренд, циклы и примыкающие ветви, уточняется переход к временному планированию и прогнозированию. На фазовых портретах «новой» эконометрики (рис. 4, 5, 6) временные реперы проставляются непосредственно на кривых.
|
|
|
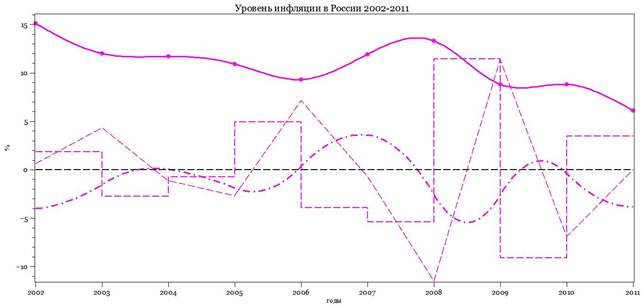
Рисунок 3 - Российская инфляция в 2002-2011 гг. Можно увидеть интересные вариации, всплеск 2007-2008 гг., до и после которого выбросы нивелируются. Размерность по оси Y - проценты. Сплайн-аппроксимация, MAGENTA. Первая производная - штрих-пунктиром, вторая (треугольная) и третья (прямоугольная) - пунктиром. Первая производная со временем уходит в нижний квадрант, определяя уменьшение инфляции в России |
Возможно построение эконометрических законов и прогнозов прямо на графических образах параметрических картин (рис 7, 8), в том числе реляционно (рис. 9). Так сплайн-технология выявляет необходимые для «новой» эконометрики закономерности. Сплайны можно символьно складывать, умножать, дифференцировать и интегрировать, аналитически находить формулы для производных, это составляет не только «достаточные» условия сплайн-анализа, но и очень удобны для перестроения моделей.
Сплайн-построения отличаются конструктивностью, решение не требует от исследователя дополнительных преобразований, допущений, размышлений. Поскольку сплайн проходит точно через все узлы «решётчатой» функции, то сплайновые построения точны институционально. Они «тонко» определяют спектральный состав экономического сигнала, улучшают интерполяцию и экстраполяцию, надёжнее накапливают и сохраняют его статистику.
Экономисты-практики требуют, чтобы экономико-математический конструкт до использования ими был исследован и применён математиками для гарантии правильности и надёжности результатов при преобразованиях. Положение это реализуется, сплайны известны со времён Л. Эйлера, а теория сплайнов, как математическая теория, - с 1949 года [10]. Как отмечал ещё Шёнберг, приближения, применяемые в страховом деле, также включают в себя понятия, тесно связывающие их со сплайнами. С тех пор сплайны широко распространились в науке, в математических исследованиях, научных и технических приложениях.
|
|
|
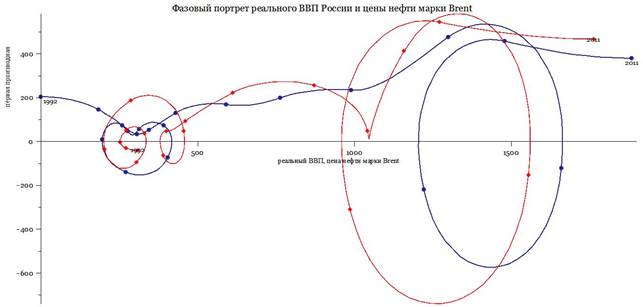
Рисунок 4 - Визуализация на фазовой плоскости циклического характера изменения двух архетипов - объёма реального ВВП России (NAVY) и мировой цены на нефть (RED) в 1992-2011 гг. По оси абсцисс - ВВП в млрд. долларов США и цена на нефть - в долларах США за баррель (´16), по оси ординат - их первые производные. Временные реперы (годы) на кривых указывают направление процесса слева (от точки 1992) направо (до точки 2011). Сплайн-аппроксимация. Идеальные циклы 1994-2002 и 2007-2010 гг. характеризуют непростую повторяемость мировой цены нефти и ведомого ею ВВП. Положительность асимптот первых производных в 2011 г. прогнозирует рост и цены нефти, и реального ВВП России |
В стохастических экономических системах при поиске и выделении циклов исследователь сталкивается с проблемой «ложной цикличности» или «эффектом Слуцкого-Юла». Было показано [7], что раз кубический сплайн обладает свойством «минимальности нормы» и он проходит между любой парой соседних точек по линии с минимальной кривизной, то не образуется паразитных «складок», типичных для аппроксимации степенными полиномами высоких порядков. В фазовом пространстве эти «складки» или «волны» между узлами превращались бы в паразитные циклы.
Использование аналитических свойств сплайна в эконофизике
В новую науку эконофизику [4] естественно входит аналитика сплайн-функций. Вместе со сплайном S(t) всегда имеются аналитически, графически и численно его три производные - dS/dt, d2S/dt2, d3S/dt3. Первая производная в экономике определяет тенденции процесса. В физике М∙dS/dt есть импульс, где М - масса, S - перемещение. Импульс «экономического действия» - количество «экономического движения» S, его величина равна произведению стоимости конкретного экономического акта М на скорость изменения обобщённой координаты dS/dt. Эта скорость характеризует способность субъекта экономики производить переоценку объективного и субъективного благосостояния. Импульс «экономического действия» - величина векторная, задающая интенсивность и направление движения экономического субъекта в экономическом пространстве [9]. Закон сохранения импульса - всеобщий принцип природы, так что экономические балансы становятся не только количественными, но и голономными, подчиняясь абсолютным законам сохранения.
|
|
|
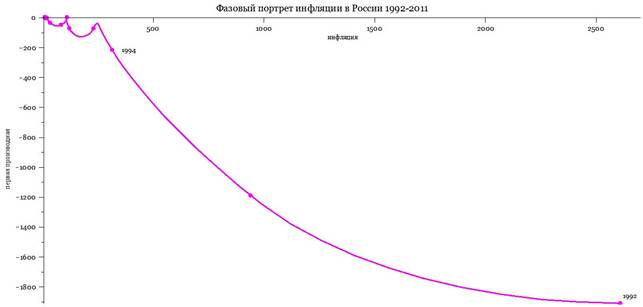
Рисунок 5 - Фазовый портрет российской инфляции в 1992-2011 гг. обнаруживает длинную гиперинфляционную ветвь 1992-1995 гг., сменяющуюся в конце появлением циклических конструкций 1996-2011 гг., которые, как и полагается во всех приличных экономиках мира, институциональны и перманентны. Сплайн-аппроксимация, MAGENTA. Первая производная в 1992-2006 гг. отрицательна, уменьшается со временем, ведя к сокращению инфляции |
Вторая производная в науке называется «ускорением», умноженная на «массу», она превращается в «силу» F = М∙d2S/dt2. Имея d2S/dt2 из уравнения сплайна и варьируя М - стоимостью экономических актов на темпоральных отрезках, получаем динамику «экономической силы». В эконофизике [4] применение второй производной как части «экономической силы» ещё ждёт своего часа. Балансы взаимодействия «экономических сил» можно также сверять по абсолютным законам сохранения. Так «экономические импульсы» и «экономические силы» управляют трансформацией экономического пространства под влиянием освоения и распределения в динамике макроэкономических потенциалов.
Кинетическая энергия описывается формулой Е = М/2∙(dS/dt)2. Закон сохранения энергии также является мировым и абсолютным, и экономика, если она наука, будет вынуждена использовать его, найдя повсеместно полезные применения. Энергию экономической активности представляют как стоимостное выражение интенсивности удовлетворения потребности в изменении объективной и субъективной оценок благосостояния посредством экономического акта. Потенциальная экономическая энергия субъекта есть стоимостное выражение его желания и возможности устранять разницу объективной и субъективной оценок благосостояния. Полную экономическую энергию субъекта образует сумма энергий экономического действия и потенциальной [9], математически её определяет гамильтониан.
Макроэкономические архетипы в фазовом пространстве
Следующим математическим конструктом при исследовании корреляционной динамики макроэкономических архетипов определим аппарат фазового анализа. Первый конструкт - сплайн-аппроксимация - хорошо проявил себя именно в нём, поскольку при построении и анализе фазовых портретов оказались необходимыми первые производные. Фазовый анализ поразительно хорошо обнаруживает и вычленяет из макроэкономических построений круговые циклические конструкции, рельефно графически их отображая [3].
|
|
|
Рисунок 6 - Фазовый портрет динамики уровня российской инфляции (проценты), более детальный анализ в период 2002-2011 гг., богатство циклических конструкций, процесс идёт справа (от точки 2002) налево (до точки 2011). Сплайн-аппроксимация, MAGENTA |
В [2] описаны математически достаточно новые для экономики понятия фазового пространства, фазового анализа динамики показателей, реализуемых в фазовом пространстве, фазовых траекторий, фазовых портретов, картин параметрических взаимозависимостей. Там фазовым портретом называлась построенная в фазовом пространстве кривая, представляющая зависимость первой производной Y'(t) некоторого непрерывного макроэкономического показателя Y(t) от самого этого показателя, время t играло роль параметра.
На фазовых портретах временные ряды макроэкономических переменных геометрически представляются семейством ориентированных гладких траекторий на фазовой плоскости ОYÝ, на координатные оси которой ставят функцию Y(t) и производную Ý(t). Значения временного параметра t при этом сохраняются и визуализируются временными реперами.
|
|
|
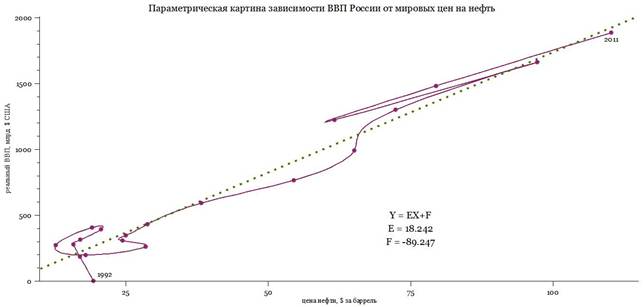
Рисунок 7 - Параметрическая картина взаимной зависимости реального ВВП России и мировых цен на нефть марки Brent в 1992-2011 гг. Сплайновая аппроксимация, MAROON. По оси ординат, млрд. долларов США - объём реального ВВП России. По оси абсцисс, долларов США за баррель - среднегодовая цена нефти. «Грубый» прямолинейный тренд RGDP = E×OILPRICE + F, рассчитываемый по методу наименьших квадратов, его коэффициенты E и F на чертеже. Образуются две редкие и интересные конфигурации, когда ВВП России растёт при снижении мировых цен на нефть (1992-1994, 2000-2001) |
|
|
|
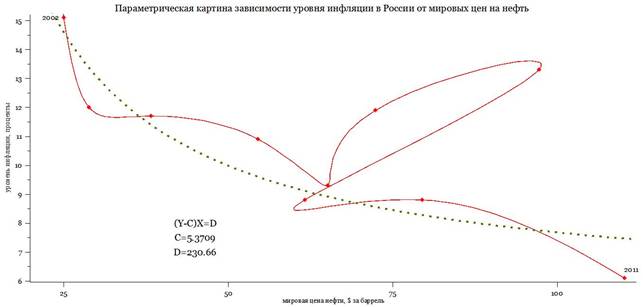
Рисунок 8 - Параметрическая картина взаимосвязи уровня инфляции в России с ценой на нефть марки Brent. Сплайн, NIAGARA LEAFGREEN. Игнорируем гиперинфляционную ветвь, строим зависимость для процесса, идущего слева от точки 2002 вправо до 2011. «Грубый» тренд найден методом наименьших квадратов, за его пределы выходит цикл 2006-2009 гг. С ростом мировой цены нефти инфляция в России гиперболически уменьшается |
Полезным приложением сплайн-анализа было получение, построение и анализ на плоскости OYZ взаимной зависимости экономических показателей или характеристик рынка в виде гладких сплайн-образов Y(t), Z(t), которые располагаются на разных осях фазового пространства (рис. 7, 8, 9). Явно сохраняется и идентифицируется реперами прямо на фазовой кривой временной параметр t. Замена временных рядов показателей фазовыми портретами или картинами их параметрических зависимостей даёт возможность улучшить восприятие и понятийное качество макроэкономических переплетений.
|
|
|
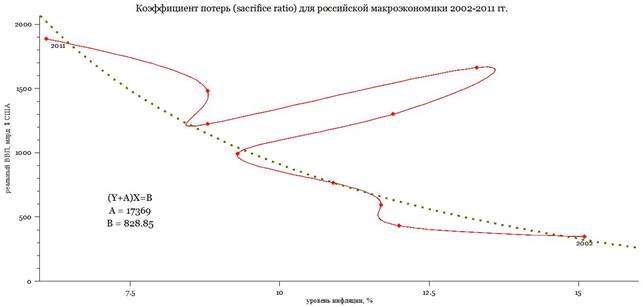
Рисунок 9 - Реляционно получаемый из рис. 7 и 8 коэффициент потерь для российской экономики 2002-2011 гг. (RED). «Грубый» гиперболический тренд (RGDP + A)×INFL = B получен методом наименьших квадратов, сплайн, NIAGARA LEAFGREEN. «Выбегающий» из тренда квазицикл 2006-2009 гг. характеризуется уходом инфляции с большими амплитудами |
Если прямолинейная зависимость реального ВВП России от мировых цен на нефть (рис. 7) достаточно хрестоматийна, то на рис. 8 покажем параметрическую картину зависимости уровня инфляции в России (ось ординат) от мировой цены на нефть (ось абсцисс) в период 1992-2011 гг. Можно определить «грубый» тренд, построив методом наименьших квадратов эконометрический гиперболический закон (INFL - C)×OILPRICE = D.
Инструментарий исследования
Третьей «составной частью» новых подходов становится повсеместное использование систем компьютерной математики для аналитического, графического и численного анализа макроэкономического поведения. Эти системы решают практически весь спектр математических задач, не требуя предварительного программирования, конструирования графиков и пр. В исследовании использована система MAPLE 16.01, к замечательным особенностям которой отнесём работу с рациональными операндами, которые исключают ошибки округления.
Заключение
Новые математические и инструментальные конструкты позволяют наметить, обнаружить, идентифицировать, вычленить из структуры макроэкономического сигнала, просчитать численно «грубые» тренды, построить графически более точные сплайновые аппроксимационные кривые, обнаружить «выбегающие» из трендов «тонкие» циклические конструкции и их ветви. Это позволяет уточнить параметрическое отношение двух важных пар архетипов в российской макроэкономике - «реальный ВВП России и мировая цена на нефть», «инфляция России и мировая цена на нефть». Из полученных двух отношений реляционно и автоматически находится третье отношение - «инфляция в России и ВВП России» - коэффициент потерь (sacrifice ratio). Эти закономерности особенно ценны для страны, экономика которой зависит от мировых цен на нефть совершенно неподобающим образом.
Рецензенты:
Винтизенко Игорь Георгиевич, доктор технических наук, профессор, ведущий научный сотрудник Научно-педагогического института ФГАОУ ВПО «Северо-Кавказский федеральный университет» Министерства образования и науки РФ, г. Ставрополь.
Тимошенко Николай Константинович, доктор экономических наук, профессор, профессор кафедры «Экономика, бухгалтерский учёт и аудит» Невинномысского технологического института (филиала) ФГАОУ ВПО «Северо-Кавказский федеральный университет» Министерства образования и науки РФ, г. Невинномысск.
Библиографическая ссылка
Боташева Ф.Б. МОДЕЛИ ВАРИАЦИИ РОССИЙСКИХ МАКРОЭКОНОМИЧЕСКИХ АРХЕТИПОВ ОТ ЦЕНЫ НЕФТИ НА МИРОВОМ РЫНКЕ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8041 (дата обращения: 09.03.2026).