Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Рудаков А.М. 1 Глаголева М.А. 1 Липанова Н.В. 1 Хмелевская Н.Д. 1 Скоробогатько Д.С. 1

---

1 Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Национальный исследовательский ядерный университет «МИФИ»

В рамках кластерной модели молекулярной ассоциации и с использованием теории идеальных ассоциированных растворов обоснованы уравнения зависимостей от концентрации термодинамических свойств (коэффициенты активности компонентов, избыточные термодинамические функции, давление пара) для бинарных смесей неэлектролитов, проявляющих положительные отклонения от закона Рауля. Основными параметрами уравнений модели является число ассоциации А1 и дисперсия распределения кластеров по стехиометрическим числам, которые рассчитываются по данным об общем давлении пара над растворами. Уравнение модели использовано для описания термодинамических свойств бинарных смесей алифатических эфиров со спиртами. Сделан вывод, что неидеальность исследованных бинарных смесей обусловлена, главным образом, молекулярной ассоциацией спиртов. Установлено, что в диметиловом эфире значения А1 и D закономерно уменьшаются с ростом молекулярной массы спирта, что согласуется с общими закономерностями ассоциации спиртов.

Статья в формате PDF

303 KB

термодинамические функции

молекулярная ассоциация

н-спирт

алифатический эфир

давление пара

1. Пригожин И., Дефей Р. Химическая термодинамика. – Новосибирск: Изд-во «Наука». Сибирское отделение, 1966.

2. Рудаков А. М. // Инженерная физика. – 2006. – № 4. – С. 40.

3. Рудаков А. М., Сергиевский В. В. // Ж. физической химии. – 2006. – Т. 80, №11. – С. 2026.

4. Alonso C. // Fluid Phase Equilibria. – 2003. – V. 212. – Р. 81-95.

5. Garriga R., Martinez S., Perez P., Gracia M. // Fluid Phase Equilibria. – 1998. – V. 147. – P. 195-206.

6. Carriga R., Sanchez F., Perez P., Gracia M. // Fluid Phase Equilibria. – 1997. – V.138. – P. 131-144.

7. Park S. J., Han K. J., Gmehling J. // J. Chem. Eng. Data. – 2007. – V. 52. – Р. 230-234.

8. Park S. J., Hana K. J., Gmehling J. // Fluid Phase Equilibria. – 2002. – V. 200. – Р. 99-109.

9. Rarey J., Horstmann S., Gmehling J. // J. Chem. Eng. Data. – 1999. – V. 44. – Р. 532-538.

10. Villamanan R. M., Martın M. C., Chamorro C. R., Segovia J. // J. Chem. Eng. Data. – 2006. – V. 51. – P. 148-152.

Введение

Добавки эфиров и спиртов к моторному топливу широко используются для повышения октанового числа. Поэтому значительное внимание в литературе уделяется изучению равновесного давления пара тройных систем спирт – эфир - алкан и соответствующих бинарных подсистем [1,4–9]. Смеси низкомолекулярных спиртов и эфиров неограниченно смешиваются друг с другом и проявляют положительные отклонения от закона Рауля. Можно полагать, что неидеальность этих смесей определяется ассоциацией спирта.

В предыдущих работах [2,3] была обоснована кластерная модель водных растворов гидрофильных неэлектролитов. В ее основу было положено предположение об образовании при взаимодействии между молекулами неэлектролита и воды кластеров, состав которых зависит от концентрации раствора. Получены уравнения, учитывающие зависимость чисел гидратации от концентрации и адекватно описывающие различные термодинамические свойства растворов. Целью настоящей работы явилось обоснование уравнений для описания термодинамических свойств бинарных смесей органических растворителей с одним ассоциированным компонентом. Проверку адекватности полученных уравнений экспериментальным данным различных авторов [6,7] проводили на примере описания свойств бинарных смесей эфиров со спиртами.

Теоретическая часть

Рассмотрим раствор двух полностью смешивающихся неэлектролитов с положительными отклонениями от закона Рауля. В ряде случаев подобное поведение смесей обусловлено молекулярной ассоциацией одного из компонентов, который определим как растворенное вещество. В общем случае ассоциация приводит к образованию химически нестойких стехиометрических кластеров растворенного вещества, содержащих различное число ассоциированных молекул (i). Соответствующий процесс отвечает реакции

, i = 1, 2,… (1)

Число молекул, присоединившееся к произвольно выбранной молекуле в кластере, определим выражением:

, (2)

где Аi – число стехиометрической ассоциации. Присутствие в растворе кластеров с различным стехиометрическим составом равносильно утверждению о существовании распределения кластеров по стехиометрическим числам ассоциации. Математическое ожидание этого распределения по определению определяется соотношением:

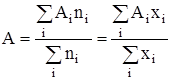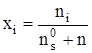, , (3)

где хi и ni – мольная доля и количество растворенного вещества, содержащего i молекул в кластере, – суммарное количество растворенного вещества, – количество чистого растворителя в одном килограмме, моль.

Можно полагать, что рассматриваемый раствор является идеальным ассоциированным [1]. В этом случае выражение термодинамической константы равновесия ki для процессов (1) имеет вид:

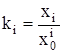. (4)

Из (3) и (4) следует, что:

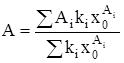, (5)

где х0 – мольная доля мономеров растворенного вещества.

После логарифмирования и дифференцирования (5) получим:

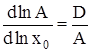, (6)

где D – дисперсия распределения кластеров по числам ассоциации. Разложение правой части (6) в ряд по степеням x0 при ограничении нулевым приближением дает:

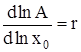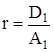, , (7)

где D1 = D(x = 1) и A1 = A(x = 1) – дисперсия и среднее распределение кластеров по числам ассоциации в стандартном состоянии при x = 1. Интегрирование (7) в интервале (, x0), где – мольная доля мономеров растворенного вещества при x = 1, приводит к

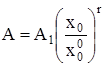. (8)

Для мольной доли растворенного вещества справедливо . Если предположить, что присоединение любой молекулы растворенного вещества к кластеру характеризуется одной и той же константой равновесия k, то путем простых преобразований получим:

и . (9)

Из (9) следует, что при x ≈ 1 . Тогда из (8) имеем:

. (10)

Пусть для приготовления раствора было взято ns моль растворителя и такое количество N, моль, мономерных молекул растворенного вещества, что после наступления равновесия в растворе оказалось n моль различных кластеров растворенного неэлектролита. Очевидно, что N = n(1+A). В этом случае для коэффициента активности растворителя fs будет справедливо:

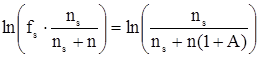. (11)

После простых преобразований имеем:

, (12)

или, учитывая (10) и малую по сравнению с 1 величину Ах, находим:

. (13)

Принимая во внимание связь между коэффициентами активности уравнением Гиббса –Дюгема, после простых преобразований для коэффициента активности растворенного вещества f находим:

. (14)

В свою очередь определение избыточной мольной энергии Гиббса и соотношения (13) и (14) позволяют записать:

(15)

Подставляя (15) в уравнение Гиббса – Гельмгольца, для избыточной мольной энтальпии находим:

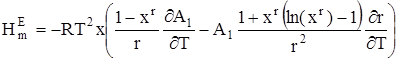. (16)

В случае, когда D1 зависит от Т, с использованием определения дисперсии дискретного распределения получим:

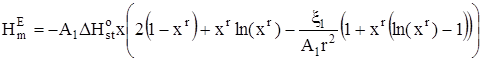, (17)

где – изменение стандартной мольной энтальпии при присоединении молекулы неэлектролита к кластеру, – величина третьего центрального момента распределения кластеров по стехиометрическим числам ассоциации в стандартном состоянии.

Для избыточного мольного объема в соответствии с его определением получено следующее выражение:

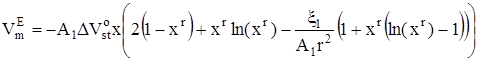, (18)

– изменение стандартного мольного объема, сопровождающее присоединение молекулы неэлектролита к кластеру. В предположении об идеальности паровой фазы с использованием (13) и (14) можно записать следующее выражение для давления пара над раствором:

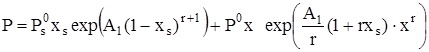, (19)

где и – давление насыщенного пара над чистыми – растворителем и растворенным веществом, соответственно. Полученные уравнения использованы для описания литературных экспериментальных данных [6,7,10] по общему давлению пара и избыточным свойствам бинарных смесей спирт – эфир. При описании этих данных минимизацию проводили с использованием стандартных отклонений σ:

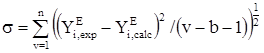, (20)

где YE – избыточное термодинамическое свойство или давление пара, v – количество экспериментальных точек, b – число эмпирических параметров в уравнении.

Результаты и обсуждение

Описание концентрационных зависимостей различных свойств проведено при выборе в качестве растворителя любого из компонентов смесей. Установлено, что минимальные значения σ во всех случаях меньше при выборе в качестве растворителя эфира. Это предполагает, что неидеальность исследованных бинарных смесей обусловлена, главным образом, молекулярной ассоциацией спиртов.

Давление пара. Основным параметром уравнений модели является число ассоциации А1, которое рассчитывается по данным об общем давлении пара над растворами. Результаты, представленные в табл. 1, свидетельствуют, что уравнение (19) адекватно описывает экспериментальные данные. В диметиловом эфире значения А1 и D1 закономерно уменьшаются с ростом молекулярной массы спирта, что согласуется с общими закономерностями ассоциации спиртов.

Таблица 1

Описание экспериментальных данных по равновесию жидкость – пар

уравнением (19) (растворитель эфир)

Избыточные энтальпия и энтропия. В литературе имеются сведения об энтальпиях смешения при различных составах рассматриваемых систем [7,10]. Результаты, представлены в табл. 2.

Таблица 2

Описание экспериментальных данных по энтальпии уравнением (17) (растворитель эфир)

Наличие данных по GE и HE позволяет провести расчет ТSE по определению ТSE = HE - GE в двух вариантах. В первом варианте ТSE рассчитывали с использованием значений GE и HE, вычисленных по уравнениям (15) и (17). Эти результаты на рис. 1 и 2 представлены сплошными линиями. Во втором варианте использовали экспериментальные данные по HE, а значения GE рассчитывали по уравнению (15). Результаты на рис. 1,2 представлены точками.

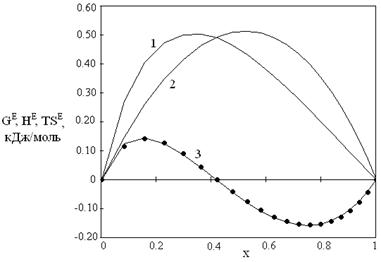
Рис. 1. Зависимости от мольной доли спирта избыточных термодинамических функций для системы диметиловый эфир – метанол при 323.15 К: 1 – HE, 2 - GE, 3 – TSЕ

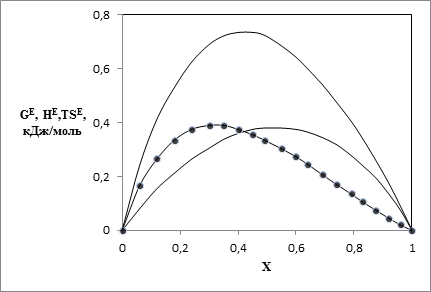
Рис. 2. Зависимости от мольной доли спирта избыточных термодинамических функций для системы диметиловый эфир – этанол при 323.15 К: 1 – HE, 2 - GE, 3 – TSЕ

Результаты различных оценок ТSE практически совпадают. При этом уравнения модели хорошо описывают как обычные, так и знакопеременные зависимости значений ТSE от состава. Рост молекулярной массы спиртов приводит к уменьшению энергий Гиббса, их смесей с диметиловым эфиром.

Таким образом, уравнения кластерной модели адекватно описывают экспериментальные данные по давлению пара и энтальпии смешения. По данным табл. 1 можно отметить, что параметр ассоциации спирта в стандартном состоянии А1 убывает от наибольшего значения для системы диметиловый эфир – метанол до минимального значения для системы диметиловый эфир – бутанол, то есть с ростом длины алифатического радикала спирта.

Из данных табл. 2 по значениям (энергия, высвобождающаяся при распаде 1 моля ассоциатов спиртов), учитывая значение RT, можно сделать вывод об энергетике ассоциатов. Величина для большинства систем находится в пределах от 1.7 до 10.6 кДж/моль (табл. 2). Принято считать, что энергия водородной связи находится в пределах от 5 до 30 кДж/моль. Следовательно, ассоциаты спиртов в рассмотренных эфирах образуются за счет водородных связей и ван-дер-ваальсовских взаимодействий.

Рецензенты:

Соловьев Сергей Николаевич, д.х.н., профессор, зав. каф. общей и неорганической химии Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Российский химико-технологический университет им. Д. И. Менделеева», г. Москва.

Аллахвердов Грант Рантович, д.х.н., профессор, Институт фармацевтических реактивов РЕФАРМ, г. Москва.

Библиографическая ссылка