Анализ потребностей современной практики в области экономики малого и среднего предпринимательства, изучение теоретических положений и разработок формирования и принятия управленческих решений показал, что ранее используемые традиционные схемы не могут в современных условиях служить основой для дальнейшего развития предприятий малого и среднего предпринимательства.
Для реализации инновационного направления развития нужна принципиально новая методология научно-прикладных исследований и прогнозирования на основе математического моделирования и вычислительного эксперимента с помощью компьютерных информационных систем поддержки принятия управленческих решений синтеза современных численных методов и компьютера.
Математическое моделирование обладает широкими возможностями, а метод математического моделирования более универсален, поскольку [3, с. 76]: во-первых, позволяет с помощью одного настроенного устройства (имеется в виду компьютер с развитой периферией и специализированным программным комплексом) осуществить решение целого класса задач, имеющих одинаковое математическое описание; во-вторых, обеспечивает простоту перехода от одной задачи к другой за счет изменения значений параметров исследуемой системы, различных возмущений и начальных условий; в-третьих, реализует возможность моделировать (отрабатывать) систему по частям, благодаря декомпозиции; в-четвертых, использует непрерывно совершенствующуюся вычислительную технику.
Основным преимуществом математического моделирования по сравнению с аналитическим является возможность решения задач исключительной сложности.
Кроме того, математическое моделирование позволяет обобщать результаты на основе параметрических исследований, прогнозировать возможное поведение при изменении определяющих показателей, определять скрытые резервы структуры управления предприятием и «узкие» места в ней, уменьшать степень финансового риска, что при ограниченных ресурсах, и, особенно, в рамках ограничения во времени приобретает первостепенное значение.
Построение качественных математических моделей является основой реализации системного анализа, занимая центральное место в организации исследований и проектирования любой экономической системы, ее подсистемы управления.
Для осуществления сказанного необходимо преодолеть разобщенность наук и еще на этапе общего описания объекта малого и среднего предпринимательства объединить отдельные частные исследования в единое целое. Такое объединение возможно благодаря современным компьютерным информационным системам поддержки принятия управленческих решений. Оно осуществляется с помощью целой иерархии математических моделей отдельных предприятий, входящих в состав малого и среднего предпринимательства.
Цикл вычислительного эксперимента «предприятие малого и среднего предпринимательства – математическая модель – алгоритм – пакет прикладных программ – компьютер» отражает основные этапы процесса познания в нынешнем компьютерном воплощении.
Экспериментирование с математической моделью, а не с объектом сопровождается оперативным накоплением информации об объекте, вскрывающей его внутренние многофункциональные связи и позволяющей судить о его интегральных свойствах. Данный алгоритм ведет к значительной экономии материальных и трудовых затрат по сравнению с традиционным экспериментальным подходом. Существуют два вида математических описаний процесса – детерминированное и статистическое.
Детерминированное описание строится на основе фундаментальных теоретических законов и закономерностей экономики. Множество практических задач, анализ процессов которых осуществляется с учетом действия случайных факторов, источниками которых служат воздействие внешней среды, ошибки, шумы и отклонения различных показателей, возникающие внутри системы. В отличие от других методов, математическое моделирование оказывается весьма приспособленным для изучения процессов с учетом случайных факторов.
Трудность статистического описания при исследовании процессов методом математического моделирования состоит в выборе вектора состояния системы, элементы которого реально характеризовали бы реализуемый процесс.
Следует указать на то, что компоненты вектора состояния системы необходимо определять как средние значения по данным большого числа реализаций процесса. Оценки искомых показателей приобретают статистическую устойчивость при наличии большого числа реализаций и могут быть приняты с достаточной для практики точностью в качестве приближенных значений искомых компонент вектора состояния системы.
Необходимо отметить, что между традиционными методами (аналитическим и натурным экспериментом) и новой научно-прикладной методологией нет никакого противоречия.
В этих условиях математическое моделирование выступает как объединяющий и цементирующий фактор, благодаря которому классические методы получают новое измерение и дополнительное обоснование, фундаментальные исследования – четкую направленность, а прикладные разработки – теоретическую базу.
Современной особенностью математического моделирования, на наш взгляд, является быстрое и постоянное совершенствование компьютерных информационных систем, которое в значительной степени стимулирует развитие численных методов исследования в разных областях экономики, в том числе в подсистемах поддержки принятия управленческих решений.
Существующие в настоящее время пообъектные подходы к формированию экономико-математических моделей и их решению (когда практически под каждый объект малого и среднего предпринимательства создается своя модель) представляются нерациональными поскольку связаны с необходимостью выполнения каждый раз неоправданно большого объема подготовительной работы, дублирования, не обеспечивают накопления и обобщения опыта создания и применения моделей с единых методологических позиций.
Этот недостаток можно устранить путем разработки универсальных моделей, ориентированных на решение широкого круга экономических задач, стандартизацией структурных блоков модели и применением унифицированных приемов моделирования.
С учетом накопленного опыта создание моделей должно осуществляться с соблюдением следующих принципов [3, с. 85].
Первый принцип – модульный принцип организации структуры экономико-математической модели. Модульный принцип обеспечивает независимость формирования результирующей модели экономического объекта любого уровня от конкретных методов расчета и, как следствие, возможность сравнительно простого перехода к более совершенным методам расчета характеристик составных частей задачи путем замены одного модуля другим.
Второй принцип – унификация моделей. В настоящее время математическое моделирование имеет уровень развития и совершенствования, когда возможен переход от поштучного производства к созданию унифицированных моделей, позволяющих с единых позиций рассматривать достаточно широкий круг задач. Такими свойствами обладает, например, имитационная модель работы предприятия малого и среднего предпринимательства.
Все прикладные модели рассматриваются как частный случай унифицированной модели, а условия перехода к той или иной модели оговариваются заданием исходных данных.
Использование указанного принципа позволяет значительно быстрее определить эффективные методы решения комплексных задач, исключить ошибки при переходе к решению новых задач и значительно упростить процедуру освоения математических моделей пользователем. Использование модульного принципа позволяет расширить материальную базу унификации модели и прежде всего в области нелинейной оптимизации.
Третий принцип – сочетаемость с другими моделями. Реализация данного принципа требует в общем случае разработки специальных методов исследований. Принцип сочетаемости так же, как и принцип унификации, направлен, в первую очередь, на обеспечение оперативности формирования модели предприятия малого и среднего предпринимательства в целом и простоты ее освоения.
Четвертый принцип – выделение базовых моделей. Согласно этому принципу процесс создания модели предприятия разбивается на ряд этапов:
– отбор или формирование заново модели окружающей среды, элементов и подсистем, входящих в состав объекта; – построение базовой модели; – модификация базовой модели оптимизации или ее усложнение под конкретные задачи. Два первых этапа наиболее трудоемкие и осуществляются совместно специалистами по численным методам и экономистами. Третий этап существенно проще первых двух, легко поддается формализации и может выполняться исследователями, не являющимися, например, специалистами в области принятия управленческих решений.
В итоге принцип выделения базовой модели обеспечивает сравнительную простоту и доступность в ее использовании для проведения широкого круга прикладных исследований. При этом реальной становится возможность одновременного создания предприятия малого и среднего предпринимательства и его математической модели – «математического дублера», который в дальнейшем может быть использован при исследовании и при повседневной управленческой деятельности.
Использование методов математического моделирования и принятие на их основе обоснованных решений по управлению деятельностью предприятия можно считать важным конкурентным преимуществом предприятий малого и среднего бизнеса, поскольку разработка и внедрение новой системы управленческих технологий позволяет повысить эффективность функционирования предпринимательских структур и обеспечить реализацию стоимостно-ориентированного подхода в управлении бизнесом.
Ввиду того, что предприятие само по себе является сложной социально- экономической системой, функционирующей в условиях неопределенности, получение комплексной оценки финансового обеспечения предприятия является сложной задачей не только с экономической, но и с математической точки зрения. Как следствие, возрастает актуальность разработки экономико-математических моделей, которые могут позволить осуществлять комплексную оценку финансового состояния предприятия с достаточной точностью и надежностью.
В сочетании использования экономико-математических моделей и современных компьютерных технологий, результаты анализа состояния экономических объектов и процессов, экономическое прогнозирование развития экономических процессов, выработка управленческих решений на всех уровнях хозяйственной иерархии, получение точных результатов диагностики и оценки финансового состояния не только сокращают время оперативного принятия решений, но и способствуют повышению конкурентоспособности малого и среднего предпринимательства.
Совместное применение экономико-математических методов и моделей и методов экономического анализа позволяет получить качественно новые выводы об экономических процессах и явлениях, перспективах их развития. Экономико-математическое моделирование в настоящее время становится все более востребованным в процессе проведения экономических исследований и используется в качестве одного из основных инструментов количественного анализа статистических данных о деятельности предприятия. Это объясняется тем, что, во-первых, математическое моделирование можно рассматривать как эффективное средство структурированного, более компактного и обозримого представления исходной информации. Во-вторых, существует целый ряд типичных управленческих ситуаций, которые допускают формализацию, где именно математические подходы и соображения обоснованно становятся решающими.
Выше обозначенные проблемы рассматриваются в статье на основе конкретной практической деятельности предприятия малого бизнеса – торгового предприятия (ТП). На реализацию торгового процесса оказывает влияние большое количество факторов, но характерными из них являются: конкуренция, сезонность, состояние законодательной базы, покупательская способность граждан, средняя заработная плата, уровень техники и технологий и т.д. Все это усиливает необходимость многофакторного анализа результатов деятельности и разработки мероприятий по повышению эффективности малого ТП.
С этой целью представляется целесообразным выделить основные этапы математического моделирования, на каждом из которых в соответствии с методологией многофакторного статистического анализа используется соответствующий метод (рис. 1) [5, с. 35]:
этап 1 – выделение главных факторов, оказывающих влияние на весь процесс реализации продукции предприятием;
этап 2 – оценка корреляционной связи главных факторов и выручки ТП;
этап 3 – прогноз выручки ТП на заданный период на основе качественной модели регрессии.
Реализация данной модели выполнялась с применением теории многомерных методов статистики и стандартного пакета прикладных статистических программ: ОЛИМП «СтатЭксперт» [4].

Рисунок 1. Блок-схема экономико-математической модели
Для проведения исследования сформирована таблица исходных данных (табл. 1 – фрагмент). Показателем в данном исследовании является выручка предприятия Y. В качестве факторов Xj определены следующие виды реализуемой продукции: X1 – молочная; X2 – мясная; X3 – консервированная; X4 – крупы, макароны; X5 – масложировая; X6 – рыбная; X7 – полуфабрикаты; X8 – кондитерская; X9 – ликероводочная; X10 – пивная; X11 – соки, воды; X12 – хлебобулочная.
В качестве периода исследования выбран временной интервал с 2009 по 2011 годы, помесячно. Значения всех признаков измеряются в тысячах рублей.
Таблица 1. Динамика показателей деятельности торгового предприятия
|
|
Y |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
x11 |
x12 |
|
2009год |
|||||||||||||
|
1 |
655 |
43.4 |
55.9 |
49.8 |
31 |
80.7 |
18.6 |
31 |
62.1 |
99.3 |
93.1 |
55.8 |
35 |
|
2 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
12 |
653 |
49.2 |
63.2 |
51.7 |
36.2 |
78.2 |
31.1 |
33.6 |
66.2 |
96.5 |
92.9 |
23.9 |
30.7 |
|
2010год |
|||||||||||||
|
13 |
650 |
49.7 |
61.2 |
50.1 |
37.1 |
77.7 |
30.9 |
33.1 |
65.3 |
97.5 |
95.3 |
22.1 |
30.5 |
|
14 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
24 |
515 |
36.9 |
47.2 |
36.5 |
25.4 |
62.5 |
25 |
23 |
51.7 |
77.5 |
81.4 |
20.9 |
27.7 |
|
2011год |
|||||||||||||
|
25 |
502 |
37.5 |
45.1 |
34.3 |
24.3 |
60.1 |
24.9 |
21 |
50.5 |
76.4 |
83.1 |
18.8 |
26.2 |
|
26 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
36 |
417 |
35.2 |
36.1 |
18.2 |
17.1 |
45.7 |
18.1 |
32.5 |
47.1 |
49.2 |
79.4 |
17.7 |
20.9 |
Этап 1. Значения показателей реализации продукции Хj торгового предприятия являются лишь его косвенными характеристиками. На самом же деле существуют скрытые, не наблюдаемые непосредственно признаки (факторы), число которых мало и которые определяют значения наблюдаемых показателей реализации продукции. Эти внутренние признаки в факторном анализе принято называть главными факторами, а сам метод «факторный анализ» – методом формирования гипотез [1, с. 63].
Результаты вычислений с помощью модуля «Факторный анализ» программного пакета представлены в таблице 2 и таблице 3. Кроме того, в табл. 2 представлены значения общности [1, с. 63].
Таблица 2. Матрица повернутых факторных нагрузок и общности
|
|
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор 4 |
Общность |
|
x1 |
0.868 |
0.078 |
0.153 |
0.340 |
0.898 |
|
x2 |
0.853 |
0.100 |
0.179 |
0.426 |
0.950 |
|
x3 |
0.862 |
0.310 |
0.317 |
0.174 |
0.970 |
|
x4 |
0.805 |
0.254 |
0.196 |
0.421 |
0.929 |
|
x5 |
- 0.863 |
0.117 |
0.308 |
0.316 |
0.954 |
|
x6 |
- 0.882 |
0.300 |
0.161 |
0.195 |
0.931 |
|
x7 |
0.507 |
0.021 |
0.172 |
0.833 |
0.981 |
|
x8 |
- 0.831 |
0.193 |
0.342 |
0.354 |
0.970 |
|
x9 |
- 0.913 |
0.034 |
0.278 |
0.186 |
0.947 |
|
x10 |
0.149 |
-0.932 |
0.264 |
0.023 |
0.961 |
|
x11 |
0.244 |
-0.314 |
0.879 |
0.154 |
0.954 |
|
x12 |
- 0.816 |
0.210 |
0.432 |
0.203 |
0.938 |
Таким образом, в соответствии с данными таблицы 2 на процесс торговли оказывают воздействие четыре главных фактора. В табл. 3 представлены данные, отражающие динамику воздействия главных факторов на процесс торговли. Для удобства представления данных табл. 3 по тексту она трансформирована.
Таблица 3. Динамика влияния главных факторов на процесс торговли
|
Месяц |
F1 |
F2 |
F3 |
F4 |
|
2009 год |
||||
|
1 |
-0.206 |
-0.532 |
4.616 |
0.065 |
|
2 |
… |
… |
… |
… |
|
12 |
1.131 |
0.632 |
-0.398 |
0.92 |
|
2010 год |
||||
|
13 |
1.123 |
0.86 |
-0.609 |
0.865 |
|
14 |
… |
… |
… |
… |
|
24 |
0.209 |
-0.262 |
0.055 |
-0.805 |
|
2011 год |
||||
|
25 |
0.198 |
-0.082 |
-0.242 |
-1.091 |
|
26 |
… |
… |
… |
… |
|
36 |
-2.164 |
-0.27 |
-0.24 |
2.464 |
Идентификация главных факторов по значениям факторных нагрузок (табл. 2) и динамике их воздействия на процесс торговли (табл. 3) показывает, что объективно существует четыре главных фактора, которые оказывают влияние на реализацию товаров данного ТП: – конкуренция; – сезонность; – контингент покупателей; – доходы покупателей.
Этап 2. В матрицу значений главных факторов (табл. 3) добавляется столбец значений показателя Y (выручка) из табл. 1 и, таким образом, сформирована таблица для дальнейшего проведения исследования [1, с. 72].
Используя корреляционный анализ, решалась задача выявления степени и характера влияния главных факторов Fj на показатель Yи их взаимного влияния [1, с. 36]. Значения парных коэффициентов корреляции вычислялись с применением программы «СтатЭксперт», которая работала в режиме «Корреляция» [4] (табл. 4.).
Таблица 4. Матрица парных корреляций выручки и главных факторов
|
|
Y |
F1 |
F2 |
F3 |
F4 |
|
Y |
1.000 |
- 0.837 |
- 0.302 |
0.333 |
0.314 |
|
F1 |
- 0.837 |
1.000 |
-0.008 |
-0.011 |
-0.021 |
|
F2 |
- 0.302 |
-0.008 |
1.000 |
-0.025 |
0.010 |
|
F3 |
0.333 |
-0.011 |
-0.025 |
1.000 |
-0.008 |
|
F4 |
0.314 |
-0.021 |
0.010 |
-0.008 |
1.000 |
|
Критическое значение на уровне 80% при 2 степенях свободы = +0.1446 |
|||||
Фактор F1(конкуренция) на изменение выручки оказывает высокое отрицательное влияние (r21 = -0,837), фактор F2(сезонность) – умеренное отрицательное влияние (r31 = -0,302). Влияние фактора F3 (контингент покупателей) и фактора F4 (доходы покупателей) на изменение выручки оказывают умеренное положительное влияние (r41 = 0,333; r51 = 0,314, соответственно). Взаимная корреляция между факторами отсутствует, что, во-первых, подтверждает теоретические положения о независимости главных факторов, во-вторых, данный факт свидетельствует о хорошем качестве регрессионной модели в будущем.
Таким образом, для построения модели регрессии выручки воспользуемся данными всех главных факторов.
Этап 3. На третьем этапе исследования программа «СтатЭксперт» работала в режиме «Линейная множественная регрессия» [4]. В результате расчётов регрессионная модель изменения выручки от главных факторов имеет вид (табл. 5):
Y = 528,549 – 79,955F1 – 24,538F2 + 32,487F3 + 30,866F4, (1)
где Y– выручка торгового предприятия; F1 – конкуренция; F2 – сезонность; F3 – контингент покупателей; F4 – доходы покупателей.
Параметры модели bi значимы, так как расчётные значения их коэффициентов Стьюдента tрасч, представленные в табл. 5, больше табличного (критического) значения (табл. 5): |tрасч|>tкр= 1,055.
Включенные в модель факторы на 96,63 % описывают изменение выручки (табл. 6). Множественный коэффициент детерминации ![]() значим, так как расчётное значение критерия Фишера Fрасч больше табличного (табл. 6): Fрасч = 4587,125 >Fтабл(α = 0,05; k1 = 4; k2 = 31) = 2,69.
значим, так как расчётное значение критерия Фишера Fрасч больше табличного (табл. 6): Fрасч = 4587,125 >Fтабл(α = 0,05; k1 = 4; k2 = 31) = 2,69.
Таблица 5. Оценка параметров модели выручки торгового предприятия
|
|
Коэффициент |
Среднекв. отклонение |
t-значение |
Эластичность |
Бета-коэф-фициент |
Дельта коэф-т |
|
Св. член |
528.549 |
0.461 |
1147.554 |
0.000 |
0.000 |
0.000 |
|
F1 |
-79.955 |
0.455 |
-175.580 |
-0.036 |
0.512 |
0.697 |
|
F2 |
-24.538 |
0.449 |
-54.603 |
-0.002 |
0.146 |
0.199 |
|
F3 |
32.487 |
0.447 |
72.748 |
0.002 |
0.051 |
0.070 |
|
F4 |
30.866 |
0.449 |
68.679 |
0.019 |
0.025 |
0.033 |
|
Критическое значение t-распределения пpи 31 степени свободы (Рд=95 %) = +1,055 |
||||||
Оценка влияния отдельных факторов, включенных в модель, на изменение выручки по эластичности, позволяет сделать вывод о том, что отклонение любого из главных факторов на 1 % практически не приводит к отклонению выручки от ее среднего (табл. 5).
Оценка влияния вариации отдельных факторов, включенных в модель, на изменение выручки побета-коэффициента, позволяет сделать вывод о том, что наибольшее влияние оказывает конкуренция (b1 = 0,512, табл. 5) [1, с. 123]. Конкуренция как главный фактор многогранна по своей сути и поэтому ее изменчивость существенно влияет на колебания значений выручки. Кроме того, вариация факторов оказывает влияние на вариацию значений выручки, то есть она чувствительна к колебаниям значений главных факторов. Это объясняется рядом причин: конкуренция оказывает непосредственное влияние на выручку; сезонные колебания вызывают спады и подъемы выручки в зависимости от спроса на определенные группы товаров; на размер выручки оказывает влияние скорость товарооборота, которая, в свою очередь, зависит от контингента покупателей и их доходов.
Доля вклада каждого фактора Fj в суммарное влияние всех факторов, включенных в модель, оценивается дельта-коэффициентом, и как видно из табл. 5 вклад фактора F1 в суммарное влияние факторов, включенных в модель, составляет 69,7 % (D1 = 0,697) и является наибольшим. Это вполне объяснимо – конкуренция для торговли самый главный фактор из всех рассматриваемых и под ее влиянием происходят существенные изменения товарооборота за счет потери (приобретения) покупателей.
Таким образом, при прогнозировании и планировании работы ТП необходимо учитывать распределение степени влияния главных факторов на изменение выручки.
Таблица 6. Характеристики остатков выручки
|
Характеристика |
Значение |
|
Среднее значение |
0,000 |
|
Дисперсия |
6,576 |
|
Приведенная дисперсия |
7,637 |
|
Средний модуль остатков |
1,919 |
|
Относительная ошибка |
0,358 |
|
Критерий Дарбина-Уотсона |
1,977 |
|
Коэффициент детерминации |
0,9663 |
|
F-значение (n1 = 4, n2 = 31) |
4587,125 |
|
Критерий адекватности |
98,490 |
|
Критерий точности |
96,941 |
|
Критерий качества |
97,329 |
|
Уравнение значимо с вероятностью 0,95 |
|
Прогнозирование выполняется с использованием исключительно качественной модели. Модель считается качественной, если она адекватна и имеет высокий уровень точности. Надо отметить, что проблема создания адекватной математической модели реального процесса, а в данном случае, модели изменения выручки торгового предприятия – исключительно трудоемкая задача. В конечном счете, окончательный успех построения модели фактически полностью зависит от степени разрешимости этой узловой проблемы.
Оценка качества модели выполняется по характеристикам остаточной компоненты, значения которой рассчитываются по формуле [2, с. 59]:
ei = yi- ![]() , (2),
, (2),
где εi – i-тое значение остаточной компоненты выручки; уi – i-тое фактическое значение выручки; ![]() – i-тое значение выручки, полученное с помощью модели (1).
– i-тое значение выручки, полученное с помощью модели (1).
Модель (1) является адекватной (98,49 %), так как свойства её остаточной компоненты выполняются (табл. 6).
Математическое ожидание остаточной компоненты e равно нулю.
Уровни остаточной компоненты не коррелированы между собой, так как расчётное значение критерия Дарбина – Уотсона больше верхней границы dв табличного (dн= 1,24; dв= 1,73): dрасч= 1,977 >dв = 1,73.
Уровни остаточной компоненты e распределены по нормальному закону, так как расчетное значение RS-критерия:
![]()
попадает в интервал табличных значений (RSверх= 3,58; RSнижн = 5,04).Значение дисперсии остатков получено из табл. 5, а максимальное и минимальное значение остатков из табл. 6.
Уровни остатков являются случайными, так как фактическое количество поворотных точек («пиков») Рфакт= 27 (табл. 7) больше расчетного:
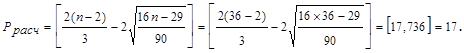
Таблица 7. Значения остатков выручки
|
|
Y |
Ŷ |
eабс |
eотн |
«пики» |
|
1 |
655.7 |
650.9 |
4.711 |
0.718 |
0 |
|
2 |
… |
… |
… |
… |
… |
|
35 |
368.2 |
368.2 |
-0.053 |
-0.015 |
1 |
|
36 |
417.2 |
417.1 |
0.039 |
0.009 |
0 |
Модель имеет достаточно высокий уровень точности – 96,941 % (табл. 6), при значении средней относительной ошибки eотн = 0,358 % (табл. 6). Интегральный критерий качества модели составляет 97,329 % (табл. 6). Следовательно, модель значима с вероятностью 0,95 и может применяться для прогноза выручки ТП.
На завершающем этапе исследования с помощью модели (1) выполнен прогноз выручки. Результаты расчёта прогнозных значений представлены в табл. 8 и на рис. 2.
Таблица 8. Точечный и интервальный прогноз выручки
|
Упреждение |
Прогноз |
Нижняя граница |
Верхняя граница |
|
январь |
392,264 |
388,933 |
395,595 |
|
февраль |
412,303 |
407,685 |
416,921 |
|
март |
376,155 |
371,526 |
380,784 |
Надёжность прогноза имеет достаточно высокий уровень – 95 %. В январе 2012 года предполагается уменьшение выручки по сравнению с декабрем 2011 года на 5,98 %. В феврале 2012 года предполагается рост выручки магазина по сравнению с январем на 5,1 %. В марте 2012 года предполагается уменьшение выручки по сравнению с февралем на 9,6 %.
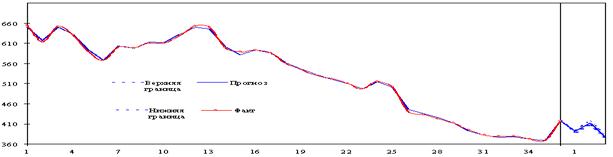
Рисунок 2. Аппроксимация и прогноз выручки ТП
Анализ рис. 2 показывает, что в 2009 году выручка практически находилась на одном уровне, а за весь последующий период наблюдается тенденция ее уменьшения, что является следствием ряда причин: ужесточение конкуренции, снижение доходов населения под влиянием инфляции и кризиса и, как следствие, снижение спроса, снижение выручки.
На основании полученного прогноза выручки на первый квартал 2012 года группа независимых экспертов предложила провести ряд мероприятий, способствующих ее увеличению. Это снижение цен, расширение и обновление ассортимента, усиление рекламной деятельности. Расчеты и анализ предлагаемых экспертами мероприятий показали, что спрос увеличится на 11,47 тыс. руб. Увеличение товарооборота предполагается на 4200 руб., а ускорение оборачиваемости товаров приведет к увеличению выручки на 4050 руб. Все это свидетельствует о правильно выбранной тактике в конкурентной борьбе.
Таким образом, грамотный подход в совместном использовании экономико-математической модели и финансово-экономического анализа позволили выявить ряд агрегированных факторов, оказывающих существенное влияние на процесс реализации продукции. В свою очередь, это дало возможность принять ряд грамотных управленческих решений, способствующих увеличению выручки малого торгового предприятия и, в конечном счете, выжить ему в конкурентной борьбе на данном этапе.
Рецензенты:
Бухтиярова Татьяна Ивановна, д.э.н., профессор, профессор кафедры «Учета и анализа хозяйственной деятельности» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Финансовый университет при Правительстве России», г. Челябинск.
Переверзев Павел Петрович, д.т.н., профессор кафедры «Информационные системы и технологии» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Российский государственный торгово-экономический университет» Челябинский институт (филиал), г. Челябинск.
Библиографическая ссылка
Якушев А.А. ПРИНЯТИЕ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ НА ОСНОВЕ СИСТЕМНОГО ПОДХОДА И МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ // Современные проблемы науки и образования. 2012. № 6. ;URL: https://science-education.ru/ru/article/view?id=7936 (дата обращения: 01.01.2026).



