В диагностике технических систем, подвергшихся некорректному внешнему воздействию, нередко проявляются дефекты, при которых связь между признаками и причинами неисправностей носит неоднозначный характер. Простые двузначные утверждения типа «испраный-1» – «неисправный-0» недостаточны, поскольку современные диагностические системы должны распознавать опасные условия функционирования, причины и тип возникшей неисправности, которые не поддаются четкому и однозначному описанию.
В работах [5],[6] говорится, что важным шагом в любом методе диагностики отказов является построение адекватной математической модели. Диагностирование неисправностей системы при помощи детерминистических методов распознавания дефектов эффективно только при наличии математической модели ее функционирования или процесса. Эти модели в большинстве случаев решаемы с использованием численных методов, что накладывает ограничение на их использование в реальном времени при поиске неисправностей и управлении технической системой. Почти все реальные процессы функционирования технических систем имеют нелинейное поведение, и для них характерно возникновение нештатных ситуаций. Эти ситуации сопряжены с нечеткостью поступающей диагностической информации. В этих случаях используют экспертов, то есть происходит вмешательство человека в процесс диагностирования и управления технической системой. Исключение человека из процесса управления или поиска дефектов в таких условиях возможно с использованием методов нечеткой логики позволяющих обрабатывать знания и делать заключения на основе рассеянных, неточных, разбросанных и неполных знаний. В работе представляются предпосылки построения таких диагностических систем, предлагается метод их многокритериального проектирования.
Аппарат нечетких множеств применяется для решения задач, в которых исходные данные являются ненадежными и слабо формализованными. Толчком к развитию новой метаматематической теории явилась опубликованная в 1965 г. работа L.Zadeh «Fuzzy Sets», в которой он расширил классическое понятие множества, допустив, что характеристическая функций (функция принадлежности элемента множеству) может принимать любые значения в интервале (0,1), а не только 0 или 1. Такие множества были названы им нечеткими (fuzzy). В 1993 г B.Kosko доказал теорему «Fuzzy Approximation Theorem», согласно которой любая математическая система может быть аппроксимирована системой основанной на нечеткой логике. Согласно [1], сильными сторонами применения математического подхода основанного на нечетких множествах и нечетких логиках являются: описание условий и метода решения задачи на языке, близком к естественному; универсальность и эффективность. Но имеются характерные недостатки: исходный набор постулируемых нечетких правил формируется экспертом и может оказаться неполным или противоречивым; вид и параметры функции принадлежности, описывающих входные и выходные переменные системы, выбираются субъективно и могут оказаться недостаточно адекватно отражающими реальную действительность.
Функция принадлежности и нечеткие множества, согласно [1] определяются при условии, что задано универсальное множество Е с элементами 
, а также некоторое свойство S, определяющее принадлежность элементов к множеству, тогда:
Определение 1. Если подмножество 
и определяется как множество упорядоченных пар 
, а его элементы , удовлетворяющие свойству S, принимают значения 
и 
, то множество А является четким.
Определение 2. Если подмножество 
и определяется как множество упорядоченных пар 
, а его элементам нельзя дать однозначного ответа 
относительно свойства S о принадлежности к подмножеству 
, то есть характеристическая функция 
для 
принимает значения 
, то множество является нечетким.
Определение 3. Функция 
, принимающая значения в некотором упорядоченном множестве М (
) относительно свойства S и указывающая степень (уровень) принадлежности элемента к подмножеству А или , принимающая значения в некотором упорядоченном множестве М (
) относительно свойства S и указывающая степень (уровень) принадлежности элемента к подмножеству называется характеристической функцией принадлежности.
Определение 4. Пусть a Î [0,1]; Подмножеством a - уровня нечеткого подмножества называется обычное четкое множество Аa , где 
, "x Î E.
Понятие графа играет немаловажную роль в приложениях математики, поэтому стоит обобщить его на случай нечетких множеств.
Определение 5. Пусть существуют два множества Е1, Е2, причем x Î E1 у Î E2. Множество упорядоченных пар (x, y) определяет декартово произведение Е1, Ä Е2.
Нечеткое множество 
, такое, что "(x, y) Î Е1, Ä Е2: 
, где M – множество принадлежностей элементов множества Е1, Ä Е2, называется нечетким графом
Основные характеристики нечетких множеств и операции над нечеткими множествами, а также методы построения функций принадлежности подробно изложены в работе [1].
Постановка задачи. Применим теорию нечетких множеств для решения задачи диагностирования сложной технической системы.
Пусть объект диагностирования задан в виде нечеткого упорядоченного графа 
с n вершинами, где V и U - соответственно множества вершин и ребер. Вершинам графа ставятся в соответствие блоки объекта диагностирования, а ребрам - связи между блоками. Причем, связи между блоками обладают определенным уровнем устойчивости (степенью принадлежности) 
(
). Известно множество 
точек контроля, обусловленных назначением и конструкционным исполнением объекта диагностирования. Из множества 
выделяется подмножество 
. Каждой точке 
ставится в соответствие стоимость 
ее реализации. При этом задано число z дополнительно организуемых точек контроля. Требуется дополнить множество Y точек контроля множеством 
так, чтобы на множестве 
коэффициент глубины поиска дефекта любой кратности стремился к максимуму, а стоимость реализации назначенных точек контроля была минимальной.
Тогда математическая постановка задачи имеет вид:
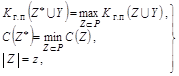, (1)
где 
значение стоимости реализации множества Z точек контроля объекта диагностирования.
Решение задачи. Рассматриваемая задача относится к классу многокритериальных задач. Для ее решения можно использовать метод свертывания векторного критерия, который подробно рассматривался в [2]. Этот метод оптимизации учитывает относительную важность частных критериев оптимальности с помощью построения скалярной функции F, являющейся обобщенным критерием оптимальности. Функция F с аддитивным критерием оптимальности имеет вид: 
, (2)
где 
-вектор частных критериев, причем 
соответствует нормированному коэффициенту глубины поиска дефекта любой кратности 
, 
- нормированной стоимости реализации дополнительных точек контроля 
; 
-весовые коэффициенты относительной важности частных критериев, которым при решении предлагается дать точные численные оценки.
Для нормирования частных критериев примем одинаковую шкалу измерения [a, b]. При этом [a, b]=[1, 2] для 
и [a, b]=[2, 1] для 
. В результате для нормирования получаем следующую формулу: 
=
. (3)
Для нормирования : 
=
. (4)
В результате задача сводится к решению однокритериальной задачи оптимизации:
=
=
, (6)
Полученная задача является задачей дискретной оптимизации, которую можно решить с помощью метода ветвей и границ.
Решение задачи для объекта диагностирования заданного в виде упорядоченного (четкого) графа G (V, U) подробно было рассмотрено в [3]. Отличительная особенность решения подобной задачи с использованием нечеткого упорядоченного графа в нахождении коэффициента глубины поиска дефекта любой кратности на определенном множестве точек контроля
Расчет коэффициента глубины поиска дефекта любой кратности с использованием нечетких множеств производится по [3]: Кгп = Fn(Y) / S, (7)
где Sn = 2n – 1, общее число возможных дефектов кратности от 1 до n, Fn(Y) - число однозначно различимых дефектов любой кратности на множестве точек контроля Y.
Определение 6. Дефект называется однозначно различимым на множестве точек контроля Y, если он обнаружим в системе без введения дополнительных точек контроля.
Рассматриваемый нечеткий упорядоченный граф можно представить в следующем виде: 
, при этом для решения поставленной задачи необходимо задать минимальный уровень устойчивости связи a (a-уровень) графа .
Далее для определения Fn(Y) будем использовать следующий алгоритм:
1) По графу строим матрицу достижимости D, исходя из правил построения пути в нечетком конечном графе [1].
2) Cтроим матрицу проверок 
, элементы которой представляют из себя нечеткое множество Для того, чтобы получить множество, определяющее вектор-строку матрицы проверок 
, необходимо в матрице достижимости взять нечеткое множество, определяемое строкой под номером i и нечеткое множество, определяемое столбцом под номером j, а затем найти их пересечение [1]. Таким образом строятся все вектор- строки матрицы проверок .
3) Определим матрицу B¢Y, которая будет содержать обычное (четкое) множество, состоящее из 0 и 1 и являющееся a - уровнем нечеткого множества матрицы (a - уровень или уровень устойчивости связи был определен заранее).
4) Из матрицы B¢Y вычеркиваем столбцы, состоящие только из нулей, в результате будет получена матрица BY.
5) В матрице BY выбираются столбцы, определяющие данный дефект.
6) Из матрицы BY вычеркиваются строки, которые не имеют единиц в выбранных столбцах, а затем вычеркиваются столбцы, имеющие единицы в этих строках.
7) Если из матрицы BY вычеркнуты все столбцы, кроме определяющих рассматриваемый дефект, тогда исследуемый дефект называется однозначно распознаваемым, в противном случае исследуемый дефект не является однозначно распознаваемым.
8) Подобным образом (п. 5-7) последовательно рассматриваем все предполагаемые дефекты. Количество однозначно распознаваемых дефектов определит Fn(Y).
Используя выше приведенный алгоритм и формулу (7) можно определить Кгп на любом множестве точек контроля и использовать для решения поставленной задачи.
Пример. В качестве примера многокритериальной оптимизации в задаче диагностики сложных технических систем рассмотрим объект, модель которого представлена в форме нечеткого упорядоченного графа (U, V) показанного на рис. 1.
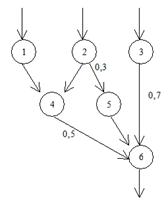
Рис. 1. Пример нечеткого упорядоченного графа
={((1,4)ï1),((2,4)ï1),((2,5)ï0,3),((3,6)ï0,7),((4,6)ï0,5),((5,6)ï1)}
Известно исходное множество Y = {6} точек контроля. Задано число z=2 дополнительно организуемых точек контроля, так же заданы стоимости реализации точек, претендующих на дополнительные точки контроля.
|
С1 |
С2 |
С3 |
С4 |
С5 |
|
5 ед. |
7 ед. |
6 ед. |
8 ед. |
4 ед. |
По графу построим матрицу достижимости D. На множестве Y = {6} построим матрицу проверок .
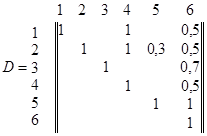
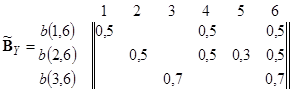
Определим величину общего числа возможных дефектов кратности от 1 до n (n= 6 )
Sn = 2n – 1 = 63
Определим минимальный уровень устойчивости связи (a-уровень) a = 0,5, и построим матрицу B¢Y. Исключим 5 столбец и получим матрицу BY
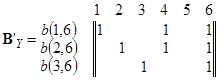
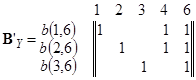
Используя вышеприведенный алгоритм по матрице BY рассматриваемого примера, получим следующие однозначно выявляемые дефекты:
b1, b2 , b3, b1Ú b3, b2Úb3. При этом Kгл (Y) = Fn(Y) / Sn = 5/ 63 = 0,079.
Из множества точек P = {1, 2, 3, 4} необходимо выбрать две точки, при которых Kгп максимален, а стоимость их реализации минимальна.
1-й шаг. За оценку на данном шаге принимаем выражение
. (8)
При этом YÈZ11 = {1, 6}, YÈZ12 = {2, 6}, YÈZ13 = {3, 6}, YÈZ14 = {4, 6}.
Определим Kгп (YÈZ1j) и NK(YÈZ1j) (
) для полученных множеств точек контроля, исходя из выше предложенных формул (7), (3).
Kгп (YÈZ11) = 0, 095; NK (YÈZ11) = 2; Kгп (YÈZ12) = 0, 095; NK (YÈZ12) = 2;
Kгп (YÈZ13) = 0, 079; NK (YÈZ13) = 1; Kгп (YÈZ14) = 0, 095; NK (YÈZ14) = 2.
Определим NC (Z1j), (), используя заданную стоимость реализации точек, претендующих на дополнительные точки контроля по формуле (4).
NC (Z11) = 1,75; NC (Z12) = 1,25; NC (Z13) = 1,5; NC (Z14) = 1.
Подставляя значения нормированных коэффициентов в выражение (8), определим значения обобщенных критериев оптимальности F (w, Q (YÈZ1j)) () ( F (w, Q (YÈZ11)) = = 1,93; F (w, Q (YÈZ12)) = 1,78; F (w, Q (YÈZ13)) = 1,15; F (w, Q (YÈZ14)) = 1,7; F (w, Q(YÈZ1)) = 1,93) и первой дополнительной точкой контроля является элемент, соответствующий вершине 1.
2-й шаг. За оценку на втором шаге принимаем выражение
, (9)
где YÈZ21 = {1, 2, 6}, YÈZ22 = {1, 3, 6}, YÈZ23 = {1, 4, 6}.
Для каждого из этих множеств определим Kгп (YÈZ2j), NK(YÈZ2j), NC (Z2j) (
) по формулам (7), (3), (4). Kгп (YÈZ21) = 0,143; NK (YÈZ21) = 2; NC (Z21) = 1; Kгп (YÈZ22) = 0,095; NK (YÈZ22) = 1;NC (Z22) = 1,33; Kгп (YÈZ23) = 0, 111; NK (YÈZ23) = 1,33;NC (Z23) = 2.
Определим значения обобщенных критериев оптимальности F(w, Q(YÈZ2j)) () по формуле (9) (F (w, Q (YÈZ21)) = 1,7; F (w, Q (YÈZ22)) = 1,1; F (w, Q (YÈZ23)) = 1,53; F (w, Q (YÈZ2)) = 1,7) и второй дополнительной точкой контроля назначаем элемент, определяемый вершиной 2.
Таким образом, для выполнения условия задачи должно быть следующее множеств точек контроля, YÈZ = {1, 2, 6}. При этом Kгп (YÈZ) = 0,14, Среал (Z) = 12 ед.
Заключение
Из сравнения решения задач, определение коэффициента глубины поиска дефекта любой кратности и стоимость введения дополнительных точек контроля для четкой задачи [2],[3],[6] и нечеткой задачи, рассмотренной в данной работе, видно, что решение задачи зависит от выбора уровня устойчивости связей a. Этот уровень зависит от величины некорректности внешнего воздействия на систему. При малых внешних воздействиях на техническую систему a®0 и задача становится более четкой. С повышением внешнего некорректного воздействия a®1 четкость задачи уменьшается. Так в приведенном примере при a=0,5 из рассмотрения выпадает целая ветвь системы. Для распознавания дефектов необходимо повышать число точек контроля. В связи с чем, значительно возрастает стоимость диагностических систем. В рассмотренной задаче коэффициент глубины поиска не велик, что оставляет возможность для появления случая когда дефекты не будут распознаны.
Приведенные в работе методы и алгоритмы обладают высокой степенью универсальности и могут быть использованы в любых областях науки и техники, где требуются надежная диагностика и контроль работоспособности технических объектов, систем или изделий подвергшихся некорректному внешнему воздействию.
Рецензенты:
Соколова Элеонора Станиславовна, доктор технических наук, профессор, зав. кафедрой «Информатика и системы управления», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е.Алексеева», г.Нижний Новгород.
Хранилов Валерий Павлович, доктор технических наук, доцент, профессор кафедры «Компьютерные технологии в проектировании и производстве», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е.Алексеева», г.Нижний Новгород.
Библиографическая ссылка
Бушуева М.Е., Беляков В.В., Макаров В.С., Колотилин В.Е. МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ КОНТРОЛЕПРИГОДНОСТИ ДИАГНОСТИЧЕСКИХ СИСТЕМ В УСЛОВИЯХ НЕЧЕТКОГО СОСТОЯНИЯ ОБЪЕКТА // Современные проблемы науки и образования. – 2012. – № 6. ;URL: https://science-education.ru/ru/article/view?id=7881 (дата обращения: 20.04.2024).